Find Minimum area ellipse enclosing a set of points in c++

Question

I have a set of 2D points. I need to find a minimum area ellipse enclosing all the points. Could someone give an idea of how the problem has to be tackled. For a circle it was simple. The largest distance between the center and the point. But for an ellipse its quite complicated which I do not know. I have to implement this in c++.

Larondalarosa

If there isn't a closed-form solution to this problem, it seems like it would be pretty amenable to some kind of heuristic search technique. – Adolphadolphe

Must the ellipse be centered at the origin? Must the ellipse's axes be parallel to the coordinate axes? (Any NO answer here would greatly complicate the problem.) – Deed

I have re-tag your question (why to tag JAVA when you clearly states you need C++?) – Uzia

JAVA was tagged unknowingly, – Larondalarosa

Is the center of the ellipse necessarily at (0,0) and the axes not rotated? If not, in the general case, you have the MVEE (minimum-volume enclosing ellipse) that gives the proper solution. – Madaras

Answer 1

These don't go as far as giving you C++ code, but they include in-depth discussion of effective algorithms for what you need to do.

https://www.cs.cornell.edu/cv/OtherPdf/Ellipse.pdf

http://www.stsci.edu/~RAB/Backup%20Oct%2022%202011/f_3_CalculationForWFIRSTML/Gaertner%20&%20Schoenherr.pdf

Morava

While linking to information which provides an answer is a useful input, StackOverflow prefers your answers to be of help in themselves. The idea is that an answer should at least contain a minimum summary of the solution so that it still has some value in case the links would die. – Splotch

Answer 2

The other answers here give approximation schemes or only provide links. We can do better.

Your question is addressed by the paper "Smallest Enclosing Ellipses -- Fast and Exact" by Gärtner and Schönherr (1997). The same authors provide a C++ implementation in their 1998 paper "Smallest Enclosing Ellipses -- An Exact and Generic Implementation in C++". This algorithm is implemented in a more usable form in CGAL here.

However, CGAL only provides the general equation for the ellipse, so we use a few transforms to get a parametric equation suitable for plotting.

All this is included in the implementation below.

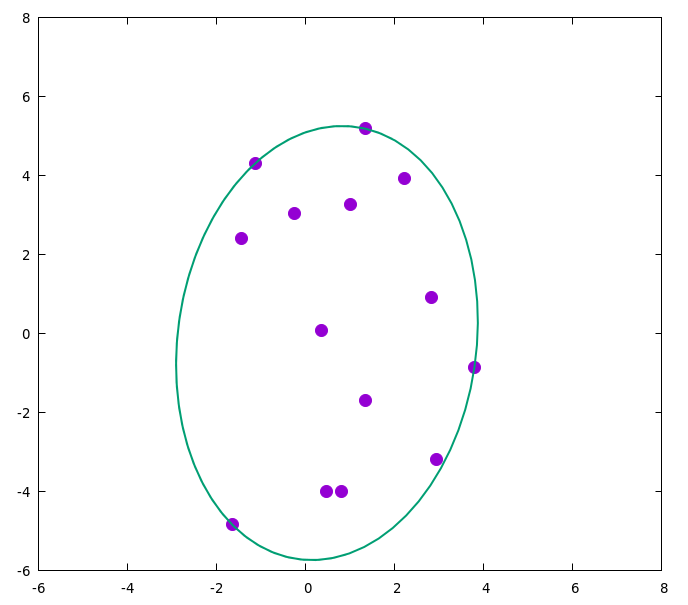
Using WebPlotDigitizer to extract your data while choosing arbitrary values for the lengths of the axes, but preserving their aspect ratio, gives:

-1.1314123177813773 4.316368664322679
1.345680085331649 5.1848164974519015
2.2148682495160603 3.9139687117291504
0.9938150357523803 3.2732678860664475
-0.24524315569075128 3.0455750009876343
-1.4493153715482157 2.4049282977126376
0.356472958558844 0.0699802473037554
2.8166270295895384 0.9211630387547896
3.7889384901038987 -0.8484766720657362
1.3457654169794182 -1.6996053411290646
2.9287101489353287 -3.1919219373444463
0.8080480385572635 -3.990389523169913
0.46847074625686425 -4.008682890214516
-1.6521060324734327 -4.8415723146209455

Fitting this using the program below gives:

a = 3.36286
b = 5.51152
cx = 0.474112
cy = -0.239756
theta = -0.0979706

We can then plot this with gnuplot

set parametric
plot "points" pt 7 ps 2, [0:2*pi] a*cos(t)*cos(theta) - b*sin(t)*sin(theta) + cx, a*cos(t)*sin(theta) + b*sin(t)*cos(theta) +
cy lw 2

to get

Implementation

The code below does this:

// Compile with clang++ -DBOOST_ALL_NO_LIB -DCGAL_USE_GMPXX=1 -O2 -g -DNDEBUG -Wall -Wextra -pedantic -march=native -frounding-math main.cpp -lgmpxx -lmpfr -lgmp

#include <CGAL/Cartesian.h>
#include <CGAL/Min_ellipse_2.h>
#include <CGAL/Min_ellipse_2_traits_2.h>
#include <CGAL/Exact_rational.h>

#include <cassert>
#include <cmath>
#include <fstream>
#include <iostream>
#include <string>
#include <vector>

typedef CGAL::Exact_rational             NT;
typedef CGAL::Cartesian<NT>              K;
typedef CGAL::Point_2<K>                 Point;
typedef CGAL::Min_ellipse_2_traits_2<K>  Traits;
typedef CGAL::Min_ellipse_2<Traits>      Min_ellipse;


struct EllipseCanonicalEquation {
  double semimajor; // Length of semi-major axis
  double semiminor; // Length of semi-minor axis
  double cx;        // x-coordinate of center
  double cy;        // y-coordinate of center
  double theta;     // Rotation angle
};

std::vector<Point> read_points_from_file(const std::string &filename){
  std::vector<Point> ret;

  std::ifstream fin(filename);
  float x,y;
  while(fin>>x>>y){
    std::cout<<x<<" "<<y<<std::endl;
    ret.emplace_back(x, y);
  }

  return ret;
}


// Uses "Smallest Enclosing Ellipses -- An Exact and Generic Implementation in C++"
// under the hood.
EllipseCanonicalEquation get_min_area_ellipse_from_points(const std::vector<Point> &pts){
  // Compute minimum ellipse using randomization for speed
  Min_ellipse  me2(pts.data(), pts.data()+pts.size(), true);
  std::cout << "done." << std::endl;

  // If it's degenerate, the ellipse is a line or a point
  assert(!me2.is_degenerate());

  // Get coefficients for the equation
  // r*x^2 + s*y^2 + t*x*y + u*x + v*y + w = 0
  double r, s, t, u, v, w;
  me2.ellipse().double_coefficients(r, s, t, u, v, w);

  // Convert from CGAL's coefficients to Wikipedia's coefficients
  // A*x^2 + B*x*y + C*y^2 + D*x + E*y + F = 0
  const double A = r;
  const double B = t;
  const double C = s;
  const double D = u;
  const double E = v;
  const double F = w;

  // Get the canonical form parameters
  // Using equations from https://en.wikipedia.org/wiki/Ellipse#General_ellipse
  const auto a = -std::sqrt(2*(A*E*E+C*D*D-B*D*E+(B*B-4*A*C)*F)*((A+C)+std::sqrt((A-C)*(A-C)+B*B)))/(B*B-4*A*C);
  const auto b = -std::sqrt(2*(A*E*E+C*D*D-B*D*E+(B*B-4*A*C)*F)*((A+C)-std::sqrt((A-C)*(A-C)+B*B)))/(B*B-4*A*C);
  const auto cx = (2*C*D-B*E)/(B*B-4*A*C);
  const auto cy = (2*A*E-B*D)/(B*B-4*A*C);
  double theta;
  if(B!=0){
    theta = std::atan(1/B*(C-A-std::sqrt((A-C)*(A-C)+B*B)));
  } else if(A<C){
    theta = 0;
  } else { //A>C
    theta = M_PI;
  }

  return EllipseCanonicalEquation{a, b, cx, cy, theta};
}


int main(int argc, char** argv){
  if(argc!=2){
    std::cerr<<"Provide name of input containing a list of x,y points"<<std::endl;
    std::cerr<<"Syntax: "<<argv[0]<<" <Filename>"<<std::endl;
    return -1;
  }

  const auto pts = read_points_from_file(argv[1]);

  const auto eq = get_min_area_ellipse_from_points(pts);

  // Convert canonical equation for rotated ellipse to parametric based on:
  // https://math.stackexchange.com/a/2647450/14493
  std::cout << "Ellipse has the parametric equation " << std::endl;
  std::cout << "x(t) = a*cos(t)*cos(theta) - b*sin(t)*sin(theta) + cx"<<std::endl;
  std::cout << "y(t) = a*cos(t)*sin(theta) + b*sin(t)*cos(theta) + cy"<<std::endl;
  std::cout << "with" << std::endl;

  std::cout << "a = " << eq.semimajor << std::endl;
  std::cout << "b = " << eq.semiminor << std::endl;
  std::cout << "cx = " << eq.cx << std::endl;
  std::cout << "cy = " << eq.cy << std::endl;
  std::cout << "theta = " << eq.theta << std::endl;

  return 0;
}

Rohde

Answer 3

Not sure if I can prove it, but it seems to me that the optimal solution would be characterized by tangenting (at least) 3 of the points, while all the other points are inside the ellipse (think about it!). So if nothing else, you should be able to brute force it by checking all ~n^3 triplets of points and checking if they define a solution. Should be possible to improve on that by removing all points that would have to be strictly inside any surrounding ellipse, but I'm not sure how that could be done. Maybe by sorting the points by x and y coordinates and then doing something fancy.

Not a complete solution, but it's a start.

EDIT: Unfortunately 3 points aren't enough to define an ellipse. But perhaps if you restrict it to the ellipse of the smallest area tangenting 3 points?

Perrault

Answer 4

as Rory Daulton suggest you need to clearly specify the constraints of solution and removal of any will greatly complicates things. For starters assume this for now:

• it is 2D problem
• ellipse is axis aligned
• center is arbitrary instead of (0,0)

I would attack this as standard genere and test problem with approximation search (which is hybrid between binary search and linear search) to speed it up (but you can also try brute force from start so you see if it works).

1. compute constraints of solution

   To limit the search you need to find approximate placement position and size of the ellipse. For that you can use out-scribed circle for your points. It is clear that ellipse area will be less or equal to the circle and placement will be near by. The circle does not have to be necessarily the smallest one possible so we can use for example this:

   1. find bounding box of the points
   2. let the circle be centered to that bounding box and with radius be the max distance from its center to any of the points.

   This will be O(n) complexity where n is number of your points.

2. search "all" the possible ellipses and remember best solution

   so we need to find ellipse center (x0,y0) and semi-axises rx,ry while area = M_PI*rx*ry is minimal. With approximation search each variable has factor of O(log(m)) and each iteration need to test validity which is O(n) so final complexity would be O(n.log^4(m)) where m is average number of possible variations of each search parameter (dependent on accuracy and search constraints). With simple brute search it would be O(n.m^4) which is really scary especially for floating point where m can be really big.

   To speed this up we know that the area of ellipse will be less then or equal to area of found circle so we can ignore all the bigger ellipses. The constrains to rx,ry can be derived from the aspect ratio of the bounding box +/- some reserve.

Here simple small C++ example using that approx class from link above:

//---------------------------------------------------------------------------
// input points
const int n=15; // number of random points to test
float pnt[n][2];
// debug bounding box
float box_x0,box_y0,box_x1,box_y1;
// debug outscribed circle
float circle_x,circle_y,circle_r;
// solution ellipse
float ellipse_x,ellipse_y,ellipse_rx,ellipse_ry;
//---------------------------------------------------------------------------
void compute(float x0,float y0,float x1,float y1) // cal with bounding box where you want your points will be generated
    {
    int i;
    float x,y;
    // generate n random 2D points inside defined area
    Randomize();
    for (i=0;i<n;i++)
        {
        pnt[i][0]=x0+(x1-x0)*Random();
        pnt[i][1]=y0+(y1-y0)*Random();
        }
    // compute bounding box
    x0=pnt[0][0]; x1=x0;
    y0=pnt[0][1]; y1=y0;
    for (i=0;i<n;i++)
        {
        x=pnt[i][0]; if (x0>x) x0=x; if (x1<x) x1=x;
        y=pnt[i][1]; if (y0>y) y0=y; if (y1<y) y1=y;
        }
    box_x0=x0; box_x1=x1;
    box_y0=y0; box_y1=y1;
    // "outscribed" circle
    circle_x=0.5*(x0+x1);
    circle_y=0.5*(y0+y1);
    circle_r=0.0;
    for (i=0;i<n;i++)
        {
        x=pnt[i][0]-circle_x; x*=x;
        y=pnt[i][1]-circle_y; y*=y; x+=y;
        if (circle_r<x) circle_r=x;
        }
    circle_r=sqrt(circle_r);
    // smallest area ellipse

    int N;
    double m,e,step,area;
    approx ax,ay,aa,ab;
    N=3; // number of recursions each one improves accuracy with factor 10
    area=circle_r*circle_r; // solution will not be bigger that this
    step=((x1-x0)+(y1-y0))*0.05; // initial position/size step for the search as 1/10 of avg bounding box size
    for (ax.init(         x0,          x1,step,N,&e);!ax.done;ax.step())    // search x0
    for (ay.init(         y0,          y1,step,N,&e);!ay.done;ay.step())    // search y0
    for (aa.init(0.5*(x1-x0),2.0*circle_r,step,N,&e);!aa.done;aa.step())    // search rx
    for (ab.init(0.5*(y1-y0),2.0*circle_r,step,N,&e);!ab.done;ab.step())    // search ry
        {
        e=aa.a*ab.a;
        // is ellipse outscribed?
        if (aa.a>=ab.a)
            {
            m=aa.a/ab.a; // convert to circle of radius rx
            for (i=0;i<n;i++)
                {
                x=(pnt[i][0]-ax.a);   x*=x;
                y=(pnt[i][1]-ay.a)*m; y*=y;
                // throw away this ellipse if not
                if (x+y>aa.a*aa.a) { e=2.0*area; break; }
                }
            }
        else{
            m=ab.a/aa.a; // convert to circle of radius ry
            for (i=0;i<n;i++)
                {
                x=(pnt[i][0]-ax.a)*m; x*=x;
                y=(pnt[i][1]-ay.a);   y*=y;
                // throw away this ellipse if not
                if (x+y>ab.a*ab.a) { e=2.0*area; break; }
                }
            }
         }

    ellipse_x =ax.aa;
    ellipse_y =ay.aa;
    ellipse_rx=aa.aa;
    ellipse_ry=ab.aa;
    }
//---------------------------------------------------------------------------

Even this simple example with only 15 points took around 2 seconds to compute. You can improve performance by adding heuristics like test only areas lower then circle_r^2 etc, or better select solution area with some math rule. If you use brute force instead of approximation search that expect the computation time could be even minutes or more hence the O(scary)...

Beware this example will not work for any aspect ratio of the points as I hardcoded the upper bound for rx,ry to 2.0*circle_r which may not be enough. Instead you can compute the upper bound from aspect ratio of the points and or condition that rx*ry<=circle_r^2...

There are also other ("faster") methods for example variation of CCD (cyclic coordinate descend) can be used. But such methods usually can not guarantee that optimal solution will be found or any at all ...

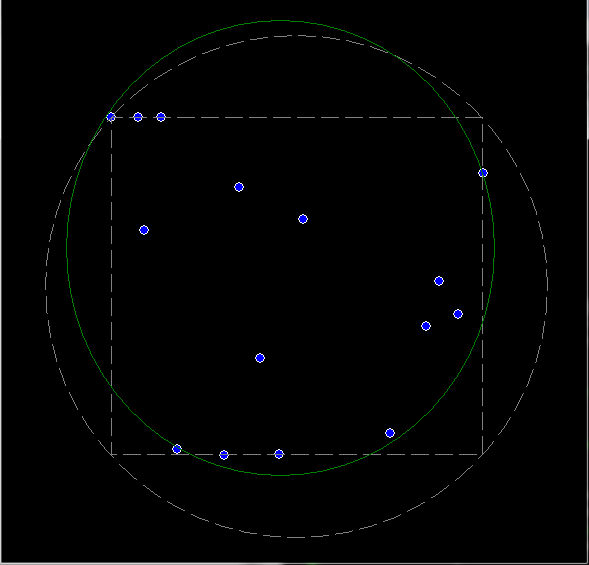
Here overview of the example output:

The dots are individual points from pnt[n], the gray dashed stuff are bounding box and used out-scribed circle. The green ellipse is found solution.

Uzia

Thank you for the help. It will take me some time to understand the code since I'm very new to C++. Also could you suggest me which libraries have to be used so that the code works. – Larondalarosa

@Larondalarosa only math.h and the approx class from the linked answer which you can directly copy to your source. – Uzia

Answer 5

Code for MVEE (minimal volume enclosing ellipse) can be found here, and works even for non-centered and rotated ellipses:

https://github.com/chrislarson1/MVEE

My related code:

bool _mvee(const std::vector<cv::Point> & contour, cv::RotatedRect & ellipse, const float epsilon, const float lmc) {
std::vector<cv::Point> hull;
cv::convexHull(contour, hull);

mvee::Mvee B;
std::vector<std::vector<double>> X;
// speedup: the mve-ellipse on the convex hull should be the same theoretically as the one on the entire contour
for (const auto &points : hull) {
    std::vector<double> p = {double(points.x), double(points.y)};
    X.push_back(p);   // speedup: the mve-ellipse on part of the points (e.g. one every 4) should be similar
}

B.compute(X, epsilon, lmc);   // <-- call to the MVEE algorithm

cv::Point2d center(B.centroid()[0], B.centroid()[1]);
cv::Size2d size(B.radii()[0] * 2, B.radii()[1] * 2);
float angle = asin(B.pose()[1][0]) * 180 / CV_PI;
if (B.pose()[0][0] < 0) angle *= -1;
ellipse = cv::RotatedRect(center, size, angle);
if (std::isnan(ellipse.size.height)) {
    LOG_ERR("pupil with nan size");
    return false;
}
return true;
}

Madaras