I have implemented 4 query algorithms with real-world data. All algorithms are don't require new data structures, or updates when marking an entry.
The test uses real-world data, with 40'000 nodes, and for each node tries to find a connection to 200 other random nodes. I expect that with more data, the results will be similar, because I expect that the "shape" of the data is very similar. For this experiment, I report the minimum, maximum, and average number of nodes read for each check.
- Depth-first search: min: 1, max: 1659, avg: 4.03
- Breath-first search: min: 1, max: 1659, avg: 4.02
- Reverse breath-first search: min: 1, max: 102859, avg: 4.21
- Bidirectional adaptive breath-first search: min: 1, max: 174, avg: 1.29
The best algorithm is 3.11 times faster than breath-first search (BFS). Reverse BFS is slower than BFS, due to the "shape" of the data: It seems each node references at most a few children. But there are a few nodes that are referenced by a lot of other nodes. So reverse search can be slow (max is much higher for reverse BFS).
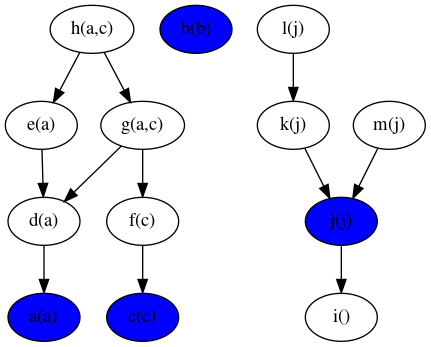
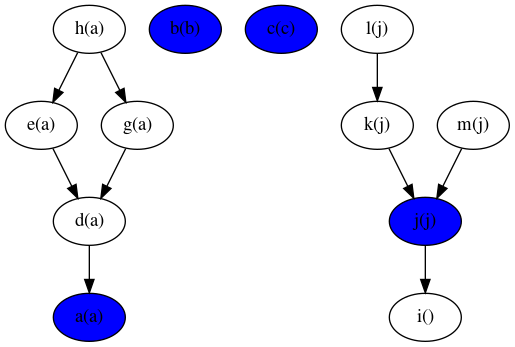
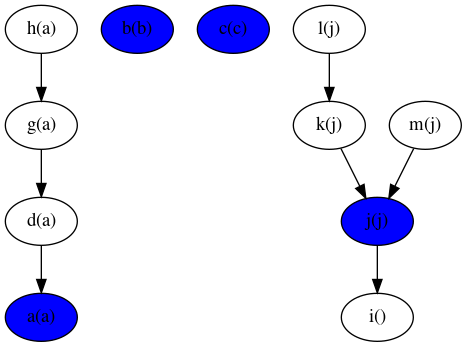
Bidirectional adaptive BFS uses the following algorithm:
- The idea is to do a mix of BFS and reverse BFS, in a balanced way.
- We use a mix of downward search (source to target), and upward search (target to source).
- We remember the nodes we have seen so far in both directions.
- At each step, we either expand downwards, or upwards.
- Which direction we go at each step depends on how many nodes we have seen in the last step on the way down, versus on the way up: If we have seen more on the way down, then the next step is to go up. Otherwise, go down.
Implementation (Java):
System.out.println("Number of nodes: " + nodes.size());
System.out.println();
int dfsCount = 0, bfsCount = 0, revCount = 0, biCount = 0;
int dfsMin = Integer.MAX_VALUE, bfsMin = Integer.MAX_VALUE, revMin = Integer.MAX_VALUE, biMin = Integer.MAX_VALUE;
int dfsMax = Integer.MIN_VALUE, bfsMax = Integer.MIN_VALUE, revMax = Integer.MIN_VALUE, biMax = Integer.MIN_VALUE;
int totalCount = 0;
Random r = new Random(1);
for (int i = 0; i < nodeList.size(); i++) {
int a = i;
for (int j = 0; j < 200; j++) {
int b;
do {
b = r.nextInt(nodes.size());
} while (a == b);
Node na = nodeList.get(a);
Node nb = nodeList.get(b);
totalCount++;
AtomicInteger x = new AtomicInteger();
boolean r1 = depthFirstSearch(x, na, nb);
dfsCount += x.get();
dfsMin = Math.min(dfsMin, x.get());
dfsMax = Math.max(dfsMax, x.get());
x.set(0);
boolean r2 = breathFirstSearch(x, na, nb);
bfsCount += x.get();
bfsMin = Math.min(bfsMin, x.get());
bfsMax = Math.max(bfsMax, x.get());
x.set(0);
boolean r3 = reverseBreathFirstSearch(x, na, nb);
revCount += x.get();
revMin = Math.min(revMin, x.get());
revMax = Math.max(revMax, x.get());
x.set(0);
boolean r4 = bidirectionalAdaptiveBFS(x, na, nb);
biCount += x.get();
biMin = Math.min(biMin, x.get());
biMax = Math.max(biMax, x.get());
x.set(0);
if (r1 != r2 || r1 != r3 || r1 != r4) {
depthFirstSearchTrace(na, nb);
bidirectionalAdaptiveBFS(x, na, nb);
throw new AssertionError(r1 + " " + r2 + " " + r3 + " " + r4);
}
}
}
System.out.println("Depth-first search");
System.out.printf("min: %d, max: %d, avg: %2.2f\n", dfsMin, dfsMax, ((double) dfsCount / totalCount));
System.out.println();
System.out.println("Breath-first search");
System.out.printf("min: %d, max: %d, avg: %2.2f\n", bfsMin, bfsMax, ((double) bfsCount / totalCount));
System.out.println();
System.out.println("Reverse breath-first search");
System.out.printf("min: %d, max: %d, avg: %2.2f\n", revMin, revMax, ((double) revCount / totalCount));
System.out.println();
System.out.println("Bidirectional adaptive breath-first search");
System.out.printf("min: %d, max: %d, avg: %2.2f\n", biMin, biMax, ((double) biCount / totalCount));
System.out.println();
static boolean depthFirstSearch(AtomicInteger count, Node source, Node target) {
HashSet<Node> tested = new HashSet<>();
tested.add(source);
return depthFirstSearch(count, tested, source, target);
}
static boolean depthFirstSearch(AtomicInteger count, HashSet<Node> tested, Node source, Node target) {
count.incrementAndGet();
for(Node n : source.references) {
if (n == target) {
return true;
}
if (!tested.contains(n)) {
tested.add(n);
if (depthFirstSearch(count, n, target)) {
return true;
}
}
}
return false;
}
static boolean breathFirstSearch(AtomicInteger count, Node source, Node target) {
HashSet<Node> tested = new HashSet<>();
tested.add(source);
return breathFirstSearch(count, tested, source, target);
}
static boolean breathFirstSearch(AtomicInteger count, HashSet<Node> tested, Node source, Node target) {
count.incrementAndGet();
for(Node n : source.references) {
if (n == target) {
return true;
}
}
for(Node n : source.references) {
if (!tested.contains(n)) {
tested.add(n);
if (breathFirstSearch(count, n, target)) {
return true;
}
}
}
return false;
}
static boolean reverseBreathFirstSearch(AtomicInteger count, Node source, Node target) {
HashSet<Node> tested = new HashSet<>();
tested.add(target);
return reverseBreathFirstSearch(count, tested, source, target);
}
static boolean reverseBreathFirstSearch(AtomicInteger count, HashSet<Node> tested, Node source, Node target) {
count.incrementAndGet();
for(Node n : target.referencedBy) {
if (n == source) {
return true;
}
}
for(Node n : target.referencedBy) {
if (!tested.contains(n)) {
tested.add(n);
if (breathFirstSearch(count, source, n)) {
return true;
}
}
}
return false;
}
static boolean bidirectionalAdaptiveBFS(AtomicInteger count, Node source, Node target) {
HashSet<Node> allSources = new HashSet<>();
HashSet<Node> sources = new HashSet<>();
allSources.add(source);
sources.add(source);
HashSet<Node> allTargets = new HashSet<>();
HashSet<Node> targets = new HashSet<>();
allTargets.add(target);
targets.add(target);
return bidirectionalAdaptiveBFS(count, allSources, allTargets, sources, targets);
}
static boolean bidirectionalAdaptiveBFS(AtomicInteger count, Set<Node> allSources, Set<Node> allTargets, Set<Node> sources, Set<Node> targets) {
while (!sources.isEmpty() && !targets.isEmpty()) {
if (sources.size() <= targets.size()) {
HashSet<Node> newSources = new HashSet<>();
for(Node source: sources) {
count.incrementAndGet();
for(Node n : source.references) {
if (!allSources.contains(n)) {
newSources.add(n);
allSources.add(n);
if (allTargets.contains(n)) {
return true;
}
}
}
}
sources = newSources;
} else {
HashSet<Node> newTargets = new HashSet<>();
for(Node target: targets) {
count.incrementAndGet();
for(Node n : target.referencedBy) {
if (!allTargets.contains(n)) {
newTargets.add(n);
allTargets.add(n);
if (allSources.contains(n)) {
return true;
}
}
}
}
targets = newTargets;
}
}
return false;
}
static class Node {
String name;
HashSet<Node> references = new HashSet<>();
HashSet<Node> referencedBy = new HashSet<>();
boolean marked;
Node(String name) {
this.name = name;
}
void addReference(Node n) {
references.add(n);
n.referencedBy.add(this);
}
public String toString() {
return name;
}
@Override
public boolean equals(Object other) {
if (!(other instanceof Node)) {
return false;
}
return name.equals(((Node) other).name);
}
@Override
public int hashCode() {
return name.hashCode();
}
}

$inof 1000 records. This should be much faster than doing 1000 reads. And now you can do the recursive logic outside of mongo, streaming queries back and forth. Honestly if I couldn't get rid of MongoDB, this is what I would try. – AdaptableO(n^5)! (Later, very carefully, improved toO(n^3). But reads wereO(log(n)).) – Adaptable