Detect if two line segments intersect using Cramer

I have used the code that has been posted here. Here is the code again:

from __future__ import division 

def line(p1, p2):
    A = (p1[1] - p2[1])
    B = (p2[0] - p1[0])
    C = (p1[0]*p2[1] - p2[0]*p1[1])
    return A, B, -C

def intersection(L1, L2):
    D  = L1[0] * L2[1] - L1[1] * L2[0]
    Dx = L1[2] * L2[1] - L1[1] * L2[2]
    Dy = L1[0] * L2[2] - L1[2] * L2[0]
    if D != 0:
        x = Dx / D
        y = Dy / D
        return x,y
    else:
        return False

# Usage
L1 = line([0,1], [2,3])
L2 = line([2,3], [0,4])

R = intersection(L1, L2)
if R:
    print "Intersection detected:", R
else:
    print "No single intersection point detected"

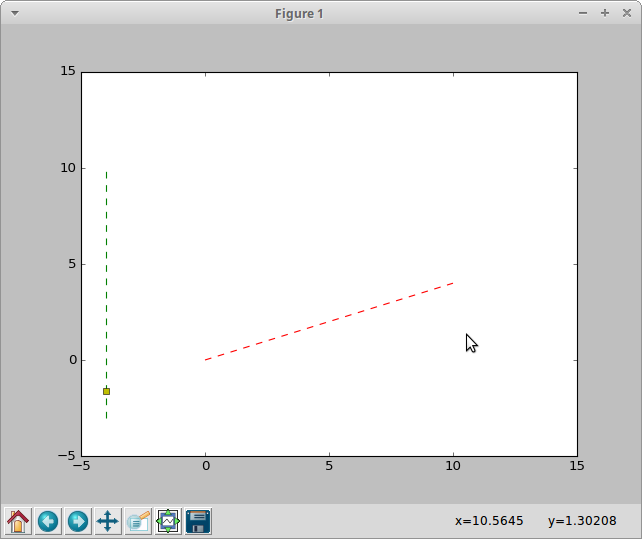
It implements the Cramer rule (adapted for lines; if determinant of the linear equation built for two given lines is 0 then the lines are not intersecting). However the problem I'm having with it is that it also detects intersections that are a result of the continuation of the two lines at hand. Here is a plot I've made using matplotlib which demonstrates the issue:

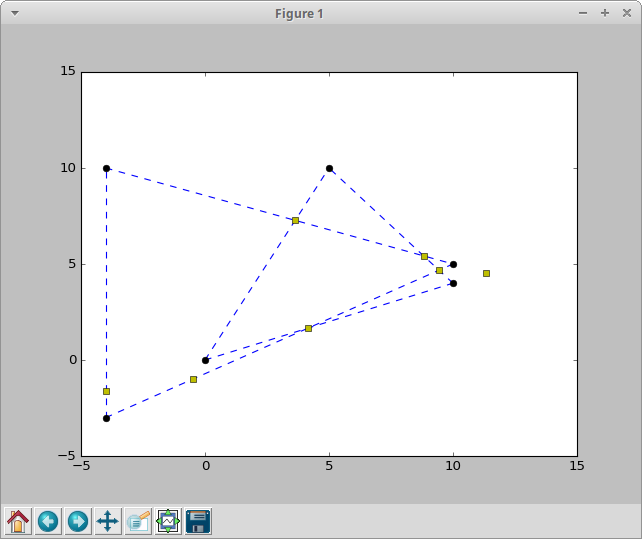
I also have a Triangle class which contains 3 Line objects and it demonstrates the issue even further since the class also has its own intersect(...) function which takes another triangle and checks which edges of both triangles are intersecting and where:

I want to detect line segment intersection using the algorithm from the link. The above line segments do not have an intersection. How do I do that?

I have two classes - Point and Line - that are used to work with these geometric elements in a more readable way. I have maintained the above script and wrapped around it (see Line.intersect(...)):

class Point:
  def __init__(self, x, y, z):
        self.x = x
        self.y = y
        self.z = z

  # Override __add__, __sub__ etc. to allow arithmetic operations with Point objects
  # ...

class Line:
  def __init__(self, p1, p2):
        self.p1 = p1
        self.p2 = p2
  # ...
  def intersect(self, l):
        def line(p1, p2):
            A = (p1.y - p2.y)
            B = (p2.x - p1.x)
            C = (p1.x*p2.y - p2.x*p1.y)
            return A, B, -C

        L1 = line(self.p1, self.p2)
        L2 = line(l.p1, l.p2)

        D  = L1[0]*L2[1] - L1[1]*L2[0]
        Dx = L1[2]*L2[1] - L1[1]*L2[2]
        Dy = L1[0]*L2[2] - L1[2]*L2[0]

        if D != 0:
            x = Dx / D
            y = Dy / D
            p = Point(x, y)
            return True, p

        return False, None

#Usage
l1 = Line(Point(0, 0), Point(10, 4))
l2 = Line(Point(-4, -3), Point(-4, 10))

res, p = l1.intersect(l2)
if not res:
    print('Lines don\'t intersect')
else:
    print('Lines intersect at [%f, %f]' % (p.x, p.y))

I'm also looking for an optimal (as in as few non-costly operations with as few memory footprint as possible) solution.

One possible solution is filtering out the resulted intersection points (the ones that are not part of both segments) by using Euclidean distance to determine if these points are lying on both segments or not. If not, then the intersection is a result of the continuation of one or both lines and should be considered invalid. This is however a costly operation and also involves taking all intersection points (no matter if point is part of both segments or not) into consideration.

UPDATE: I thought I have solved the problem but alas! the following has a problem. After looking closely to the comments I saw one made by @JerryCoffin who pointed out a possible duplicate with this post:

def intersect(self, l, contious=False):
        # Before anything else check if lines have a mutual abcisses
        interval_1 = [min(self.p1.x, self.p2.x), max(self.p1.x, self.p2.x)]
        interval_2 = [min(l.p1.x, l.p2.x), max(l.p1.x, l.p2.x)]
        interval = [
            min(interval_1[1], interval_2[1]),
            max(interval_1[0], interval_2[0])
        ]

        if interval_1[1] < interval_2[0]:
            print('No mutual abcisses!')
            return False, None

        # Try to compute interception
        def line(p1, p2):
            A = (p1.y - p2.y)
            B = (p2.x - p1.x)
            C = (p1.x*p2.y - p2.x*p1.y)
            return A, B, -C

        L1 = line(self.p1, self.p2)
        L2 = line(l.p1, l.p2)

        D  = L1[0]*L2[1] - L1[1]*L2[0]
        Dx = L1[2]*L2[1] - L1[1]*L2[2]
        Dy = L1[0]*L2[2] - L1[2]*L2[0]

        if D != 0:
            x = Dx / D
            y = Dy / D
            p = Point(x, y)
            if contiuous: # continuous parameter allows switching between line and line segment interception
                return True, p
            else:
                if p.x < interval[1] or p.x > interval[0]:
                    print('Intersection out of bound')
                    return False, None
                else:
                    return True, p
        else:
            print('Not intersecting')
            return False, None

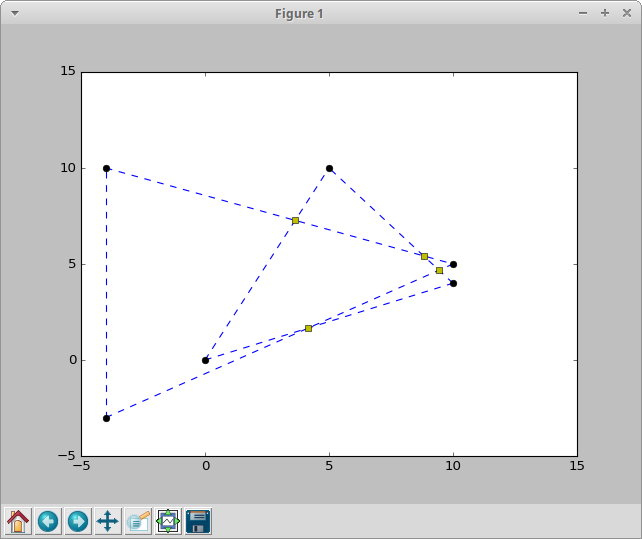
The result:

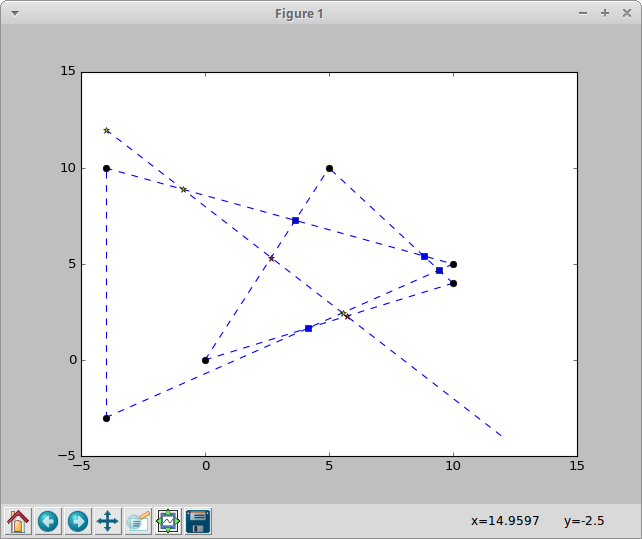
which looks nice and exactly what I want to have. However I added a line (the coordinates were more or less random but easy for me to check on the plot) namely Line(Point(-4, 12), Point(12, -4)). And imagine my surprise when I got yet again a single false positive:

As you can see there is an intersection detected at the top left corner at beginning of my line segment. It does indeed intersect with the continuation of the vertical line but not with the actual line segment. It seems that the fact that both line segments have the same x while the one being vertical poses an issue. So I'm still clueless how to solve the issue.

Recommended topics

Hot tags