How to find the "interior boundary" / "interior convex hull" for a list of 3D points?

Question

I need some help with writing this algorithm.

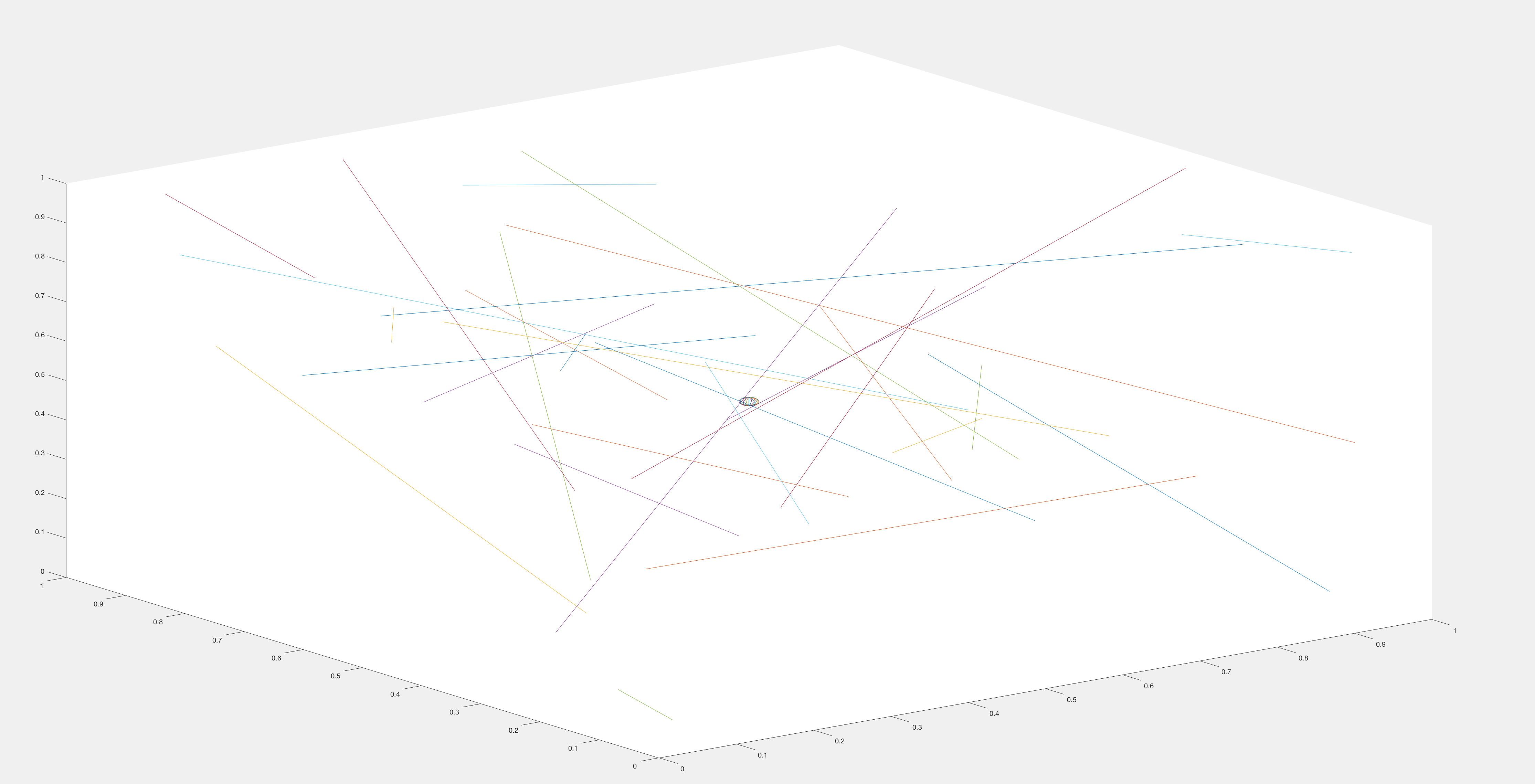
For a given set of lines in space, I am trying to find the accessible volume when the origin (reference point) is 0.5,0.5,0.5. Currently, I do the following:

For each line, calculate the distance to the origin (0.5,0.5,0.5). Then, gather all these perpendicular distance points on all the lines into a list.

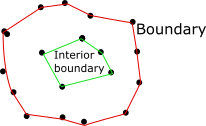
Now, I would like to calculate the "interior" (neither the boundary nor the convhull), because I want to evaluate the accessible volume for a ball centered at (0.5,0.5,0.5).

---

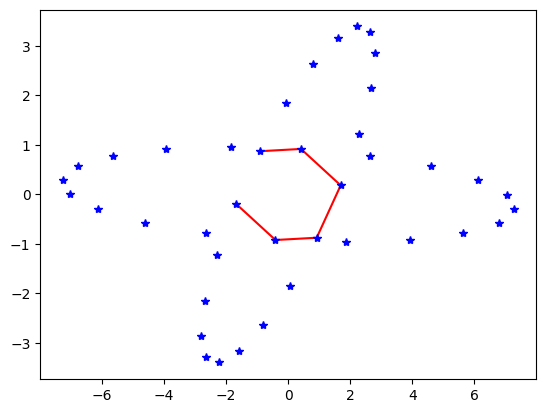
For example I would like to compute with my algorithm the green (internal line) in this simple example:

---

The configuration:

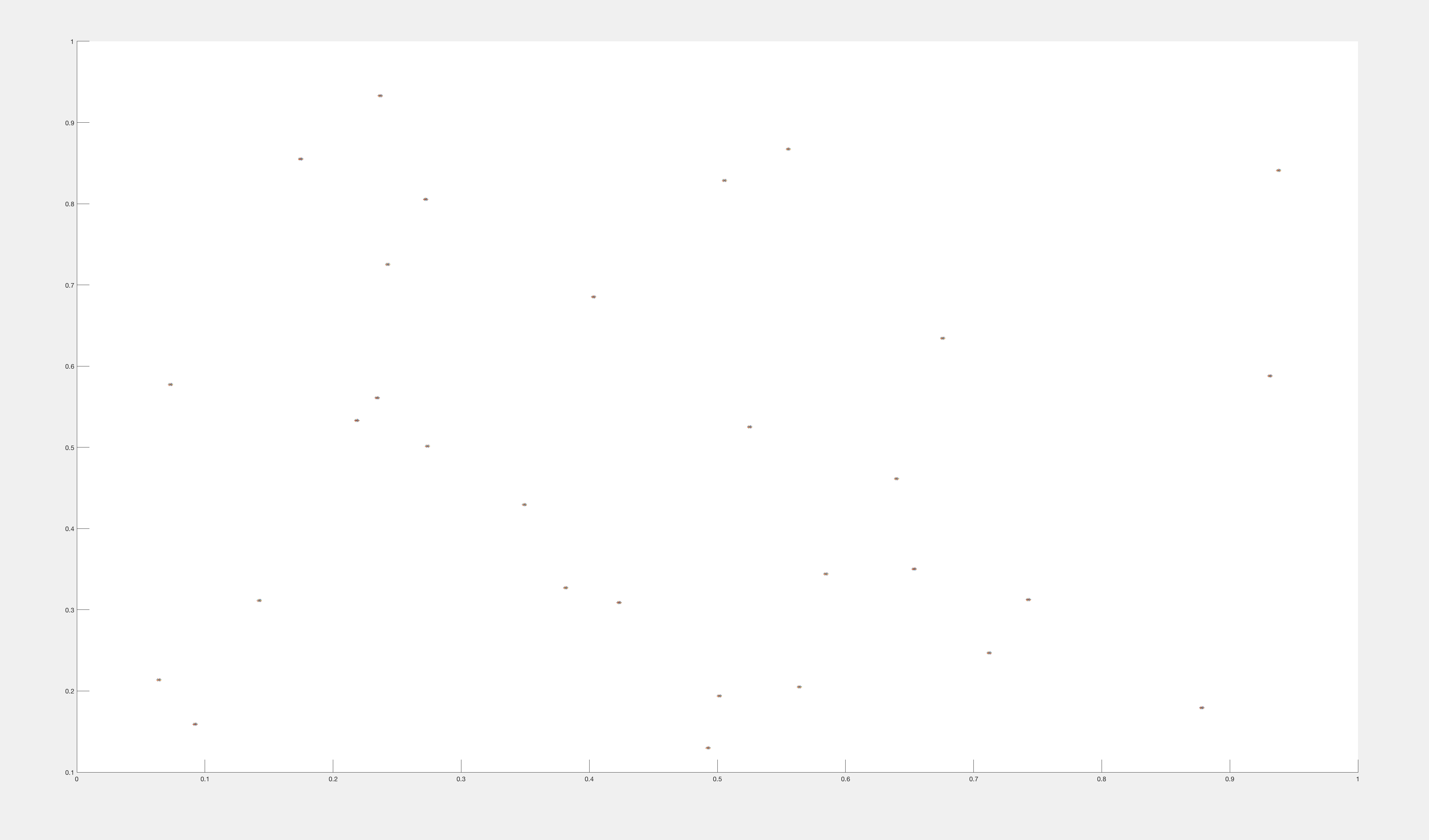
The closest points from the origin (0.5,0.5,0.5) to the lines

Only the points for whom I want the "internal boundary" be computed. Meaning the shape that bounds all the point either outside of the interior or on its boundary.

Here is the code for which I want something else rather than convhull:

close all
N=30;

S1 = cell(1, N);
for k = 1:N, S1{k} = rand(1, 3); end
S2 = cell(1, N);
for k = 1:N, S2{k} = rand(1, 3); end

M1 = cat(3, S1{:});
M2 = cat(3, S2{:});
M  = permute(cat(1, M1, M2), [1, 3, 2]);
figure
plot3(M(:, :, 1), M(:, :, 2), M(:, :, 3))
hold on
[x,y,z] = sphere;
x=x/100;y=y/100;z=z/100;
plot3(x+0.5,y+0.5,z+0.5)


figure 
hold on

NearestIntersectionPoints = cell(1,N); 
for k = 1:N 
    tmp1 = M(1,k,:); tmp2 = M(2,k,:);
    v1=tmp1(1,:); v2=tmp2(1,:);
    [d, intersection] = point_to_line([0.5,0.5,0.5], v1, v2);
    
    [x,y,z] = sphere;
    x=x/500;y=y/500;z=z/500;
    plot3(x+intersection(1),y+intersection(2),z+intersection(3))
    NearestIntersectionPoints{k} = intersection;

end


MHull = cat(3,NearestIntersectionPoints{:});
X=MHull(:,1,:); Y=MHull(:,2,:); Z=MHull(:,3,:);
X=X(:); Y=Y(:); Z=Z(:);
k = boundary(X,Y,Z);
hold on

plot3(X(k),Y(k),Z(k), 'r-*')


function [d,intersection] = point_to_line(pt, v1, v2)
      a = v1 - v2;
      b = pt - v2;
      d = norm(cross(a,b)) / norm(a);
      theta = asin(norm(cross(a,b))/(norm(a)*norm(b)));
      intersection = v2 + a * cos(theta);
      
end

Bonham

How do you define the interior space? As a ball? As the largest convex shape that fits inside the points? Something else? Hint-- the largest ball centered at your origin is trivial, the other is highly complex and, I believe, a O(N^7) problem. – Coronel

@CrisLuengo, I want the convex shape. The ball I guess is basically just to take the min distance to all the lines and plot a ball. Is there some mobious or any transformation that I can do on the data in order to find the internal convex hull? It's a similar problem to the convex hull just from inside. The thing is that even the Naive algorithm for this I can't figure out. – Bonham

Look for "convex skull". The power-7 order is is 2D, not sure if there's a 3D variant. – Coronel

@CrisLuengo I think you mean "convex hull". – Squeaky

@AlexisOlson no the convex hull gives the exterior boundary. I don't want that I want the convex hull from inside of the boundary. He's right. – Bonham

So you essentially want the interior of the convex hull? That is, the convex hull minus the boundary of the convex hull. – Squeaky

What do you mean by the boundary of the convex hull? If you mean to substructure this 2 it won't work. Image taken from here – Bonham

@AlexisOlson: Here is an "open problems" paper from the discrete geometry community about the convex skull problem: tc18.org/openProblems/convex_skull.pdf – Coronel

According to the link in my previous comment, the polygon with sides parallel to the axes is easier to obtain (O(N^2) in 2D). Would that suffice? – Coronel

@Bonham Boundary, interior, and convex hull are precisely defined mathematical terms (topology). I was referring to those definitions. I haven't figured out what exactly you're asking yet. – Squeaky

Can you draw some simplified diagrams that illustrate what you are after? (A minimal working example). – Squeaky

@AlexisOlson, see attached an example. – Bonham

@Spektre can you elaborate what exactly do you mean? – Bonham

@Spektre it's hard to tell. – Bonham

@Spektre the points are in a volume they are not on curved surface. – Bonham

@Bonham I have moved the comment into answer ... – Poniard

Answer 1

I would do it like this:

1. tetrahedronize your pointcloud

   so create a mesh consisting of tetrahedrons where no tetrahedron intersect any other or contain any point in it. I do it like this:

   1. structures

   you need list of points,triangles and tetrahedrons. Each triangle need one counter which will tell you if it is used once or twice.

   2. create first tetrahedron

   by 4 nested loops through all points and check if formed tetrahedron does not contain any point inside. If not stop as you found your first tetrahedron. This is O(n^5) but as there are a lot of valid tetrahedrons it will never reach such high runtime... Now just add this tetrahedron to triangle and tetrahedron lists.

   3. find next tetrahedron

   now loop through all triangles that has been used once. for each form tetrahedron by using those 3 points used by it and find 4th point the same way as in #2. Valid tetrahedron must not contain any points in it and also must not intersect any existing tetrahedron in the list.

   To ensure whole volume will be filled without holes you need to prioritize the process by preferring tetrahedrons with more triangles already in list. So first search 4 triangles if no found than 3 etc ...

   For each found valid tetrahedron add it to the lists and look again until no valid tetrahedron can be formed ... The whole process is around O(n^2) so be careful with too many points in pointcloud. Also having normals for triangles stored can speed the tests a lot ...

2. outer boundary

   outer boundary consist of triangles in list which have been used just once

3. interior boundary

   interior gap tetrahedrons should be larger than all the others. So check their size against average size and if bigger they are most likely a gap. So group them together to lists. Each gap have only large tetrahedrons and all of them must share at least one face (triangle). Now just count the triangle usage for each group alone and all the triangles used just once will form your gap/hole/interior boundary/mesh.

If your point density is uniform you can adapt this:

• Finding holes in 2d point sets?

And create a voxel map of point density... voxels with no density are either gap or outer space. This can be used for faster and better selection of interior tetrahedrons.

Poniard

Is it better if I use the actual lines instead of finding the nearest points? – Bonham

@Bonham I do not think so as in your plot the lines are quite big so you might end up with non-tetrahedronized areas – Poniard

I am a bit lost, I tried to implement your algorithm, but I am not sure how to actually write the first part of tetrahedronize your pointcloud – Bonham

@Bonham I do not code in Matlab so can not help you there but there is high possibility it got some package or function doing this. Try to find functions for mesh and or volume geometry. – Poniard

I meant if you can write a pseudo code more rigorously, the name of the algorithm to use in each step. No need to code for me. – Bonham

Because each step in your algorithm isn't any either from the original problem (unless you are aware of other algorithms I don't know). – Bonham

Answer 2

If I understand well your question, you want the largest volume inside another volume, without points in common between the two volumes.

The outer volume is built from a subset of the set of points. The obvious solution is to build the inner volume with the rest of points.

A volume from a set of points can be made in several ways. If the volume is not convex, then you need some more info (e.g. minimum angle between faces) because you get starred polytopo or cuasi-convex, or some other shape.

For convex volume I recomend the 3D Delaunay construction, with tetrahedra. The boundary is defined by the faces of "tets" that are not shared with other "tets".

Remove from the full set of points those belonging to the boundary: Each tet in boundary has a fourth point that does not lie on the boundary.

The inner volume is another Delaunay construction. Perhaps you only need the fourth points from the previous boundary-tets.

Frater

Answer 3

What I did in the end was something like that:

import numpy as np
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt

def plot_random_points_on_circles(N: int, R: list, center: list):
    """
    Generates two sets of N random points on two circles with radii R and centers at center.
    Scales the points and calculates the convex hull of the scaled points.
    Plots the convex hull and the original points.

    :param N: Number of points to generate on each circle
    :type N: int
    :param R: List of radii for the two circles
    :type R: list
    :param center: List of x and y coordinates for the center of the circles
    :type center: list
    """
    x = np.zeros((len(R), N))
    y = np.zeros((len(R), N))
    theta = np.linspace(0, 2 * np.pi, N + 1)
    theta = theta[:-1]

    for i in range(len(R)):
        x[i,:] = R[i] * (np.random.randn() + 1) * np.cos(theta + np.random.rand()) + center[0]
        y[i,:] = R[i] * (np.random.randn() + 1) * np.sin(theta + np.random.rand()) + center[1]

    x = np.concatenate((x[0,:], x[1,:]))
    y = np.concatenate((y[0,:], y[1,:]))
    rSquared = x**2 + y**2
    q = rSquared / max(rSquared)**2
    xx = x / q
    yy = y / q

    k = ConvexHull(np.column_stack((xx, yy)))
    plt.plot(x[k.vertices], y[k.vertices], 'r-', x, y, 'b*')
    plt.show()

N = 20
R = [2, 6]
center = [0, 0]

plot_random_points_on_circles(N, R, center)

Bonham