I know I can change frequency by whole numbers by changing the variable shift but how can I change the frequency using numbers with decimal places like .754 or 1.2345 or 67.456. If I change the variable 'shift' to a non-whole like number like 5.1 I get an error subscript indices must be either positive integers less than 2^31 or logicals from line mag2s = [mag2(shift+1:end), zeros(1,shift)];
Example Code below from question increase / decrease the frequency of a signal using fft and ifft in matlab / octave works with changing the variable shift (but it only works with whole numbers, I need it to work with decimals numbers also).
PS: I'm using octave 3.8.1 which is like matlab and I know I could change the frequency by adjusting the formula in the variable ya but ya will be a signal taken from an audio source (human speech) so it won't be an equation. The equation is just used to keep the example simple. And yes Fs is large due to the fact that signal files used are around 45 seconds long which is why I can't use resample because I get a out of memory error when used.
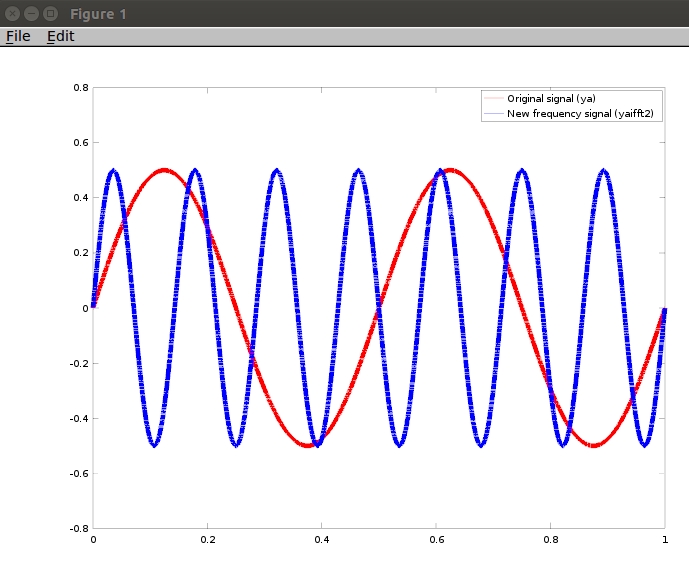
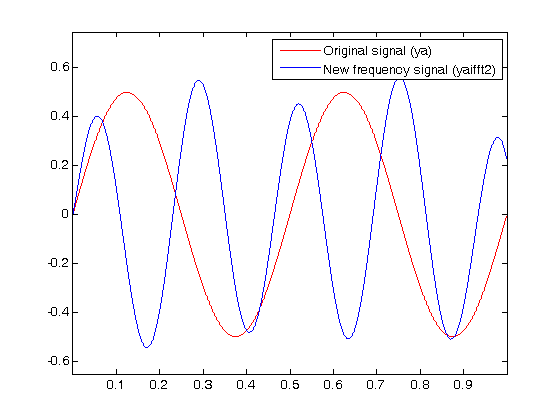
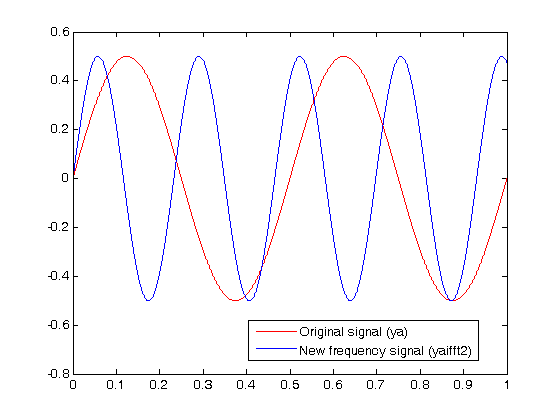
Here's a animated youtube video example of what I'm trying to get when I use the test equation ya= .5*sin(2*pi*1*t)+.2*cos(2*pi*3*t) and what I'm trying to get happen if I varied the variable shift from (0:0.1:5) youtu.be/pf25Gw6iS1U please keep in mind that ya will be an imported audio signal so I won't have an equation to easily adjust
clear all,clf
Fs = 2000000;% Sampling frequency
t=linspace(0,1,Fs);
%1a create signal
ya = .5*sin(2*pi*2*t);
%2a create frequency domain
ya_fft = fft(ya);
mag = abs(ya_fft);
phase = unwrap(angle(ya_fft));
ya_newifft=ifft(mag.*exp(i*phase));
% ----- changes start here ----- %
shift = 5; % shift amount
N = length(ya_fft); % number of points in the fft
mag1 = mag(2:N/2+1); % get positive freq. magnitude
phase1 = phase(2:N/2+1); % get positive freq. phases
mag2 = mag(N/2+2:end); % get negative freq. magnitude
phase2 = phase(N/2+2:end); % get negative freq. phases
% pad the positive frequency signals with 'shift' zeros on the left
% remove 'shift' components on the right
mag1s = [zeros(1,shift) , mag1(1:end-shift)];
phase1s = [zeros(1,shift) , phase1(1:end-shift)];
% pad the negative frequency signals with 'shift' zeros on the right
% remove 'shift' components on the left
mag2s = [mag2(shift+1:end), zeros(1,shift)];
phase2s = [phase2(shift+1:end), zeros(1,shift) ];
% recreate the frequency spectrum after the shift
% DC +ve freq. -ve freq.
magS = [mag(1) , mag1s , mag2s];
phaseS = [phase(1) , phase1s , phase2s];
x = magS.*cos(phaseS); % change from polar to rectangular
y = magS.*sin(phaseS);
yafft2 = x + i*y; % store signal as complex numbers
yaifft2 = real(ifft(yafft2)); % take inverse fft
plot(t,ya,'-r',t,yaifft2,'-b'); % time signal with increased frequency
legend('Original signal (ya) ','New frequency signal (yaifft2) ')