Approximate a curve with a limited number of line segments and arcs of circles

Question

Is there any algorithm that would allow to approximate a path on the x-y plane (i.e. an ordered suite of points defined by x and y) with a limited number of line segments and arcs of circles (constant curvature)? The resulting curve needs to be C1 (continuity of slope).

The maximum number or segments and arcs could be a parameter. An additional interesting constraint would be to prevent two consecutive circles of arcs without an intermediate line segment joining them.

I do not see any way to do this, and I do not think that there exists a method for it, but any hint towards this objective is welcome.

Example:

Sample file available here

Consider this path. It looks like a line, but is actually an ordered suite of very close points. There is no noise and the order of the sequence of points is well known.

I would like to approximate this curve with a minimum number of succession of line segments and circular arcs (let's say 10 line segments and 10 circular arcs) and a C1 continuity. The number of segments/arcs is not an objective itself but I need any parameter which would allow to reduce/increase this number to attain a certain simplicity of the parametrization, at the cost of accuracy loss.

Solution:

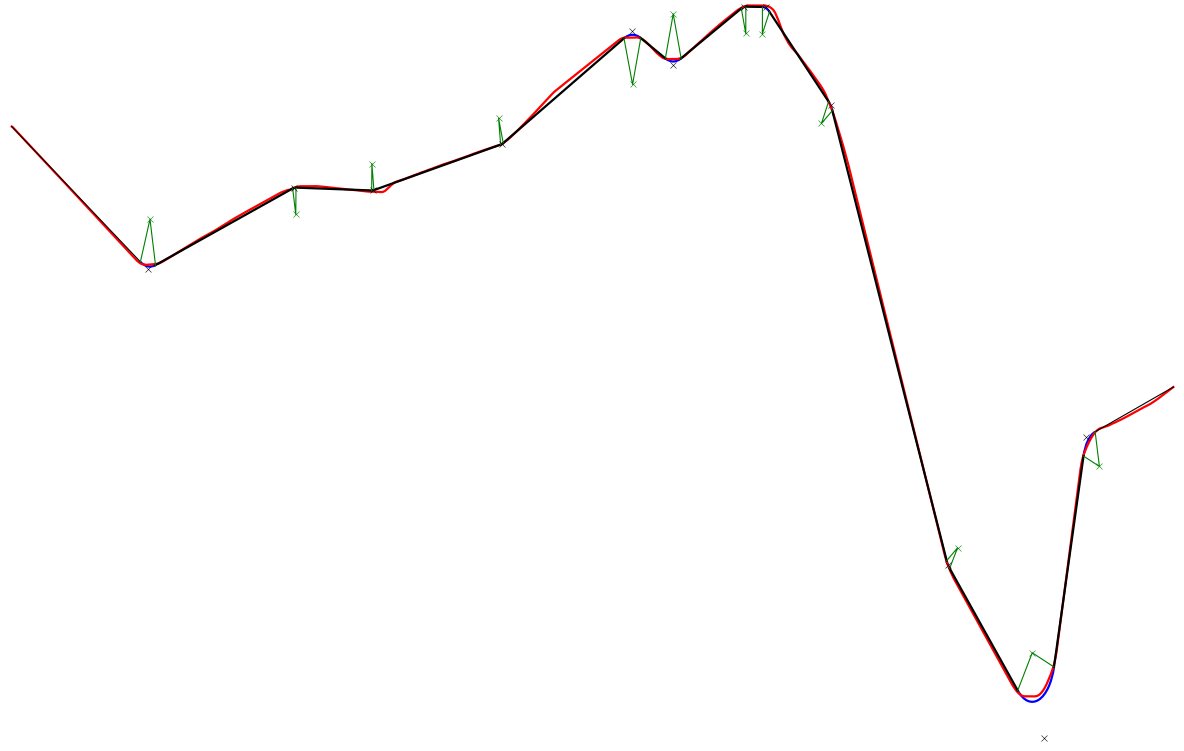
Here is my solution, based on Spektre's answer. Red curve is original data. Black lines are segments and blue curves are circle arcs. Green crosses are arc centers with radii shown and blue ones are points where segments potentially join.

1. Detect line segments, based on slope max deviation and segment minimal length as parameters. The slope of the new segment step is compared with the average step of the existing segment. I would prefer an optimization-based method, but I do not think that it exists for disjoint segments with unknown number, position and length.
2. Join segments with tangent arcs. To close the system, the radius is chosen such that the segments extremities are the least possible moved. A minimum radius constraint has been added for my purposes. I believe that there will be some special cases to treat in the inflexion points are far away when (e.g. lines are nearly parallel) and interact with neigboring segments.

Anson

raster or vector input? look for curve fitting without sample input/output is hard to recommend anything. My usual approach on vector form is to group sampled points with neighboars (connected components analysis) and then determine if they are lines or curves (based on angle change per distance) then join line subsegments together and fit the curves ... – Guthrun

Vector input: I modified the question to be more clear. The input is a suite of points defined by x and y. – Anson

Answer 1

the C1 requirement demands the you must have alternating straights and arcs. Also realize if you permit a sufficient number of segments you can trivially fit every pair of points with a straight and use a tiny arc to satisfy slope continuity.

I'd suggest this algorithm,

1 best fit with a set of (specified N) straight segments. (surely there are well developed algorithms for that.)

2 consider the straight segments fixed and at each joint place an arc. Treating each joint individually i think you have a tractable problem to find the optimum arc center/radius to satisfy continuity and improve the fit.

3 now that you are pretty close attempt to consider all arc centers and radii (segments being defined by tangency) as a global optimization problem. This of course blows up if N is large.

Eudemonism

Answer 2

so you got a point cloud ... for such Usually points close together are considered connected so:

1. you need to add info about what points are close to which ones

   points close only to 2 neighbors signaling interior of curve/line. Only one neighbor means endpoint of curve/lines and more then 2 means intersection or too close almost or parallel lines/curves. No neighbors means either noise or just a dot.

2. group path segments together

   This is called connected component analysis. So you need to form polylines from your neighbor info table.

3. detect linear path chunks

   these have the same slope among neighboring segments so you can join them to single line.

4. fit the rest with curves

Here related QAs:

• Finding holes in 2d point sets?
• Algorithms: Ellipse matching
• How approximation search works see the sublinks there are quite a bit of examples of fitting
• Trace a shape into a polygon of max n sides

[Edit1] simple line detection from #3 on your data

I used 5.0 deg angle change as threshold for lines and also minimal size fo detected line as 50 samples (too lazy to compute length assuming constant point density). The result looks like this:

dots are detected line endpoints, green lines are the detected lines and white "lines" are the curves so I do not see any problem with this approach for now.

Now the problem is with the points left (curves) I think there should be also geometric approach for this as it is just circular arcs so something like this

• Formula to draw arcs ending in straight lines, Y as a function of X, starting slope, ending slope, starting point and arc radius?

And this might help too:

• Circular approximation of polygon (or its part)

Guthrun

I added some details in the question to be more clear. I suppose only steps 3 and 4 are needed in my case. First detect linear path chunks, and then join the segments with curves. It will be needed to modify the segments extremities (prolongation/restriction) to maintain C1 continuity. – Anson

@Anson are you bound to circular arcs or can you use something better like elliptic arc or cubics ? – Guthrun

Only circular arcs and line segments. Ideally not 2 consecutive arcs. – Anson

@Anson you should share a sample test data in vector form for testing ... ideally in ASCII for easy access like SVG or custom ASCII dump. Which bullet is the problem ? – Guthrun

Step 3 is the issue: there are plenty of possibilities, and I am not sure that slope only is a sufficient criteria. Slope can vary significantly between 2 points, but if the distance between points is small this point may still be "sufficiently" aligned with a line segment. – Anson

@Anson small slope angle deviations are considered lines. But how to compute the slope angle is a different matter for big lines it is clear just use atan2 but for very small lines you need to interpolate with neighboring segments too or ignore them. That depends on what your goal is. For example my HW interpolators use detail parameter which is a smallest distance between points so if any segment is smaller it is joined with its neighbor... I think this apply to your case too as you are lowering the points number anyway. – Guthrun

Thanks, I could do a similar approach and get the curve showed in the edited question. – Anson

Answer 3

A typical constraint when approximating a given curve by some other curve is to bound the approximate curve to an epsilon-hose within the original curve (in terms if Minkowski sum with a disk of fixed radius epsilon).

For G1- or C2-continuous approximation (which people from CNC/CAD like) with biarcs (and a straight-line segment could be seen as an arc with infinite radius) former colleagues of mine developed an algorithm that gives solutions like this [click to enlarge]:

The above picture is taken from the project website: https://www.cosy.sbg.ac.at/~held/projects/apx/apx.html

The algorithm is fast, that is, it runs in O(n log n) time and is based on the generalized Voronoi diagram. However, it does not give an approximation with the exact minimum number of elements. If you look for the theoretical optimum I would refer to a paper by Drysdale et al., Approximation of an Open Polygonal Curve with a Minimum Number of Circular Arcs and Biarcs, CGTA, 2008.

Dirt

This is very close to what I need. I wish they had published the code. – Makings

Simply write Prof. Held, and maybe mention your purpose. – Dirt

Answer 4

I solved this problem using biarcs. Yes, it has been 5.5 years sinse OP. What are biarcs? Given 2 vectors in space (source+direction) you can connect them with 2 arcs. here is a C++ solution for finding biarcs for 2 3D vectors and more info about them.

Define the begginng of the polyline t=0 and the end of it t=1. The algo is iterative: create a biarc for t=0 to t=1 and check if the biarc is close enough to all of the points along the way. Also check that the biarc isn't straying too far from the polyline. If it does, you are finished.

Else split the polyline in half and check again for t=0 to t=0.5 and t=0.5 to t=1. If it fits, you're good, else split again. Repeat recursivly till the biarcs fit.

I want to publish my code opensource, but my company policy forbids for now.

Makings