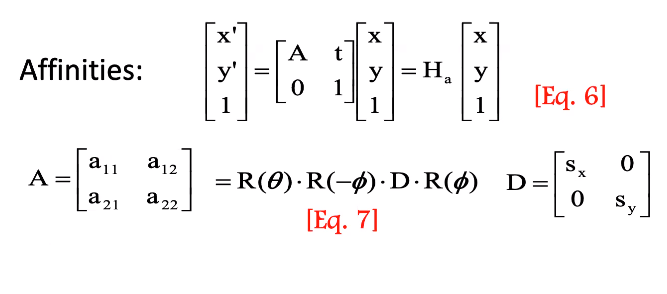what is anisotropic scaling in computer vision?

Question

What is anisotropic scaling? And how is it achieved w.r.t image processing and computer vision?

I understand that it is some form of non-uniform scaling as Wikipedia puts it, but I still don't get a good grasp of what it actually means when applied to images. Recently, some deep learning architectures like R-CNN for object detection also uses it but doesn't show much light on this topic.

Any examples and visual illustrations that explains the concept clearly would be really nice.

Ostosis

I have no domain knowledge, but linguistically "anisotropic" and "non-uniform" are synonymous. Based on this I imagine a linear transformation that is defined by a diagonal matrix the diagonals of which are unequal. Bit more generally, I'd guess that it's a linear transformation with two perpendicular eigenvectors and two non-equal eigenvalues. – Reconnoiter

Answer 1

Non-uniform scaling just means that different scales are applied to each dimension, making it anisotropic. The opposite would be isotropic scaling, where the same scale is applied to each dimension.

In the context of R-CNN, the authors did a trick to use variable sized images with the classification network, they resize any image into a fixed size (I believe it was 224x224), and this is done independently of the aspect ratio of the image. So say you have a 1280x720 image, and if it is resized to 224x244, then the scales are 1280/224 and 720/224, which obviously are not the same, hence anisotropic scaling.

Iveson

Could you please add a bit more information on this? Some visual illustrations would be great! – Ostosis

Answer 2

@kmario23 in the context of CV and CG, a nice example is an Affinity Transformation https://web.stanford.edu/class/cs231a/

Different from a Similarities Transformation, where we have an isotropic scaling. But the D is an example of Anisotropic scaling since s_x is different from s_y.

$$
\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}
$$

 Instead for an isotropic scaling  we would have

$$
\begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix}
$$

If you are looking for images I would recommend this presentation [ Michael Bronstein.] https://slideslive.com/38959806/geometric-deep-learning-the-erlangen-programme-of-ml?ref=speaker-16382-latest

Debouch