Decoding DTMF from a WAV file

Question

Following on from my earlier question, my goal is to detect DTMF tones in a WAV file from C#. However, I'm really struggling to understand how this can be done.

I understand the DTMF uses a combination of frequencies, and a Goertzel algorithm can be used ... somehow. I've grabbed a Goertzel code snippet and I've tried shoving a .WAV file into it (using NAudio to read the file, which is a 8KHz mono 16-bit PCM WAV):

 using (WaveFileReader reader = new WaveFileReader(@"dtmftest_w.wav"))
  {
      byte[] buffer = new byte[reader.Length];

      int read = reader.Read(buffer, 0, buffer.Length);
      short[] sampleBuffer = new short[read/2];
      Buffer.BlockCopy(buffer, 0, sampleBuffer, 0, read/2);
      Console.WriteLine(CalculateGoertzel(sampleBuffer,8000,16));                 
   }

 public static double CalculateGoertzel(short[] sample, double frequency, int samplerate)
   {
      double Skn, Skn1, Skn2;
      Skn = Skn1 = Skn2 = 0;
      for (int i = 0; i < sample.Length; i++)
         {
            Skn2 = Skn1;
            Skn1 = Skn;
            Skn = 2 * Math.Cos(2 * Math.PI * frequency / samplerate) * Skn1 - Skn2 + sample[i];
         }
      double WNk = Math.Exp(-2 * Math.PI * frequency / samplerate);
      return 20 * Math.Log10(Math.Abs((Skn - WNk * Skn1)));
    }

I know what I'm doing is wrong: I assume that I should iterate through the buffer, and only calculate the Goertzel value for a small chunk at a time - is this correct?

Secondly, I don't really understand what the output of the Goertzel method is telling me: I get a double (example: 210.985812) returned, but I don't know to equate that to the presence and value of a DTMF tone in the audio file.

I've searched everywhere for an answer, including the libraries referenced in this answer; unfortunately, the code here doesn't appear to work (as noted in the comments on the site). There is a commercial library offered by TAPIEx; I've tried their evaluation library and it does exactly what I need - but they're not responding to emails, which makes me wary about actually purchasing their product.

I'm very conscious that I'm looking for an answer when perhaps I don't know the exact question, but ultimately all I need is a way to find DTMF tones in a .WAV file. Am I on the right lines, and if not, can anyone point me in the right direction?

EDIT: Using @Abbondanza 's code as a basis, and on the (probably fundamentally wrong) assumption that I need to drip-feed small sections of the audio file in, I now have this (very rough, proof-of-concept only) code:

const short sampleSize = 160;

using (WaveFileReader reader = new WaveFileReader(@"\\mac\home\dtmftest.wav"))
        {           
            byte[] buffer = new byte[reader.Length];

            reader.Read(buffer, 0, buffer.Length);

            int bufferPos = 0;

            while (bufferPos < buffer.Length-(sampleSize*2))
            {
                short[] sampleBuffer = new short[sampleSize];
                Buffer.BlockCopy(buffer, bufferPos, sampleBuffer, 0, sampleSize*2);


                var frequencies = new[] {697.0, 770.0, 852.0, 941.0, 1209.0, 1336.0, 1477.0};

                var powers = frequencies.Select(f => new
                {
                    Frequency = f,
                   Power = CalculateGoertzel(sampleBuffer, f, 8000)              
                });

                const double AdjustmentFactor = 1.05;
                var adjustedMeanPower = AdjustmentFactor*powers.Average(result => result.Power);

                var sortedPowers = powers.OrderByDescending(result => result.Power);
                var highestPowers = sortedPowers.Take(2).ToList();

                float seconds = bufferPos / (float)16000;

                if (highestPowers.All(result => result.Power > adjustedMeanPower))
                {
                    // Use highestPowers[0].Frequency and highestPowers[1].Frequency to 
                    // classify the detected DTMF tone.

                    switch (Convert.ToInt32(highestPowers[0].Frequency))
                    {
                        case 1209:
                            switch (Convert.ToInt32(highestPowers[1].Frequency))
                            {
                                case 697:
                                    Console.WriteLine("1 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 770:
                                    Console.WriteLine("4 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 852:
                                    Console.WriteLine("7 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 941:
                                    Console.WriteLine("* pressed at " + bufferPos);
                                    break;
                            }
                            break;
                        case 1336:
                            switch (Convert.ToInt32(highestPowers[1].Frequency))
                            {
                                case 697:
                                    Console.WriteLine("2 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 770:
                                    Console.WriteLine("5 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 852:
                                    Console.WriteLine("8 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 941:
                                    Console.WriteLine("0 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                            }
                            break;
                        case 1477:
                            switch (Convert.ToInt32(highestPowers[1].Frequency))
                            {
                                case 697:
                                    Console.WriteLine("3 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 770:
                                    Console.WriteLine("6 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 852:
                                    Console.WriteLine("9 pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                                case 941:
                                    Console.WriteLine("# pressed at " + bufferPos + " (" + seconds + "s)");
                                    break;
                            }
                            break;
                    }
                }
                else
                {
                    Console.WriteLine("No DTMF at " + bufferPos + " (" + seconds + "s)");
                }
                bufferPos = bufferPos + (sampleSize*2);
            }

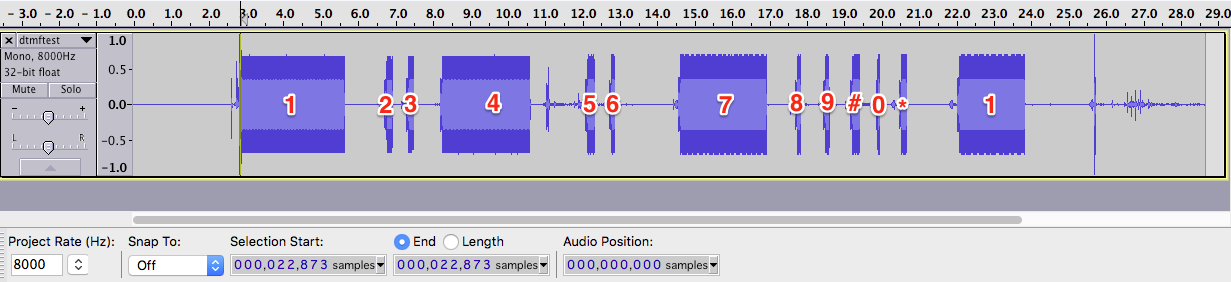
This is the sample file as viewed in Audacity; I've added in the DTMF keypresses that were pressed-

and ... it almost works. From the file above, I shouldn't see any DTMF until almost exactly 3 seconds in, however, my code reports:

9 pressed at 1920 (0.12s)
1 pressed at 2880 (0.18s)
* pressed at 3200
1 pressed at 5120 (0.32s)
1 pressed at 5440 (0.34s)
7 pressed at 5760 (0.36s)
7 pressed at 6080 (0.38s)
7 pressed at 6720 (0.42s)
5 pressed at 7040 (0.44s)
7 pressed at 7360 (0.46s)
7 pressed at 7680 (0.48s)
1 pressed at 8000 (0.5s)
7 pressed at 8320 (0.52s)

... until it gets to 3 seconds, and THEN it starts to settle down to the correct answer: that 1 was pressed:

7 pressed at 40000 (2.5s)
# pressed at 43840 (2.74s)
No DTMF at 44800 (2.8s)
1 pressed at 45120 (2.82s)
1 pressed at 45440 (2.84s)
1 pressed at 46080 (2.88s)
1 pressed at 46720 (2.92s)
4 pressed at 47040 (2.94s)
1 pressed at 47360 (2.96s)
1 pressed at 47680 (2.98s)
1 pressed at 48000 (3s)
1 pressed at 48960 (3.06s)
4 pressed at 49600 (3.1s)
1 pressed at 49920 (3.12s)
1 pressed at 50560 (3.16s)
1 pressed at 51520 (3.22s)
1 pressed at 52160 (3.26s)
4 pressed at 52480 (3.28s)

If I bump up the AdjustmentFactor beyond 1.2, I get very little detection at all.

I sense that I'm almost there, but can anyone see what it is I'm missing?

EDIT2: The test file above is available here. The adjustedMeanPower in the example above is 47.6660450354638, and the powers are:

Ferrand

The DTMF tome should be at least 40ms long with a space at least 40ms. See genave.com/dtmf-mark-space.htm – Insulation

Also the frequencies you need to detect are 697Hz, 770Hz, 852Hz, 941Hz, 1209Hz, 1336Hz and 1477Hz as per genave.com/dtmf.htm – Insulation

I added a code snippet to my answer. Let me know if it helped you to make progress on your problem. – Grissom

@SteveFord: so does this mean that I should be moving through the file in 40ms segments? – Ferrand

@Abbondanza: it has, thank you - see above, hopefully I'm close to solving this! – Ferrand

Looks like you're getting there! Can you add the content of powers and the value of adjustedMeanPower to your debug output? Also, out of curiosity, I'd like to fiddle around with that problem a bit. Is there a way you can make your test WAV file accessible to me? – Grissom

@Abbondanza: Added above, thanks! – Ferrand

@KenD, please see my updated answer. – Grissom

@KenD, where do you got that Goertzel implementation from? It gives to high powers for frequencies that are actually not present in a sample. – Grissom

I'm afraid I snagged it from this question: #28367002. The good news is that your new code appears to work perfectly, I'm just testing it on another few files but so far so good! Is there a better implementation of Goertzel I should be using? – Ferrand

@KenD, I think the implementation is fine. We just used it incorrectly. See the 2nd update in my answer. – Grissom

@KenD, I re-wrote the prototype. It gives much, much more pronounced magnitude differences between missing and present frequencies. Also it's faster (but still not fully optimized). I highly recommend you take a look at the third (and final ;) update in my answer. Full code: pastebin.com/serxw5nG – Grissom

Answer 1

CalculateGoertzel() returns the power of the selected frequency within the provided sample.

Calculate this power for each of the DTMF frequencies (697, 770, 852, 941, 1209, 1336, and 1477 Hz), sort the resulting powers and pick the highest two. If both are above a certain threshold then a DTMF tone has been detected.

What you use as threshold depends on the signal to noise ratio (SNR) of your sample. For a start it should be sufficient to calculate the mean of all Goerzel values, multiply the mean by a factor (e.g. 2 or 3), and check if the two highest Goerzel values are above that value.

Here is a code snippet to express what I mean in a more formal way:

var frequencies = new[] {697.0, 770.0, 852.0, 941.0, 1209.0, 1336.0, 1477.0};

var powers = frequencies.Select(f => new
{
    Frequency = f,
    Power = CalculateGoerzel(sample, f, samplerate)
});

const double AdjustmentFactor = 1.0;
var adjustedMeanPower = AdjustmentFactor * powers.Average(result => result.Power);

var sortedPowers = powers.OrderByDescending(result => result.Power);
var highestPowers = sortedPowers.Take(2).ToList();

if (highestPowers.All(result => result.Power > adjustedMeanPower))
{
    // Use highestPowers[0].Frequency and highestPowers[1].Frequency to 
    // classify the detected DTMF tone.
}

Start with an AdjustmentFactor of 1.0. If you get false positives from your test data (i.e. you detect DTMF tones in samples where there shouldn't be any DTMF tones), keep increasing it until the false positives stop.

---

Update #1

I tried your code on the wave file and adjusted a few things:

I materialized the enumerable after the Goertzel calculation (important for performance):

var powers = frequencies.Select(f => new
{
    Frequency = f,
    Power = CalculateGoertzel(sampleBuffer, f, 8000)
// Materialize enumerable to avoid multiple calculations.
}).ToList();

I didn't use the adjusted mean for thresholding. I just used 100.0 as threshold:

if (highestPowers.All(result => result.Power > 100.0))
{
     ...
}

I doubled the sample size (I believe you used 160):

int sampleSize = 160 * 2;

I fixed your DTMF classification. I used nested dictionaries to capture all possible cases:

var phoneKeyOf = new Dictionary<int, Dictionary<int, string>>
{
    {1209, new Dictionary<int, string> {{1477, "?"}, {1336, "?"}, {1209, "?"}, {941, "*"}, {852, "7"}, {770, "4"}, {697, "1"}}},
    {1336, new Dictionary<int, string> {{1477, "?"}, {1336, "?"}, {1209, "?"}, {941, "0"}, {852, "8"}, {770, "5"}, {697, "2"}}},
    {1477, new Dictionary<int, string> {{1477, "?"}, {1336, "?"}, {1209, "?"}, {941, "#"}, {852, "9"}, {770, "6"}, {697, "3"}}},
    { 941, new Dictionary<int, string> {{1477, "#"}, {1336, "0"}, {1209, "*"}, {941, "?"}, {852, "?"}, {770, "?"}, {697, "?"}}},
    { 852, new Dictionary<int, string> {{1477, "9"}, {1336, "8"}, {1209, "7"}, {941, "?"}, {852, "?"}, {770, "?"}, {697, "?"}}},
    { 770, new Dictionary<int, string> {{1477, "6"}, {1336, "5"}, {1209, "4"}, {941, "?"}, {852, "?"}, {770, "?"}, {697, "?"}}},
    { 697, new Dictionary<int, string> {{1477, "3"}, {1336, "2"}, {1209, "1"}, {941, "?"}, {852, "?"}, {770, "?"}, {697, "?"}}}
}

The phone key is then retrieved with:

var key = phoneKeyOf[(int)highestPowers[0].Frequency][(int)highestPowers[1].Frequency];

The results are not perfect, but somewhat reliable.

---

Update #2

I think I figured out the problem, but can't try it out myself right now. You cannot pass the target frequenzy directly to CalculateGoertzel(). It has to be normalized to be centered over the DFT bins. When calculating the powers try this approach:

var powers = frequencies.Select(f => new
{
    Frequency = f,
    // Pass normalized frequenzy
    Power = CalculateGoertzel(sampleBuffer, Math.Round(f*sampleSize/8000.0), 8000)
}).ToList();

Also you have to use 205 as sampleSize in order the minimize the error.

---

Update #3

I re-wrote the prototype to use NAudio's ISampleProvider interface, which returns normalized sample values (floats in range [-1.0; 1.0]). Also I re-wrote CalculateGoertzel() from scratch. It's still not performance optimized, but gives much, much more pronounced power differences between frequencies. There are no more false positives when I run it your test data. I highly recommend you take a look at it: http://pastebin.com/serxw5nG

---

Update #4

I created a GitHub project and two NuGet packages to detect DTMF tones in live (captured) audio and pre-recorded audio files.

Grissom

Update #2 didn't work for me, I'm afraid; I didn't get any results from the test file. However, the code in update #1 works (almost) perfectly, certainly good enough for my purposes. Thank you very much for your help, I wouldn't have figured it out without you! – Ferrand

@moose, how so? Do you mind creating an issue on the projects' github site? – Grissom

@GNNP, btw, in what version of Visual Studio can you build the solution without any modifications? VS2013 reports 163 errors. – Sb

@moose, too bad you don't have the time file a simple bug report or at least explain yourself a bit. I'll have to see when I find the time to bother. – Grissom

@moose, I verified your problem and created an issue on the github site. If you have any ideas: comments and pull requests are much appreciated. – Grissom

Hi, I'm translating this into Python. I am wondering why this assignment does not seem to be used in the first code snippet. Frequency = f, – Reld

@developer01, it's needed for the last step (classification) which hasn't been implemented. – Grissom

@GoodNightNerdPride Hey how would you handle the case in which you don't know how long a DTMF tone is? Or could you point me to some resources? – Reld

@developer01, the C# library in my post can handle those. Check out the detector implementation on GitHub to see how it does that. – Grissom