Update in Segment Tree

Question

I am learning segment tree , i came across this question. There are Array A and 2 type of operation

1. Find the Sum in Range L to R 
2. Update the Element in Range L to R by Value X.

Update should be like this

A[L] = 1*X;
A[L+1] = 2*X;
A[L+2] = 3*X;
A[R] = (R-L+1)*X;

How should i handle the second type of query can anyone please give some algorithm to modify by segment tree , or there is a better solution

Reilly

Is there any limit of update query in your problem? I mean how much update query likely to be given? – Fez

@KaidulIslam Q is in Range Between 0 to 10^5 – Reilly

It seems lazy propagation can be possible but with some extra complication and space. Besides updating each array index sequentially is also possible but will be very inefficient. – Fez

Answer 1

So, it is needed to update efficiently the interval [L,R] with to the corresponding values of the arithmetic progression with the step X, and to be able to find efficiently the sums over the different intervals.

In order to solve this problem efficiently - let's make use of the Segment Tree with Lazy Propagation.

The basic ideas are following:

• The arithmetic progression can be defined by the first and last items and the amount of items

• It is possible to obtain a new arithmetic progression by combination of the first and last items of two different arithmetic progressions (which have the same amount of items). The first and last items of the new arithmetic progression will be just a combination of the corresponding items of combined arithmetic progressions

• Hence, we can associate with each node of the Segment Tree - the first and last values of the arithmetic progression, which spans over the given interval

• During update, for all affected intervals, we can lazily propagate through the Segment Tree - the values of the first and last items, and update the aggregated sums on these intervals.

So, the node of the Segment Tree for given problem will have structure:

class Node {
    int left; // Left boundary of the current SegmentTree node
    int right; // Right boundary of the current SegmentTree node

    int sum; // Sum on the interval [left,right]

    int first; // First item of arithmetic progression inside given node
    int last; // Last item of arithmetic progression

    Node left_child;
    Node right_child;

    // Constructor
    Node(int[] arr, int l, int r) { ... }

    // Add arithmetic progression with step X on the interval [l,r]
    // O(log(N))
    void add(int l, int r, int X) { ... }

    // Request the sum on the interval [l,r]
    // O(log(N))
    int query(int l, int r) { ... }

    // Lazy Propagation
    // O(1)
    void propagate() { ... }
}

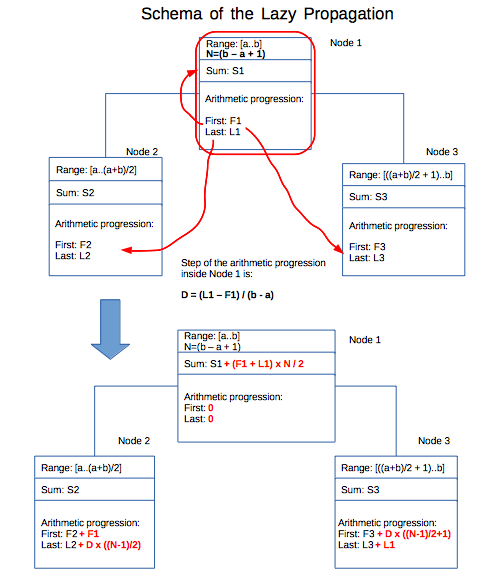
The specificity of the Segment Tree with Lazy Propagation is such, that every time, when the node of the tree is traversed - the Lazy Propagation routine (which has complexity O(1)) is executed for the given node. So, below is provided the illustration of the Lazy Propagation logic for some arbitrary node, which has children:

As you can see, during the Lazy Propagation the first and the last items of the arithmetic progressions of the child nodes are updated, also the sum inside the parent node is updated as well.

Implementation

Below provided the Java implementation of the described approach (with additional comments):

class Node {
    int left; // Left boundary of the current SegmentTree node
    int right; // Right boundary of the current SegmentTree node
    int sum; // Sum on the interval
    int first; // First item of arithmetic progression
    int last; // Last item of arithmetic progression
    Node left_child;
    Node right_child;

    /**
     * Construction of a Segment Tree
     * which spans over the interval [l,r]
     */
    Node(int[] arr, int l, int r) {
        left = l;
        right = r;
        if (l == r) { // Leaf
            sum = arr[l];
        } else { // Construct children
            int m = (l + r) / 2;
            left_child = new Node(arr, l, m);
            right_child = new Node(arr, m + 1, r);
            // Update accumulated sum
            sum = left_child.sum + right_child.sum;
        }
    }

    /**
     * Lazily adds the values of the arithmetic progression
     * with step X on the interval [l, r]
     * O(log(N))
     */
    void add(int l, int r, int X) {
        // Lazy propagation
        propagate();
        if ((r < left) || (right < l)) {
            // If updated interval doesn't overlap with current subtree
            return;
        } else if ((l <= left) && (right <= r)) {
            // If updated interval fully covers the current subtree
            // Update the first and last items of the arithmetic progression
            int first_item_offset = (left - l) + 1;
            int last_item_offset = (right - l) + 1;
            first = X * first_item_offset;
            last = X * last_item_offset;
            // Lazy propagation
            propagate();
        } else {
            // If updated interval partially overlaps with current subtree
            left_child.add(l, r, X);
            right_child.add(l, r, X);
            // Update accumulated sum
            sum = left_child.sum + right_child.sum;
        }
    }

    /**
     * Returns the sum on the interval [l, r]
     * O(log(N))
     */
    int query(int l, int r) {
        // Lazy propagation
        propagate();
        if ((r < left) || (right < l)) {
            // If requested interval doesn't overlap with current subtree
            return 0;
        } else if ((l <= left) && (right <= r)) {
            // If requested interval fully covers the current subtree
            return sum;
        } else {
            // If requested interval partially overlaps with current subtree
            return left_child.query(l, r) + right_child.query(l, r);
        }
    }

    /**
     * Lazy propagation
     * O(1)
     */
    void propagate() {
        // Update the accumulated value
        // with the sum of Arithmetic Progression
        int items_count = (right - left) + 1;
        sum += ((first + last) * items_count) / 2;
        if (right != left) { // Current node is not a leaf
            // Calculate the step of the Arithmetic Progression of the current node
            int step = (last - first) / (items_count - 1);
            // Update the first and last items of the arithmetic progression
            // inside the left and right subtrees
            // Distribute the arithmetic progression between child nodes
            // [a(1) to a(N)] -> [a(1) to a(N/2)] and [a(N/2+1) to a(N)]
            int mid = (items_count - 1) / 2;
            left_child.first += first;
            left_child.last += first + (step * mid);
            right_child.first += first + (step * (mid + 1));
            right_child.last += last;
        }
        // Reset the arithmetic progression of the current node
        first = 0;
        last = 0;
    }
}

The Segment Tree in provided solution is implemented explicitly - using objects and references, however it can be easily modified in order to make use of the arrays instead.

Testing

Below provided the randomized tests, which compare two implementations:

• Processing queries by sequential increase of each item of the array with O(N) and calculating the sums on intervals with O(N)
• Processing the same queries using Segment Tree with O(log(N)) complexity:

The Java implementation of the randomized tests:

public static void main(String[] args) {
    // Initialize the random generator with predefined seed,
    // in order to make the test reproducible
    Random rnd = new Random(1);

    int test_cases_num = 20;
    int max_arr_size = 100;
    int num_queries = 50;
    int max_progression_step = 20;

    for (int test = 0; test < test_cases_num; test++) {
        // Create array of the random length
        int[] arr = new int[rnd.nextInt(max_arr_size) + 1];
        Node segmentTree = new Node(arr, 0, arr.length - 1);

        for (int query = 0; query < num_queries; query++) {
            if (rnd.nextDouble() < 0.5) {
                // Update on interval [l,r]
                int l = rnd.nextInt(arr.length);
                int r = rnd.nextInt(arr.length - l) + l;
                int X = rnd.nextInt(max_progression_step);
                update_sequential(arr, l, r, X); // O(N)
                segmentTree.add(l, r, X); // O(log(N))
            }
            else {
                // Request sum on interval [l,r]
                int l = rnd.nextInt(arr.length);
                int r = rnd.nextInt(arr.length - l) + l;
                int expected = query_sequential(arr, l, r); // O(N)
                int actual = segmentTree.query(l, r); // O(log(N))
                if (expected != actual) {
                    throw new RuntimeException("Results are different!");
                }
            }
        }
    }
    System.out.println("All results are equal!");
}

static void update_sequential(int[] arr, int left, int right, int X) {
    for (int i = left; i <= right; i++) {
        arr[i] += X * ((i - left) + 1);
    }
}

static int query_sequential(int[] arr, int left, int right) {
    int sum = 0;
    for (int i = left; i <= right; i++) {
        sum += arr[i];
    }
    return sum;
}

Lanai

What if change it to Find the Sum in Range L to R to Find the Multiple in Range L to R – Reilly

Answer 2

Basically you need to make a tree and then make updates using lazy propagation, here is the implementation.

int tree[1 << 20], Base = 1 << 19;
int lazy[1 << 20];
void propagation(int v){ //standard propagation
  tree[v * 2] += lazy[v];
  tree[v * 2 + 1] += lazy[v];
  lazy[v * 2] += lazy[v];
  lazy[v * 2 + 1] += lazy[v];
  lazy[v] == 0;
}
void update(int a, int b, int c, int v = 1, int p = 1, int k = Base){
  if(p > b || k < a) return; //if outside range [a, b]
  propagation(v);
  if(p >= a && k <= b){ // if fully inside range [a, b]
    tree[v] += c;
    lazy[v] += c;
    return;
  }
  update(a, b, c, v * 2, p, (p + k) / 2); //left child
  update(a, b, c, v * 2 + 1, (p + k) / 2 + 1, k); //right child
  tree[v] = tree[v * 2] + tree[v * 2 + 1]; //update current node
}
int query(int a, int b, int v = 1, int p = 1, int k = Base){
  if(p > b || k < a) //if outside range [a, b]
    return 0;
  propagation(v);
  if(p >= a && k <= b) // if fully inside range [a, b]
    return tree[v];
  int res = 0;
  res += query(a, b, c, v * 2, p, (p + k) / 2); //left child
  res += query(a, b, c, v * 2 + 1, (p + k) / 2 + 1, k); //right child
  tree[v] = tree[v * 2] + tree[v * 2 + 1]; //update current node
  return res;
}

update function oviously updates the tree so it adds to nodes on interval [a, b] (or [L, R])

update(L, R, value);

query function just gives you sum of elements in range

query(L, R);

Ballenger

Answer 3

The second operation can be regarded as adding a segment to the interval [L,R] with two endpoints (L,x),(R,(R-L+1)*x) and slope 1.

The most important thing to consider about segment tree with interval modifications is whether the lazy tags can be merged. If we regard the modification as adding segments, we can find that two segments can be easily merged - we only need to update the slope and the endpoints. For each interval, we only need to maintain the slope and the starting point of the segment for this interval. By using lazy tag technique, we can easily implement querying interval sums and doing interval modifications in O(nlogn) time complexity.

Nympho