What is the difference between contiguous and non-contiguous arrays?

Question

In the numpy manual about the reshape() function, it says

>>> a = np.zeros((10, 2))
# A transpose make the array non-contiguous
>>> b = a.T
# Taking a view makes it possible to modify the shape without modifying the
# initial object.
>>> c = b.view()
>>> c.shape = (20)
AttributeError: incompatible shape for a non-contiguous array

My questions are:

1. What are continuous and noncontiguous arrays? Is it similar to the contiguous memory block in C like What is a contiguous memory block?
2. Is there any performance difference between these two? When should we use one or the other?
3. Why does transpose make the array non-contiguous?
4. Why does c.shape = (20) throws an error incompatible shape for a non-contiguous array?

Thanks for your answer!

Halimeda

Answer 1

A contiguous array is just an array stored in an unbroken block of memory: to access the next value in the array, we just move to the next memory address.

Consider the 2D array arr = np.arange(12).reshape(3,4). It looks like this:

In the computer's memory, the values of arr are stored like this:

This means arr is a C contiguous array because the rows are stored as contiguous blocks of memory. The next memory address holds the next row value on that row. If we want to move down a column, we just need to jump over three blocks (e.g. to jump from 0 to 4 means we skip over 1,2 and 3).

Transposing the array with arr.T means that C contiguity is lost because adjacent row entries are no longer in adjacent memory addresses. However, arr.T is Fortran contiguous since the columns are in contiguous blocks of memory:

---

Performance-wise, accessing memory addresses which are next to each other is very often faster than accessing addresses which are more "spread out" (fetching a value from RAM could entail a number of neighbouring addresses being fetched and cached for the CPU.) This means that operations over contiguous arrays will often be quicker.

As a consequence of C contiguous memory layout, row-wise operations are usually faster than column-wise operations. For example, you'll typically find that

np.sum(arr, axis=1) # sum the rows

is slightly faster than:

np.sum(arr, axis=0) # sum the columns

Similarly, operations on columns will be slightly faster for Fortran contiguous arrays.

---

Finally, why can't we flatten the Fortran contiguous array by assigning a new shape?

>>> arr2 = arr.T
>>> arr2.shape = 12
AttributeError: incompatible shape for a non-contiguous array

In order for this to be possible NumPy would have to put the rows of arr.T together like this:

(Setting the shape attribute directly assumes C order - i.e. NumPy tries to perform the operation row-wise.)

This is impossible to do. For any axis, NumPy needs to have a constant stride length (the number of bytes to move) to get to the next element of the array. Flattening arr.T in this way would require skipping forwards and backwards in memory to retrieve consecutive values of the array.

If we wrote arr2.reshape(12) instead, NumPy would copy the values of arr2 into a new block of memory (since it can't return a view on to the original data for this shape).

Above

I am having difficulty understanding this, can you please elaborate a little? In the latest graphical representation of the impossible ordering in the memory actually the strides are constant in my opinion. For example to go from 0 to 1 the stride is 1 byte (let's say each element is a byte) and it is the same for each column. Likewise the stride is 4 bytes for to go from one element in the row to the next one and it is also constant. – Duffer

@Duffer the failed reshape of the 2D arr2 to the 1D shape (12,) uses C order, meaning that that axis 1 is unwound before axis 0 (i.e. each of the four rows needs to be placed next to each other to create desired the 1D array). It is impossible to read this sequence of integers (0, 4, 8, 1, 5, 9, 2, 6, 10, 3, 7, 11) out of the buffer using a constant stride length (the bytes to jump to visit these elements in sequence would be 4, 4, -7, 4, 4, -7, 4, 4, 7, 4, 4). NumPy requires a contant stride length per axis. – Above

Thanks at first I thought it will create a new array, but it uses the memory of the old one. – Duffer

@AlexRiley What happens behind the scenes when an array is marked neighter C or F ordered? For instance, take every NxD array arr, and print(arr[:,::-1].flags). What happens in this situation? I guess the array is indeed C or F ordered, but which one of those? And which optimizations of numpy we lose if both flags are False? – Punctuation

@Jjang: whether NumPy considers the array is C or F order is dependent entirely on shape and strides (the criteria are here). So while arr[:, ::-1] is a view of the same memory buffer as arr, NumPy does not consider it C or F order as it has traverse the values in the buffer in a "non-standard" order... – Above

... Regarding optimisations, one thing to mention is that NumPy considers C or F contiguous arrays to be "trivially iterable" and will bypass setting up a more expensive general multi-dimsensional iterator object to traverse such arrays in some cases. – Above

@AlexRiley So basically you say it will scan all the array everytime to reach an index (i.e. no strides)? I showed a performance gain by replacing a np.copy() function which copies and converts to C-order, to a view which is neither C ot F ordered. Want to elaborate more here? – Punctuation

@Jjang: not sure I understand what you mean by "scan all the array everytime to reach an index" - the contiguous flags are set on the array's creation by inspecting the array's shape and strides (not the values in the array). In any case I'll make some time to have a look at the question you've linked to. – Above

Answer 2

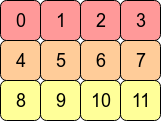
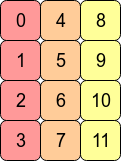
Maybe this example with 12 different array values will help:

In [207]: x=np.arange(12).reshape(3,4).copy()

In [208]: x.flags
Out[208]: 
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  ...
In [209]: x.T.flags
Out[209]: 
  C_CONTIGUOUS : False
  F_CONTIGUOUS : True
  OWNDATA : False
  ...

The C order values are in the order that they were generated in. The transposed ones are not

In [212]: x.reshape(12,)   # same as x.ravel()
Out[212]: array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

In [213]: x.T.reshape(12,)
Out[213]: array([ 0,  4,  8,  1,  5,  9,  2,  6, 10,  3,  7, 11])

You can get 1d views of both

In [214]: x1=x.T

In [217]: x.shape=(12,)

the shape of x can also be changed.

In [220]: x1.shape=(12,)
---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-220-cf2b1a308253> in <module>()
----> 1 x1.shape=(12,)

AttributeError: incompatible shape for a non-contiguous array

But the shape of the transpose cannot be changed. The data is still in the 0,1,2,3,4... order, which can't be accessed accessed as 0,4,8... in a 1d array.

But a copy of x1 can be changed:

In [227]: x2=x1.copy()

In [228]: x2.flags
Out[228]: 
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  ...
In [229]: x2.shape=(12,)

Looking at strides might also help. A strides is how far (in bytes) it has to step to get to the next value. For a 2d array, there will be be 2 stride values:

In [233]: x=np.arange(12).reshape(3,4).copy()

In [234]: x.strides
Out[234]: (16, 4)

To get to the next row, step 16 bytes, next column only 4.

In [235]: x1.strides
Out[235]: (4, 16)

Transpose just switches the order of the strides. The next row is only 4 bytes- i.e. the next number.

In [236]: x.shape=(12,)

In [237]: x.strides
Out[237]: (4,)

Changing the shape also changes the strides - just step through the buffer 4 bytes at a time.

In [238]: x2=x1.copy()

In [239]: x2.strides
Out[239]: (12, 4)

Even though x2 looks just like x1, it has its own data buffer, with the values in a different order. The next column is now 4 bytes over, while the next row is 12 (3*4).

In [240]: x2.shape=(12,)

In [241]: x2.strides
Out[241]: (4,)

And as with x, changing the shape to 1d reduces the strides to (4,).

For x1, with data in the 0,1,2,... order, there isn't a 1d stride that would give 0,4,8....

__array_interface__ is another useful way of displaying array information:

In [242]: x1.__array_interface__
Out[242]: 
{'strides': (4, 16),
 'typestr': '<i4',
 'shape': (4, 3),
 'version': 3,
 'data': (163336056, False),
 'descr': [('', '<i4')]}

The x1 data buffer address will be same as for x, with which it shares the data. x2 has a different buffer address.

You could also experiment with adding a order='F' parameter to the copy and reshape commands.

Feininger