Which is the fastest algorithm to find out prime numbers using C++? I have used sieve's algorithm but I still want it to be faster!
Which is the fastest algorithm to find prime numbers?
A very fast implementation of the Sieve of Atkin is Dan Bernstein's primegen. This sieve is more efficient than the Sieve of Eratosthenes. His page has some benchmark information.
Actually I don't think primegen is the fastest, or even the second-fastest; yafu and primesieve are both faster in general, I think, and certainly over 2^32. Both are (modified) sieves of Eratosthenes rather than the Atkin-Bernstein sieve. –
Windbag
Primesieve Sieve of Eratosthenes (SoE) is the very fastest algorithm possible and will always be faster than any implementation of the Sieve of Atkin SoA, including Bernstein's as linked in this answer because primesieve reduces the number of operations compared to SoA: For the 32-bit number range (2^32 - 1), primesieve does about 1.2 billion culls whereas SoA does a total of about 1.4 billion combined toggle and square free operations, both operations being of about the same complexity and able to be optimized in about the same way. –
Bourg
Continued: Bernstein only compared the SoE using the same effective wheel factorization as for the SoA, which is a 2;3;5 wheel, use of which wheel results in about 1.83 billion culls over the 32-bit number range; this makes the SoA about 30% faster when comparing this restricted version of SoE for equivalent other optimizations. However, the primesieve algorithm uses a 2;3;5;7 wheel in combination with a 2;3;5;7;11;13;17 wheel segment pre-cull to reduce the number of operations to about 1.2 billion to run about 16.7% faster than SoA with equivalent operation loop optimizations. –
Bourg
Continued2: The SoA con not have higher factor wheel factorization used to make much of a difference as the 2;3;5 factorization wheel is a "baked-in" part of the algorithm. –
Bourg
@Bourg if wikipedia is to believed, the atkin's sieve has a (very) slightly better computational complexity by a factor
log log N Of course, this is so tiny it isn't going to matter much more than generic tuning. –
Clue @Eamon Nerbonne, WP is correct; however, just having a slightly better computational complexity doesn't make a faster algorithms for general use. In these comments, I am referring to that maximum wheel factorization of the Sieve of Eratosthenes (SoE) (which is not possible for the Sieve of Atkin- SoA) makes for slightly less operations for the SoE up to a range of about a billion. Much above that point, one generally needs to use page segmentation to overcome memory limitations, and that is where the SoA fails, taking rapidly increasing amounts of constant overhead with increasing range. –
Bourg
Q. Does anyone have any clue how to use the Sieve of Atkin by calling a native in Java? in other words, I would like to bridge the library written in C from Java using native rather than re-writing it in Java? –
Baseball
If it has to be really fast you can include a list of primes:
http://www.bigprimes.net/archive/prime/
If you just have to know if a certain number is a prime number, there are various prime tests listed on wikipedia. They are probably the fastest method to determine if large numbers are primes, especially because they can tell you if a number is not a prime.
A list of all primes? I think you mean a list of the first few primes... :) –
Subteen
If you call 100000000 a few, then yes. :) –
Disarmament
surely 100000000 is "a few" comparing to infinity ;) –
Theomania
Why do you think that the Sieve of Atkin (SoA) is faster than the Sieve of Eratosthenes (SoE)? It certainly isn't when one just implements a program using the pseudo code as in the Wikipedia article you linked. If the SoE is implemented with a similar level of possible optimizations as are used with the SoA, then there are slightly less operations for very large sieving ranges for SoA than for SoE, but that gain is usually more than offset by the increased complexity and the extra constant factor overhead of this computational complexity such that for practical applications the SoE is better. –
Bourg
That's the nice thing about prime numbers, they don't change. Once you have a list you can keep reusing it forever. –
Counterpoison
@MarkRansom the question as posted is, how to get that list. "take it from someone else who already did it before" is not an answer. –
Cothran
@WillNess the question specifically asks for the "fastest", and surely nothing will be faster than reading a list that already exists. There's nothing to prevent you from building your own list the slow way if it bothers you to use someone else's. –
Counterpoison
@MarkRansom so the answer must show the slow way first. it's not what bothers me or not, the question asks how to do it -- someone has to be the first. it can't be copied from someone else ad infinitum -- there must be a base case. –
Cothran
@WillNess the question already admits to having a sieve solution, with their only complaint being the slowness of it. –
Counterpoison
@MarkRansom so they want it faster and you propose them to use the slow one first? it still doesn't work for me. :) and BTW I've seen it stated on SO that running a good SoE is faster than reading a list from a file. :) –
Cothran
@WillNess I would welcome seeing the evidence that SoE is faster than reading from a file. I'm sure a lot depends on the file format. –
Counterpoison
@MarkRansom Sorry, just saw it somewhere here in the comments. :) IIRC. –
Cothran
Until now, I believe that the fastest prime number testing algorithm is Strong Probable Prime (SPRP). I am quoting from Nvidia CUDA forums:
One of the more practical niche problems in number theory has to do with identification of prime numbers. Given N, how can you efficiently determine if it is prime or not? This is not just a thoeretical problem, it may be a real one needed in code, perhaps when you need to dynamically find a prime hash table size within certain ranges. If N is something on the order of 2^30, do you really want to do 30000 division tests to search for any factors? Obviously not.
The common practical solution to this problem is a simple test called an Euler probable prime test, and a more powerful generalization called a Strong Probable Prime (SPRP). This is a test that for an integer N can probabilistically classify it as prime or not, and repeated tests can increase the correctness probability. The slow part of the test itself mostly involves computing a value similar to A^(N-1) modulo N. Anyone implementing RSA public-key encryption variants has used this algorithm. It's useful both for huge integers (like 512 bits) as well as normal 32 or 64 bit ints.
The test can be changed from a probabilistic rejection into a definitive proof of primality by precomputing certain test input parameters which are known to always succeed for ranges of N. Unfortunately the discovery of these "best known tests" is effectively a search of a huge (in fact infinite) domain. In 1980, a first list of useful tests was created by Carl Pomerance (famous for being the one to factor RSA-129 with his Quadratic Seive algorithm.) Later Jaeschke improved the results significantly in 1993. In 2004, Zhang and Tang improved the theory and limits of the search domain. Greathouse and Livingstone have released the most modern results until now on the web, at http://math.crg4.com/primes.html, the best results of a huge search domain.
See here for more info: http://primes.utm.edu/prove/prove2_3.html and http://forums.nvidia.com/index.php?showtopic=70483
If you just need a way to generate very big prime numbers and don't care to generate all prime numbers < an integer n, you can use Lucas-Lehmer test to verify Mersenne prime numbers. A Mersenne prime number is in the form of 2^p -1. I think that Lucas-Lehmer test is the fastest algorithm discovered for Mersenne prime numbers.
And if you not only want to use the fastest algorithm but also the fastest hardware, try to implement it using Nvidia CUDA, write a kernel for CUDA and run it on GPU.
You can even earn some money if you discover large enough prime numbers, EFF is giving prizes from $50K to $250K: https://www.eff.org/awards/coop
There is a 100% mathematical test that will check if a number P is prime or composite, called AKS Primality Test.
The concept is simple: given a number P, if all the coefficients of (x-1)^P - (x^P-1) are divisible by P, then P is a prime number, otherwise it is a composite number.
For instance, given P = 3, would give the polynomial:
(x-1)^3 - (x^3 - 1)
= x^3 + 3x^2 - 3x - 1 - (x^3 - 1)
= 3x^2 - 3x
And the coefficients are both divisible by 3, therefore the number is prime.
And example where P = 4, which is NOT a prime would yield:
(x-1)^4 - (x^4-1)
= x^4 - 4x^3 + 6x^2 - 4x + 1 - (x^4 - 1)
= -4x^3 + 6x^2 - 4x
And here we can see that the coefficients 6 is not divisible by 4, therefore it is NOT prime.
The polynomial (x-1)^P will P+1 terms and can be found using combination. So, this test will run in O(n) runtime, so I don't know how useful this would be since you can simply iterate over i from 0 to p and test for the remainder.
AKS is a very slow method in practice, not competitive with other known methods. The method you describe is not AKS but an opening lemma that is slower than unoptimized trial division (as you point out). –
Luff
hello @Kousha, what does the
x stands for? in (x-1)^P - (x^P-1). do you have a sample code for this? in C++ for determining if the integer is prime or not? –
Sashenka @Sashenka X is just a variable. It's the coefficient of X that determine whether or not the number is prime or not. And no I do not have the code. I don't recommend to actually use this method for determining if a number is prime or not. This is just a very cool mathematical behaviour of prime numbers, but otherwise it's incredibly inefficient. –
Resolvent
Is your problem to decide whether a particular number is prime? Then you need a primality test (easy). Or do you need all primes up to a given number? In that case prime sieves are good (easy, but require memory). Or do you need the prime factors of a number? This would require factorization (difficult for large numbers if you really want the most efficient methods). How large are the numbers you are looking at? 16 bits? 32 bits? bigger?
One clever and efficient way is to pre-compute tables of primes and keep them in a file using a bit-level encoding. The file is considered one long bit vector whereas bit n represents integer n. If n is prime, its bit is set to one and to zero otherwise. Lookup is very fast (you compute the byte offset and a bit mask) and does not require loading the file in memory.
A good primality test is competitive with main memory latency for prime tables that could reasonably fit, so I wouldn't use this unless it could fit into L2. –
Windbag
Rabin-Miller is a standard probabilistic primality test. (you run it K times and the input number is either definitely composite, or it is probably prime with probability of error 4-K. (a few hundred iterations and it's almost certainly telling you the truth)
There is a non-probabilistic (deterministic) variant of Rabin Miller.
The Great Internet Mersenne Prime Search (GIMPS) which has found the world's record for largest proven prime (274,207,281 - 1 as of June 2017), uses several algorithms, but these are primes in special forms. However the GIMPS page above does include some general deterministic primality tests. They appear to indicate that which algorithm is "fastest" depends upon the size of the number to be tested. If your number fits in 64 bits then you probably shouldn't use a method intended to work on primes of several million digits.
It depends on your application. There are some considerations:
- Do you need just the information whether a few numbers are prime, do you need all prime numbers up to a certain limit, or do you need (potentially) all prime numbers?
- How big are the numbers you have to deal with?
The Miller-Rabin and analogue tests are only faster than a sieve for numbers over a certain size (somewhere around a few million, I believe). Below that, using a trial division (if you just have a few numbers) or a sieve is faster.
This is an implementation of the Sieve of Eratosthenes in Python I've been toying with.
def eratosthenes(maximum: int) -> list[int | None]:
"""
Find all the prime numbers between 2 and `maximum`.
Args:
maximum: The maximum number to check.
Returns:
A list of primes between 2 and `maximum`.
"""
if maximum < 2:
return []
# Discard even numbers by default.
sequence = dict.fromkeys(range(3, maximum+1, 2), True)
for num, is_prime in sequence.items():
# Already filtered, let's skip it.
if not is_prime:
continue
# Avoid marking the same number twice.
for num2 in range(num ** 2, maximum+1, num):
# Here, `num2` might contain an even number - skip it.
if num2 in sequence:
sequence[num2] = False
# Re-add 2 as prime and filter out the composite numbers.
return [2] + [num for num, is_prime in sequence.items() if is_prime]
The code appears to take roughly 16s for 10000000 numbers on a humble Samsung Galaxy A40.
Suggestions are welcome!
It should be
-> list[int]. An empty list (that you probably refer to with the None?) is still a list of int. –
Hate You better replace
if num2 in sequence: by if num2 % 2:. This is significantly faster (and in my opinion better to read). –
Hate I found this solution pretty fast but it comes with consequences, So this is called Fermat's Little Theorem. If we take any number p and put that in (1^p)-1 or (2^p)-2...(n^p)-n likewise and the number we get is divisible by p then it's a prime number. Talking about consequences, it's not 100% right solution. There are some numbers like 341(not prime) it will pass the test with (2^341)-2 but fails on (3^341)-3, so it's called a composite number. We can have two or more checks to make sure they pass all of them. There is one more kind of number which are not prime but also pass all the test case:( 561, 1729 Ramanujan taxi no etc.
The good thing: With
(2^p)-2in first 25 billion numbers only 2183 fails this case.
#include <iostream>
#include <math.h>
using namespace std;
int isPrime(int p)
{
int tc = pow(2, p) - 2;
if (tc % p == 0)
{
cout << p << "is Prime ";
}
else
{
cout << p << "is Not Prime";
}
return 0;
}
int main()
{
int p;
cin >> p;
isPrime(p);
return 0;
}
Another Python implementation that is more straightforward and slightly faster* than the one in the answer of Death Mask Salesman:
import numpy as np
def prime_numbers(limit: int) -> list[int]:
"""Provide a list of all prime numbers <= the limit."""
is_prime = np.full((limit + 1, ), True)
is_prime[0:2] = False
for n in range(2, limit + 1):
if is_prime[n]:
is_prime[n**2::n] = False
return list(np.where(is_prime)[0])
You could further optimize by, e.g., excluding the 2, or by hard-coding even more prime numbers, but I wanted to keep it simple.
*exemplary runtime comparison (note: I used the optimized form of the other implementation, see my comment):
It looks like the "Generalized Sieve of Eratosthenes", but with Numpy instead of a List holding a loop as an output. –
Mondrian
@AfolabiOlaoluwa Yes, it is just a new implementation, not a new algorithm –
Hate
You may have been confused by "other (erastothenes)" - it is just referring to the function declaration from Death Mask Salesman (
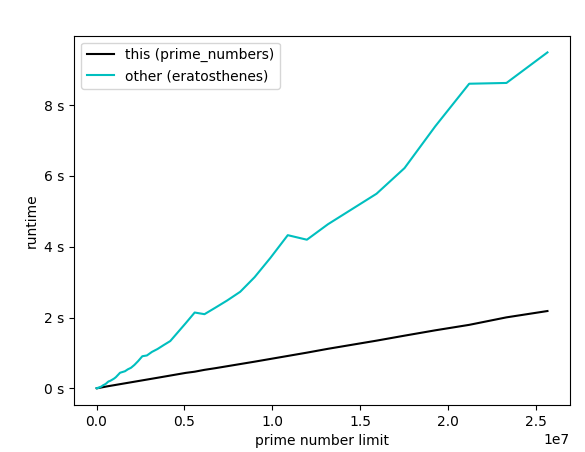
def erastothenes, while mine is def prime_numbers). –
Hate i wrote it today in C,compiled with tcc, figured out during preparation of compititive exams several years back. don't know if anyone already have wrote it alredy. it really fast(but you should decide whether it is fast or not). took one or two minuts to findout about 1,00,004 prime numbers between 10 and 1,00,00,000 on i7 processor with average 32% CPU use. as you know, only those can be prime which have last digit either 1,3,7 or 9 and to check if that number is prime or not, you have to divide that number by previously found prime numbers only. so first take group of four number = {1,3,7,9}, test it by dividing by known prime numbers, if reminder is non zero then number is prime, add it to prime number array. then add 10 to group so it becomes {11,13,17,19} and repeat the process.
#include <stdio.h>
int main() {
int nums[4]={1,3,7,9};
int primes[100000];
primes[0]=2;
primes[1]=3;
primes[2]=5;
primes[3]=7;
int found = 4;
int got = 1;
int m=0;
int upto = 1000000;
for(int i=0;i<upto;i++){
//printf("iteration number: %d\n",i);
for(int j=0;j<4;j++){
m = nums[j]+10;
//printf("m = %d\n",m);
nums[j] = m;
got = 1;
for(int k=0;k<found;k++){
//printf("testing with %d\n",primes[k]);
if(m%primes[k]==0){
got = 0;
//printf("%d failed for %d\n",m,primes[k]);
break;
}
}
if(got==1){
//printf("got new prime: %d\n",m);
primes[found]= m;
found++;
}
}
}
printf("found total %d prime numbers between 1 and %d",found,upto*10);
return 0;
}
I recently wrote this code to find the sum of numbers. It can be easily modified to find if a number is prime or not instead. Benchmarks are on top of the code.
// built on core-i2 e8400
// Benchmark from PowerShell
// Measure-Command { ExeName.exe }
// Days : 0
// Hours : 0
// Minutes : 0
// Seconds : 23
// Milliseconds : 516
// Ticks : 235162598
// TotalDays : 0.00027217893287037
// TotalHours : 0.00653229438888889
// TotalMinutes : 0.391937663333333
// TotalSeconds : 23.5162598
// TotalMilliseconds : 23516.2598
// built with latest MSVC
// cl /EHsc /std:c++latest main.cpp /O2 /fp:fast /Qpar
#include <cmath>
#include <iostream>
#include <vector>
inline auto prime = [](std::uint64_t I, std::vector<std::uint64_t> &cache) -> std::uint64_t {
std::uint64_t root{static_cast<std::uint64_t>(std::sqrtl(I))};
for (std::size_t i{}; cache[i] <= root; ++i)
if (I % cache[i] == 0)
return 0;
cache.push_back(I);
return I;
};
inline auto prime_sum = [](std::uint64_t S) -> std::uint64_t {
std::uint64_t R{5};
std::vector<std::uint64_t> cache;
cache.reserve(S / 16);
cache.push_back(3);
for (std::uint64_t I{5}; I <= S; I += 8)
{
std::uint64_t U{I % 3};
if (U != 0)
R += prime(I, cache);
if (U != 1)
R += prime(I + 2, cache);
if (U != 2)
R += prime(I + 4, cache);
R += prime(I + 6, cache);
}
return R;
};
int main()
{
std::cout << prime_sum(63210123);
}
This is the fastest algorithm to find all prime numbers from 1 to n(on my pc it found all from 1 to 1000000 just for 0.004 seconds).
#include <iostream>
#include <fstream>
using namespace std;
double FindPrime(bool* array, int size){
clock_t start;
double runtime;
for (int i = 2; i < size; i++)
array[i] = true;
start = clock();
for (int i = 2; i <= size; i++)
if (array[i])
for (int j = 2 * i; j < size; j += i)
array[j] = false;
runtime = (double)(clock() - start) / CLOCKS_PER_SEC;
return runtime;
}
int main() {
ofstream fout("prime.txt");
int n = 0;
cout << "Enter the upper limit of prime numbers searching algorithm:";
cin >> n;
bool* array = new bool[n + 1];
double duration = FindPrime(array, n + 1);
printf("\n%f seconds.\n", duration);
for (int i = 2; i <= n; i++)
if (array[i])
fout << i << endl;
fout.close();
return 0;
}
I always use this method for calculating primes numbers following with the sieve algorithm.
void primelist()
{
for(int i = 4; i < pr; i += 2) mark[ i ] = false;
for(int i = 3; i < pr; i += 2) mark[ i ] = true; mark[ 2 ] = true;
for(int i = 3, sq = sqrt( pr ); i < sq; i += 2)
if(mark[ i ])
for(int j = i << 1; j < pr; j += i) mark[ j ] = false;
prime[ 0 ] = 2; ind = 1;
for(int i = 3; i < pr; i += 2)
if(mark[ i ]) ind++; printf("%d\n", ind);
}
solution to find factors:
def divisors(integer):
result = set()
i = 2
j = integer/2
while(i <= j):
if integer % i == 0:
result.add(i)
#it dont need to
result.add(integer//i)
i += 1
j = integer//i
if len(result) > 0:
return f"not prime {sorted(result)}"
else:
return f"{integer} is prime"
--- Tests ---- import time
start_time = time.time()
print(divisors(180180180180))
print("--- %s seconds ---" % (time.time() - start_time))
--- 0.06314539909362793 seconds ---
start_time = time.time()
print(divs(180180180180180))
print("--- %s seconds ---" % (time.time() - start_time))
--- 1.5997519493103027 seconds ---
start_time = time.time()
print(divisors(1827))
print("--- %s seconds ---" % (time.time() - start_time))
--- 0.0 seconds ---
start_time = time.time()
print(divisors(104729))
print("--- %s seconds ---" % (time.time() - start_time))
--- 0.0 seconds ---
with this code:
def divs(integer):
result = set()
i = 2
j = integer / 2
loops = 0
while (i <= j):
if integer % i == 0:
print(f"loops:{loops}")
return f"{integer} is not a prime"
i += 1
j = integer // i
loops += 1
print(f"loops:{loops}")
return f"{integer} is prime"
--- Tests ---
start_time = time.time()
print(divs(180180180180180180180180))
print("--- %s seconds ---" % (time.time() - start_time))
--- 0.0 seconds ---
#include<stdio.h>
main()
{
long long unsigned x,y,b,z,e,r,c;
scanf("%llu",&x);
if(x<2)return 0;
scanf("%llu",&y);
if(y<x)return 0;
if(x==2)printf("|2");
if(x%2==0)x+=1;
if(y%2==0)y-=1;
for(b=x;b<=y;b+=2)
{
z=b;e=0;
for(c=2;c*c<=z;c++)
{
if(z%c==0)e++;
if(e>0)z=3;
}
if(e==0)
{
printf("|%llu",z);
r+=1;
}
}
printf("|\n%llu outputs...\n",r);
scanf("%llu",&r);
}
r is used prior to be initialized –
Straightforward
#include <iostream>
using namespace std;
int set [1000000];
int main (){
for (int i=0; i<1000000; i++){
set [i] = 0;
}
int set_size= 1000;
set [set_size];
set [0] = 2;
set [1] = 3;
int Ps = 0;
int last = 2;
cout << 2 << " " << 3 << " ";
for (int n=1; n<10000; n++){
int t = 0;
Ps = (n%2)+1+(3*n);
for (int i=0; i==i; i++){
if (set [i] == 0) break;
if (Ps%set[i]==0){
t=1;
break;
}
}
if (t==0){
cout << Ps << " ";
set [last] = Ps;
last++;
}
}
//cout << last << endl;
cout << endl;
system ("pause");
return 0;
}
this should be an answer on "How to write unstructured code without actually using GOTO". All this confuscation just to code a simple trial division!
(n%2)+1+(3*n) is kind of nice though. :) –
Cothran @Will Ness I would've downvoted this as an answer to that question; why use a for loop when a macro will do? :) –
Sabin
I know it's somewhat later, but this could be useful to people arriving here from searches. Anyway, here's some JavaScript that relies on the fact that only prime factors need to be tested, so the earlier primes generated by the code are re-used as test factors for later ones. Of course, all even and mod 5 values are filtered out first. The result will be in the array P, and this code can crunch 10 million primes in under 1.5 seconds on an i7 PC (or 100 million in about 20). Rewritten in C it should be very fast.
var P = [1, 2], j, k, l = 3
for (k = 3 ; k < 10000000 ; k += 2)
{
loop: if (++l < 5)
{
for (j = 2 ; P[j] <= Math.sqrt(k) ; ++j)
if (k % P[j] == 0) break loop
P[P.length] = k
}
else l = 0
}
This will give you lots of troubles if you are generating a big number of primes, and for the comparations, better use P[j]*P[j] <= k, because sqrt is pretty slow –
Correctitude
@Correctitude
sqrt can be hoisted out of the loop and computed only once, while P[j]*P[j] must be computed at every iteration. I wouldn't presume one is faster than the other without testing. –
Counterpoison The approach with sqrt outside the loop can definitely be faster if instead of precise sqrt you calculate a simple approximation that rounds it up to a near integer. Regardless,
k % P[j] in the inner-most loop makes the algorithm one of slower ones. –
Humus #include<iostream>
using namespace std;
void main()
{
int num,i,j,prime;
cout<<"Enter the upper limit :";
cin>>num;
cout<<"Prime numbers till "<<num<<" are :2, ";
for(i=3;i<=num;i++)
{
prime=1;
for(j=2;j<i;j++)
{
if(i%j==0)
{
prime=0;
break;
}
}
if(prime==1)
cout<<i<<", ";
}
}
this is about the slowest you can go about it. –
Cothran
This is very slow,if the upper limit is lets say 10000000 then this code will consume lot of time!! –
Waterman
this code is O(N^2/log N). without
break; it would be even slower, O(N^2), but that could be seen as a coding error already. saving and testing by primes is O(N^2/(log N)^2), and testing by primes below number's square root only, is O(N^1.5/(log N)^2). –
Cothran @WillNess Perhaps a bit hyperbolic. He could easily have started the for loop from 1 instead of 2, and added a j<=i instead of j<i. :) –
Sheepish
I don't think this post should be deleted, it serves as a valuable counterexample. –
Cothran
@KennyCason that would just break the code though. but yeah, since then I saw much slower codes, e.g.
[n | n<-[2..], notElem(n) [j*k | j<-[2..(n-1)], k<-[2..(n-1)]]], or the absolute winner, let { isPrime(n) = n>1 && []==[i | i<-[2..n-1], isPrime(i) && rem(n)(i)==0] } in filter(isPrime) [2..] (in Haskell, sorry; using list comprehension syntax; rem is for remainder, %; [] is empty list). Compared to these two, the one here is all right (and by the way, equivalent to the last one, if one crucial - and simple - change is made). –
Cothran @WillNess nice haha, I also code in Haskell so I can read that. :) –
Sheepish
© 2022 - 2024 — McMap. All rights reserved.
int p[]= {2, 3};qualify as a "fastest algorithm to find out primes" ? – Bendicty