I know this question has been seen as solved, but actually there is a super elegant solution to this, in only a few lines as follow. Such computation is precise, without any sort of numerical optimization.
## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)
E <- eigen(A, symmetric = TRUE) ## symmetric eigen decomposition
U <- E[[2]] ## eigen vectors, i.e., rotation matrix
D <- sqrt(E[[1]]) ## root eigen values, i.e., scaling factor
r <- 1.44 ## radius of original circle
Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r)) ## original vertices on major / minor axes
Z <- tcrossprod(Z * rep(D, each = 4), U) ## transformed vertices on major / minor axes
# [,1] [,2]
#[1,] -5.055136 6.224212
#[2,] -4.099908 -3.329834
#[3,] 5.055136 -6.224212
#[4,] 4.099908 3.329834
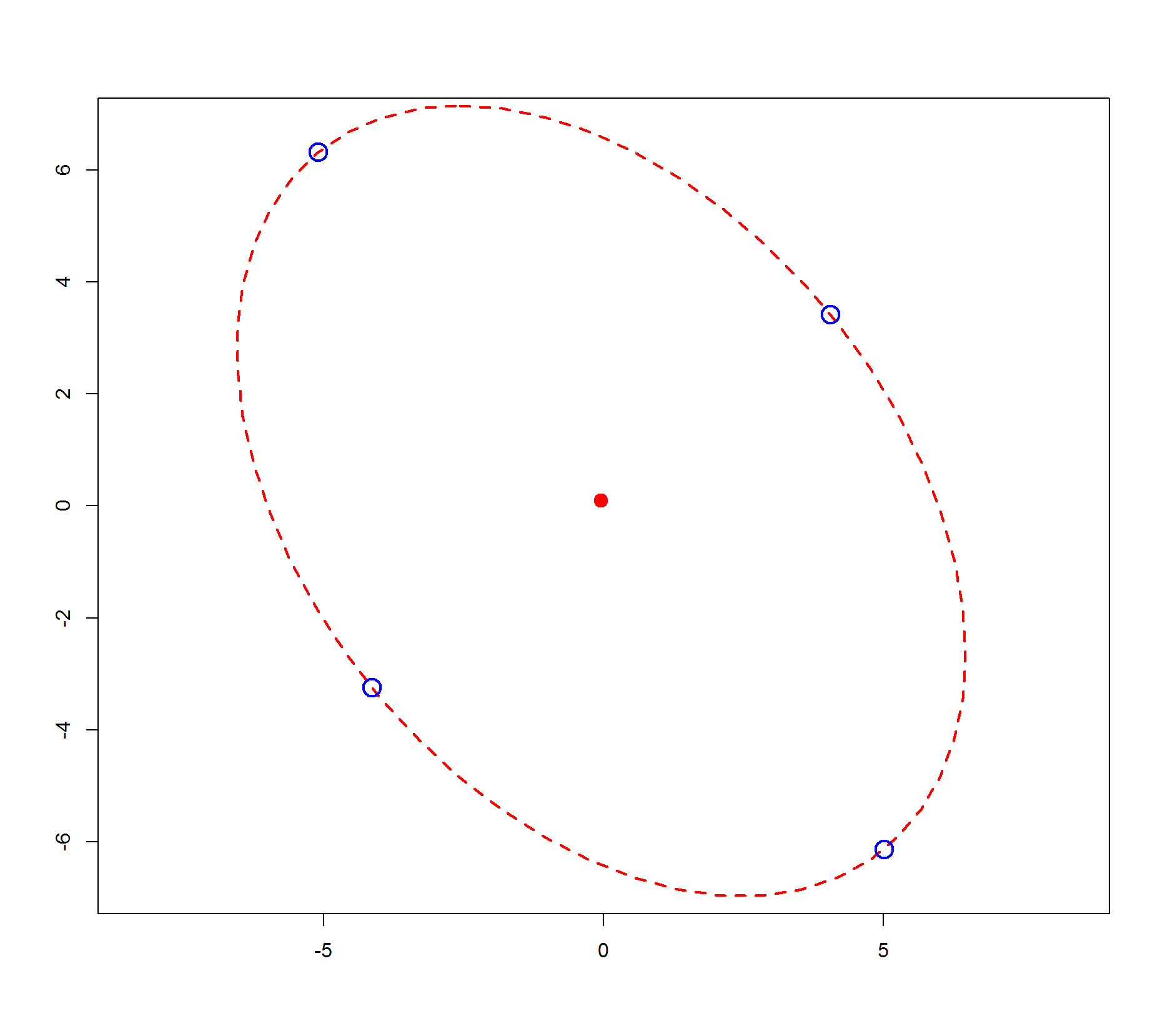
C0 <- c(-0.05, 0.09) ## new centre
Z <- Z + rep(C0, each = 4) ## shift to new centre
# [,1] [,2]
#[1,] -5.105136 6.314212
#[2,] -4.149908 -3.239834
#[3,] 5.005136 -6.134212
#[4,] 4.049908 3.419834
In order to explain the mathematics behind, I am going to take 3 steps:
- Where does this Ellipse come from?
- Cholesky decomposition method and its drawback.
- Eigen decomposition method and its natural interpretation.
Where does this ellipse comes from?
![Analytical form of the ellipse]()
In practice, this ellipse can be obtained by some linear transformation to the unit circle x ^ 2 + y ^ 2 = 1.
Cholesky decomposition method and its drawback
![Mathematics of Cholesky factorization]()
## initial circle
r <- 1.44
theta <- seq(0, 2 * pi, by = 0.01 * pi)
X <- r * cbind(cos(theta), sin(theta))
## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)
R <- chol(A) ## Cholesky decomposition
X1 <- X %*% R ## linear transformation
Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r)) ## original vertices on major / minor axes
Z1 <- Z %*% R ## transformed coordinates
## different colour per quadrant
g <- floor(4 * (1:nrow(X) - 1) / nrow(X)) + 1
## draw ellipse
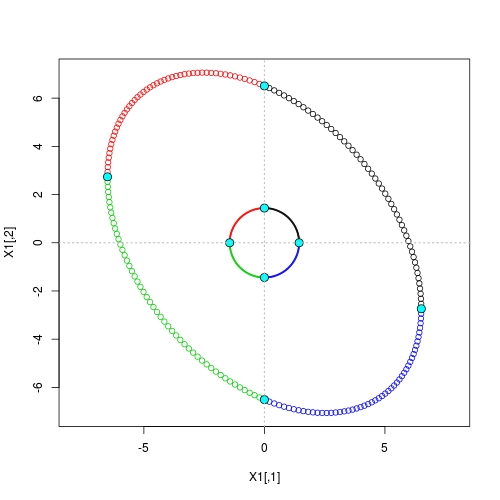
plot(X1, asp = 1, col = g)
points(Z1, cex = 1.5, pch = 21, bg = 5)
## draw circle
points(X, col = g, cex = 0.25)
points(Z, cex = 1.5, pch = 21, bg = 5)
## draw axes
abline(h = 0, lty = 3, col = "gray", lwd = 1.5)
abline(v = 0, lty = 3, col = "gray", lwd = 1.5)
![Geometry of Cholesky decomposition method]()
We see that the linear transform matrix R does not appear to have natural interpretation. The original vertices of the circle do not map to vertices of the ellipse.
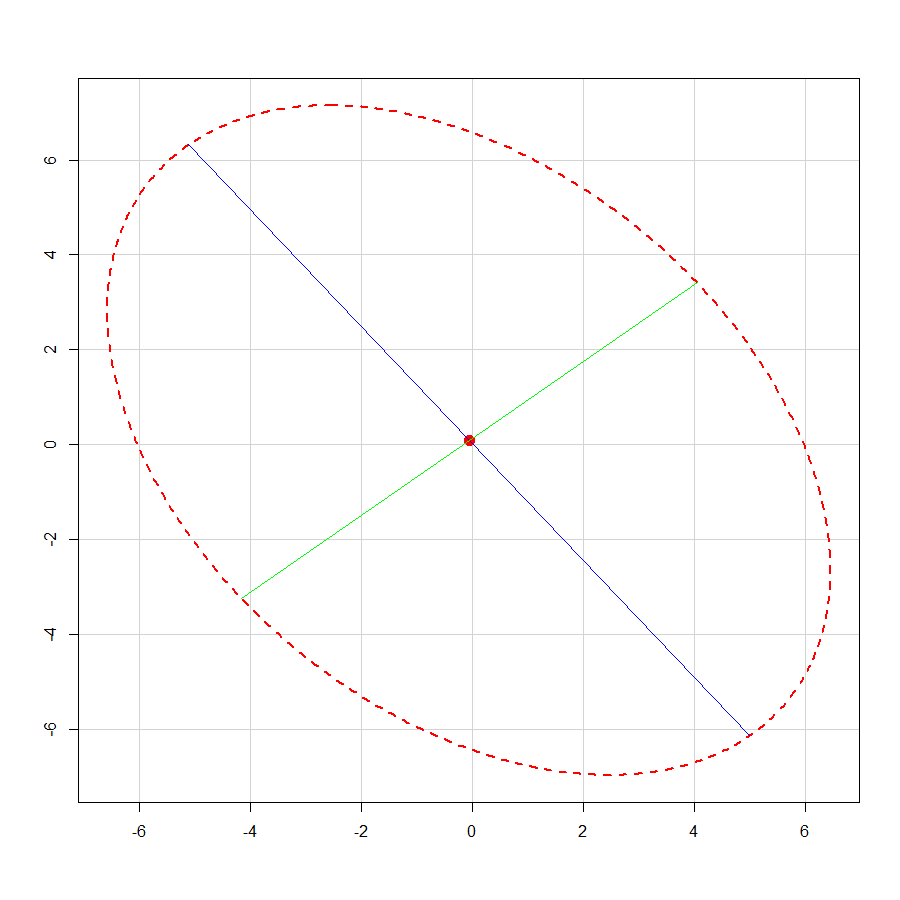
Eigen decomposition method and its natural interpretation
![Mathematics of Eigen decomposition]()
## initial circle
r <- 1.44
theta <- seq(0, 2 * pi, by = 0.01 * pi)
X <- r * cbind(cos(theta), sin(theta))
## target covariance matrix
A <- matrix(c(20.43, -8.59,-8.59, 24.03), nrow = 2)
E <- eigen(A, symmetric = TRUE) ## symmetric eigen decomposition
U <- E[[2]] ## eigen vectors, i.e., rotation matrix
D <- sqrt(E[[1]]) ## root eigen values, i.e., scaling factor
r <- 1.44 ## radius of original circle
Z <- rbind(c(r, 0), c(0, r), c(-r, 0), c(0, -r)) ## original vertices on major / minor axes
## step 1: re-scaling
X1 <- X * rep(D, each = nrow(X)) ## anisotropic expansion to get an axes-aligned ellipse
Z1 <- Z * rep(D, each = 4L) ## vertices on axes
## step 2: rotation
Z2 <- tcrossprod(Z1, U) ## rotated vertices on major / minor axes
X2 <- tcrossprod(X1, U) ## rotated ellipse
## different colour per quadrant
g <- floor(4 * (1:nrow(X) - 1) / nrow(X)) + 1
## draw rotated ellipse and vertices
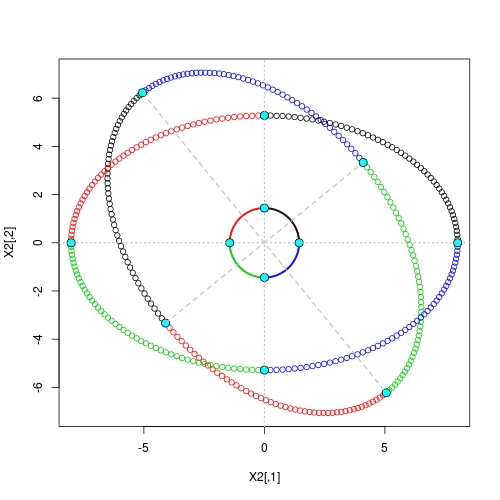
plot(X2, asp = 1, col = g)
points(Z2, cex = 1.5, pch = 21, bg = 5)
## draw axes-aligned ellipse and vertices
points(X1, col = g)
points(Z1, cex = 1.5, pch = 21, bg = 5)
## draw original circle
points(X, col = g, cex = 0.25)
points(Z, cex = 1.5, pch = 21, bg = 5)
## draw axes
abline(h = 0, lty = 3, col = "gray", lwd = 1.5)
abline(v = 0, lty = 3, col = "gray", lwd = 1.5)
## draw major / minor axes
segments(Z2[1,1], Z2[1,2], Z2[3,1], Z2[3,2], lty = 2, col = "gray", lwd = 1.5)
segments(Z2[2,1], Z2[2,2], Z2[4,1], Z2[4,2], lty = 2, col = "gray", lwd = 1.5)
![Geometry of Eigen decomposition]()
Here we see that in both stages of the transform, vertices are still mapped to vertices. It is exactly based on such property we have the neat solution given at the very beginning.


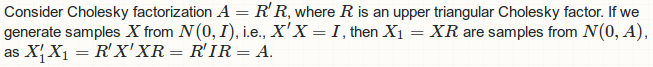

x<-ellipse(..)will give a matrix of coordinates inx, isn't what you're after ? – Commiserate