How to put a Python numpy array back together from diagonals obtained from splitting the array into right to left diagonals in first place?

Question

As I to my surprise failed to find a Python numpy method able to put an array split into its right to left diagonals in first place back together from the obtained diagonals, I have put some code together for this purpose, but have now hard time to arrive at the right algorithm. The code below works for the 4x3 array, but does not for the 3x5 and the other ones:

import numpy as np

def get_array(height, width):
    return np.arange(1, 1 + height*width).reshape(height, width)

array = get_array(5, 3)

print( array )
print("---", end="")
# Dimensions of a 2D array
N, M = array.shape
print(f" {N=} {M=} ", end="")
rangeNMbeg =    -M + 2  if N < M  else   -N + 1 
rangeNMend =      N + 1 if N < M  else    M 
flip = np.fliplr  # ( another one:  flipur )

diagonals = list( reversed ( [ np.diagonal( flip(array), offset=i) for i in range( rangeNMbeg, rangeNMend ) ] ) )
# Modification of each of diagonals (for example, double each first item)
print()
for diagonal in diagonals:
    pass
    #print(diagonal)
print("---")
# exit()
# Create a new array and arrange the diagonals back to the array
arrFromDiagonals = np.empty_like(array)

# Fill the array with the modified diagonals
for n in range(N): 
    row = []
    backCounter=0
    for m, diagonal in enumerate( diagonals[n : n + M  ] ) : 
        print(f"{str(diagonal):12s} {n=} {m=} len={len(diagonal)}", end = "  ")
        if len(diagonal) > m and n < M:
            print(f"len > m ", end = " > ")
            print(f"diagonal[{-1-m=}] = {diagonal[-1-m]}", end = "  ")
            row.append( diagonal[-1- m ])
        elif len(diagonal) == m :
            print(f"len===m ", end = " > ")
            print(f"diagonal[{0}] = {diagonal[0]}", end = "  ")
            row.append( diagonal[0] )
        else: 
            print(f"l <<< m ", end = " > ")
            print(f"diagonal[{-1}] = {diagonal[-1]}", end = "  ")
            row.append( diagonal[-1] )
        print(row)
    arrFromDiagonals[n,:] = np.array( row )
print(arrFromDiagonals)

and outputs:

[[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 13 12]
 [13 14 15]]

instead of

[[ 1  2  3],
 [ 4  5  6],
 [ 7  8  9],
 [10 11 12],
 [13 14 15]]

---

Wanted: a general approach to work on arrays using indices being one-based number of a diagonal (or anti-diagonal) and a one-based index of an element of the diagonal from the perspective of a diagonal root-element on the array edges. This approach will allow reading and writing the diagonals as easy as reading and writing rows and columns.

Hoi

better to provide an illustrative example to demonstrate what you want to do – Berri

And better to structure the code, create a "to diagonals" function and a "from diagonals" function if that's what it's doing (I think it is but I didn't really read it, the lack of an input example already turned me off). – Cyclorama

Answer 1

Numpy 1.25

Correcting the initial approach

First, let's make the initial approach work. There are two important parts: splitting the data into diagonals and merging them back together.

The smallest and largest diagonal offsets are -(hight-1) and width-1 respectively. So we can simplify splitting into diagonals as follows:

def get_diagonals(array):
    '''Return all the top-right to bottom-left diagonals of an array
    starting from the top-left corner.
    '''
    height, width = array.shape
    fliplr_arr = np.fliplr(array)
    return [fliplr_arr.diagonal(offset).copy()    # Starting in NumPy 1.9 diagonal returns a read-only view on the original array
            for offset in range(width-1, -height, -1)]

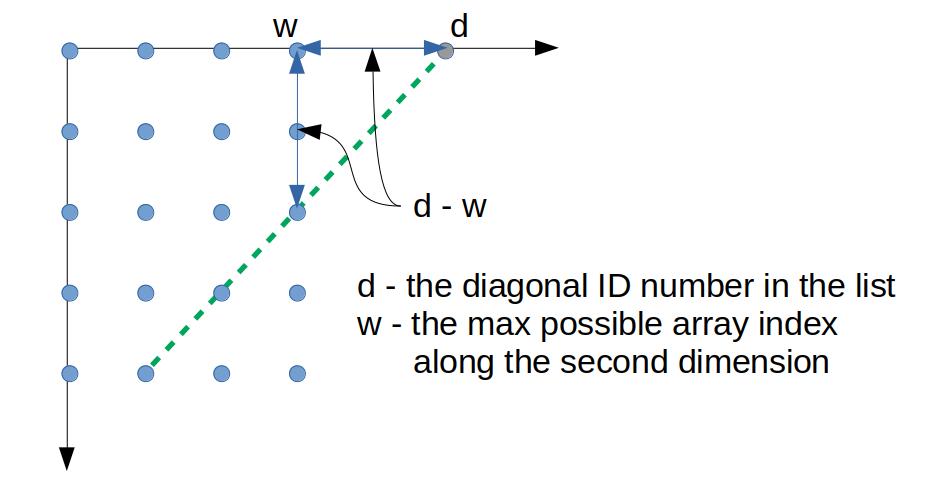
Having all diagonals collected in a list, let's numerate them by their index. Now, for all diagonals with index less then the array width, the index of an element within the diagonal is equal to its first index within the array. For other diagonals, a position of an element within the diagonal plus the height of the diagonal starting point gives the height of the element within the array. The diagonal starting point is equal to the difference of the diagonal number and the last possible index within the second array dimension (see the picture below).

So we can rewrite the second part of the code as follows:

def from_diagonals(diagonals, shape, dtype):
    arr = np.empty(shape, dtype)
    height, width = shape
    for h in range(height): 
        arr[h, :] = [
            diagonal[h if d < width else h - (d - (width-1))]
            for d, diagonal in enumerate(diagonals[h:h+width], start=h)
        ]
    return arr

Now the whole process of work is as follows:

arr = ...
diagonals = get_diagonals(arr)
for diag in diagonals:
    ...
new_arr = from_diagonals(diagonals, arr.shape, arr.dtype)

Working with indexes

We can create a function to reach data by the diagonal indexes like this:

def get_diagonal_function(height, width, base=0, antidiagonal=False):
    from functools import partial
    index = np.mgrid[:height, :width]
    if antidiagonal:
        index = index[..., ::-1]    # flip horizontal indices left-to-right
    _diag = partial(index.diagonal, axis1=1, axis2=2) 
    max_offset = width - 1
    shift = max_offset + base
    diagonal = lambda x: _diag(shift - x)
    diagonal.min = base
    diagonal.max = (height-1) + (width-1) + base
    diagonal.off = _diag
    return diagonal

Example of extracting all anti-diagonals:

diagonal = get_diagonal_function(*arr.shape, base=1, antidiagonal=True)
diagonals = [arr[*diagonal(x)] for x in range(diagonal.min, 1+diagonal.max)]
main_antidiagonal = diagonal.off(0)

Example of flipping data along anti-diagonals:

arr = [
    [ 1,  2,  4],
    [ 3,  5,  7],
    [ 6,  8, 10],
    [ 9, 11, 13],
    [12, 14, 15]
]
arr = np.array(arr)
diagonal = get_diagonal_function(*arr.shape, antidiagonal=True)

for x in range(1+diagonal.max):
    index = tuple(diagonal(x))
    arr[index] = arr[index][::-1]

print(arr)

[[ 1  3  6]
 [ 2  5  9]
 [ 4  8 12]
 [ 7 11 14]
 [10 13 15]]

Converting coordinates

Warning: The code below has not been properly tested; it is not intended for fast calculations; it is just an ad hoc proof of concept.

In case of anti-diagonals as described in the original post, converting can be performed as follows (see figure above for reference):

def diag_to_array(d, x, shape, direction='top-bottom,right-left'):
    height, width = shape
    h = x if d < width else x + (d - (width-1))
    w = d - h
    return h, w

In general, converting resembles an affine transformation (with cutting at the edges, if I may say so). But we need to know the direction and ordering of diagonals, of which there can be 16 options. They can be given by vectors indicating the direction of counting diagonals and elements along them. These vectors can also be used to determine a new origin.

def get_origin(d, e, shape):
    height, width = np.array(shape) - 1    # max coordinate values along dimensions
    match d, e:
        case ((1, x), (y, 1)) | ((x, 1), (1, y)):
            origin =  (0, 0)
        case ((1, x), (y, -1)) | ((x, -1), (1, y)):
            origin =  (0, width)
        case ((-1, x), (y, 1)) | ((x, 1), (-1, y)):
            origin =  (height, 0)
        case ((-1, x), (y, -1)) | ((x, -1), (-1, y)):
            origin =  (height, width)
    return np.array(origin)

Notes:

• d is one of the {(1, 0), (-1, 0), (0, 1), (0, -1)} vectors showing the direction of the diagonal number coordinate;
• e is one of the {(1, 1), (1, -1), (-1, 1), (-1, -1)} vectors showing the direction of numbering elements along the diagonal.

As for coordinate transformations, it seems more convenient to implement them in a class:

class Transfomer:
    def __init__(self, d, e, shape):
        self.d = np.array(d)
        self.e = np.array(e)
        self.shape = np.array(shape)
        self.A = np.stack([self.d, self.e])
        self.origin = get_origin(d, e, shape)
        self.edge = abs(self.d @ self.shape) - 1
        
    def diag_to_array(self, ndiagonal, element):
        '''Return the array coordiantes where:
        ndiagonal: the number of a diagonal
        element: the element index on the diagonal
        '''
        if ndiagonal > self.edge:
            element = element + ndiagonal - self.edge
        elif ndiagonal < 0:
            element = element - ndiagonal
        diag_coords = np.array([ndiagonal, element])
        array_coords = diag_coords @ self.A + self.origin
        return array_coords

    def array_to_diag(self, *args, **kwargs):
        raise NotImplementedError

Example:

d = (0, 1)     # take anti-diagonals from left to right starting from the top-left corner
e = (1, -1)    # and index their elements from top-right to bottom-left
arr = np.arange(5*3).reshape(5, 3)
coords = Transfomer(d, e, arr.shape)

diagonal = get_diagonal_function(*arr.shape, base=1, antidiagonal=True)
diagonals = [arr[*diagonal(x)] for x in range(diagonal.min, 1+diagonal.max)]

for ndiag, element in [(0, 0), (2, 1), (3, 0), (5, 1), (6, 0)]:
    array_point = coords.diag_to_array(ndiag, element)
    try:
        assert diagonals[ndiag][element] == arr[*array_point], f'{ndiag=}, {element=}'
    except AssertionError as e:
        print(e)        

Working with diagonals as a writeable view

If the array structure is straight simple (i.e. a contiguous sequence of data with no stride tricks or complicated transpositions), we can try (with some caution) to force a diagonal view to be writeable. Then all changes will be made with the original data, and you don't have to reassemble the diagonals again. Let's do mirroring anti-diagonals, for example:

def diag_range(shape, asnumpy=False):
    '''Returns a sequence of numbers arranged diagonally
    in a given shape as separate diagonals
    '''
    diagonals = []
    dmin, dmax = min(shape), max(shape)
    start = 1
    for n in range(dmin):
        end = start + n +1
        diagonals.append([*range(start, end)])
        start = end
    for n in range(dmin, dmax):
        end = start + dmin
        diagonals.append([*range(start, end)])
        start = end
    for n in range(dmin-1, 0, -1):
        end = start + n 
        diagonals.append([*range(start, end)])
        start = end
    if asnumpy:
        from numpy import array
        diagonals = list(map(array, diagonals))
    return diagonals

def from_diagonals(diagonals, shape, dtype):
    '''Returns an array constructed by the given diagonals'''
    arr = np.empty(shape, dtype)
    height, width = shape
    for h in range(height): 
        row = []
        for w, diag in enumerate(diagonals[h:h+width], start=h): 
            index = h - (w >= width) * (w - (width-1))
            row.append(diag[index])
        arr[h, :] = row
    return arr

h, w = shape = (6,3)
arr = from_diagonals(diag_range(shape), shape, 'int')
print('Initial array:'.upper(), arr, '', sep='\n')

fliplr_arr = np.fliplr(arr)
diagonals = [fliplr_arr.diagonal(i) for i in range(-h+1, w)]
for d in diagonals:
    d.flags.writeable = True    # use with caution
    d[:] = d[::-1]
print('Array with flipped diagonals:'.upper(), arr, sep='\n')

INITIAL ARRAY:
[[ 1  2  4]
 [ 3  5  7]
 [ 6  8 10]
 [ 9 11 13]
 [12 14 16]
 [15 17 18]]

ARRAY WITH FLIPPED DIAGONALS:
[[ 1  3  6]
 [ 2  5  9]
 [ 4  8 12]
 [ 7 11 15]
 [10 14 17]
 [13 16 18]]

Gospel

Is the purpose of the complex code to circumvent the fact that np.diagonal() method in many numpy versions (in earlier and now in the later ones, where the intermediate versions allowed write access) returns a read-only view? – Hoi

IMO code complexity can arise either from improper modelling or because a problem that may seem simple is actually not so trivial. I daresay you have outlined a rather complex question. It has many degrees of freedom and extreme cases. So what seemed to be a simple affine transformation, which is easy to compute with NumPy, turned out to be complicated by exceptions at the edges. As for a read-only view, I think it's not a big problem unless you're trying to transform data in place. – Gospel

@oOosys If you're asking what package or tool is already doing all the hard work for you in this case, I'd say using the sparse matrices mentioned in other answers seems like a good fit. – Gospel

Why not showing how to use np.diagonal() view to write a diagonal back to the array? It is the most simple and straightforward way and most easy to understand, isn't it? Sparse arrays of scipy are there for another reason ... this does not apply here and if, it comes at the cost of adding many arrays with the disadvantage that this does not handle the case of strings and tuples as array values. Check out my comment to https://mcmap.net/q/1170025/-how-to-put-a-python-numpy-array-back-together-from-diagonals-obtained-from-splitting-the-array-into-right-to-left-diagonals-in-first-place . – Hoi

@oOosys You seem to know the answer, so I'd appreciate hearing it from you. At the moment, I think it would be right to focus on one question at a time. If OP is about working with 2 coordinate systems, then you have now at least one general line where to go. On the other hand, if OP is about an effective way to combine diagonals in a matrix, then you have an option with sparse matrices (take it of leave it) as well as your own approach now working correctly. But if you keep thinking of the problem in terms of your project, take a look at the update about np.diagonal. – Gospel

Each numpy array arr has flags you can view using arr.flags. Python versions differ setting the default value for the WRITEABLE flag of a np.diagonal() view. In most versions it is set to False preventing writing to diagView = np.diagonal(arr, k) view, but ... after arr.flags.writeable=True you can write to the view. In other words you can use np.diagonal() for both, extracting a diagonal and writing a diagonal to an array. – Hoi

OK ... I see from the updated question that you have found it out yourself :) . – Hoi

Answer 2

So, the number of diagonals is the length of the diagonals array, and the offsets are based on the number of columns. I came up with the following array of offsets:

offsets = np.arange(len(diagonals))[::-1]-(a.shape[0]-1)

Where a is your original array.

Then, you can create diagonals using scipy.sparse.diags (this works with non-square diagonals) and add them to a zeros array. The final result will then need to be flipped left to right (similar to your original code when generating the diagonals).

b = np.zeros_like(a)
for diagonal, offset in zip(diagonals, offsets):
    b += diags(diagonal, offset, shape=a.shape)
b = np.fliplr(b)

Westernmost

I added your sparse answer to my overlly-tedious answer, mainly as a way of thinking through this problem. Just from reading the OP's question, it was hard to visualize what he was trying to do. Clealry the sparse devs have spent a lot more time thinking about this that the core numpy. – Hasidism

Check it out yourself: np.diagonal() can be used for both purposes: to get the diagonal and to write the (maybe modified) diagonal to the array, right? – Hoi

Answer 3

It's hard to visualize what's happening just from reading your code and seeing the trunacated examples. You've been working with this for some time, but I (and probably most of your readers) haven't. So a lot off what follows may be obvious to you, but is new to someone who hasn't spent much time with diagonals.

I'm going to simplify things a bit - by starting with a square array, and taking the straightforward diagonals - no flipping and reversal.

In [78]: arr = np.arange(1,17).reshape(4,4)

In [79]: N, M = arr.shape
    ...: rangeNMbeg =    -M + 2  if N < M  else   -N + 1 
    ...: rangeNMend =      N + 1 if N < M  else    M
    ...: offsets = np.arange(rangeNMbeg, rangeNMend)
    ...: diagonals = [ np.diagonal(arr, offset=i) for i in offsets ]

In [80]: offsets
Out[80]: array([-3, -2, -1,  0,  1,  2,  3])

In [81]: diagonals
Out[81]: 
[array([13]),
 array([ 9, 14]),
 array([ 5, 10, 15]),
 array([ 1,  6, 11, 16]),
 array([ 2,  7, 12]),
 array([3, 8]),
 array([4])]

With this pairing of offsets and diagonals, np.diag(d,o) produces a (4,4) array, which can be summed to recreate the original:

In [82]: res = np.zeros_like(arr)
    ...: for o,d in zip(offsets, diagonals):
    ...:     res += np.diag(d,o)
    ...:     

In [83]: res
Out[83]: 
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12],
       [13, 14, 15, 16]])

The next question, can I generalize the original shape?

One problem with doing the same with a (5,3) array, is that some of the np.diag(d,o) are (5,5), one is (4,4), and the rest (3,3). np.diag does not allow us to specify the 2d array shape. I don't use the diagonal functions enough to know whether is one that will do that. It shouldn't be hard to 'reverse engineer' np.diag to make such an array.

Internally np.diag and np.diagflat use a mapping like

res[:n-k].flat[i::n+1] = v   # or
res.flat[fi] = v

So if res shape is not square, we have to work out the details of this flat mapping.

scipy.sparse

As @jared pointed out using scipy.sparse makes this easy. For the (5,3) case (no flips etc):

In [130]: offsets
Out[130]: array([-4, -3, -2, -1,  0,  1,  2])

In [131]: diagonals
Out[131]: 
[array([13]),
 array([10, 14]),
 array([ 7, 11, 15]),
 array([ 4,  8, 12]),
 array([1, 5, 9]),
 array([2, 6]),
 array([3])]

In [132]: from scipy import sparse    
In [133]: sparse.diags(diagonals, offsets, shape=(5,3)).A
Out[133]: 
array([[ 1.,  2.,  3.],
       [ 4.,  5.,  6.],
       [ 7.,  8.,  9.],
       [10., 11., 12.],
       [13., 14., 15.]])

Sparse matrices often have a strongly diagonal structure (e.g. in finite difference problems), so this package has a dia_matrix format

dia_matrix((data, offsets), shape=(M, N))

diags is a constructor that creates the correct data:

In [147]: M = sparse.diags(diagonals, offsets, shape=(5,3))    
In [148]: M
Out[148]: 
<5x3 sparse matrix of type '<class 'numpy.float64'>'
    with 15 stored elements (7 diagonals) in DIAgonal format>

In [149]: M.offsets
Out[149]: array([-4, -3, -2, -1,  0,  1,  2])

In [150]: M.data
Out[150]: 
array([[13.,  0.,  0.,  0.],
       [10., 14.,  0.,  0.],
       [ 7., 11., 15.,  0.],
       [ 4.,  8., 12.,  0.],
       [ 1.,  5.,  9.,  0.],
       [ 0.,  2.,  6.,  0.],
       [ 0.,  0.,  3.,  0.]])

Note that data is a square array, with the same values as the list of diagonals, but with some padding. The code that maps the list of diagonals to this padded data is python, and can be viewed as the np.diags [source].

sparse also has code to readily convert this dia_matrix format to csr which is used for most calculations. It also uses this conversion when rendering the matrix as a dense array.

Hasidism

This answer is misleading suggesting that there is no straightforward way to write the diagonals back to the array. Fact is that np.diagonal() can be used for both purposes: to get the diagonal from the array and to write a diagonal to the array. Be warned: "No matter the reputation the respondents can make mistakes - check important info." – Hoi

Answer 4

A straight forward solution is to access the diagonals with indexes. Accessing the entries directly with np.digonal is not possible as np.digonal changed two times at version 1.7 and 1.9. In addition to the other answers provided, this version also works with higher-dimensional arrays, not just 2D arrays. Furthermore, it does not require modifying the numpy flag parameter, which serves a specific purpose.

Solution Core Function

import numpy as np

def diagonal_indexes(shape, axis1=0, axis2=1, direction='normal'):
    idx_array = np.arange(np.prod(shape), dtype=int).reshape(shape)
    if direction == 'anti':
        idx_array = np.fliplr(idx_array)
    
    return {i: np.diagonal(idx_array, offset=i, axis1=axis1, axis2=axis2) for i in range(1-idx_array.shape[axis1], idx_array.shape[axis2])}

# diagonal_indexes((2,3))
# -> {-1: array([3]), 0: array([0, 4]), 1: array([1, 5]), 2: array([2])}

• This function returns a dictionary to facilitate easy access to the desired diagonals later.
• The dictionary keys represent the offsets for np.diagonal. Hence, 0 is the main diagonal or leading diagonal. This approach is applicable to arrays with more than two axes. Following the conventions of np.diagonal, axis1 and axis2 specify the 2-D sub-arrays from which the diagonals are extracted. Additionally, axis1 and axis2 determine the order of the diagonals, i.e., the offset.
• I'll use the normal and anti for the diagonal directions instead of left and right.

Example usage

Two examples illustrates its functionality.

Example 1: Writing diagonals

array = np.zeros((4,3))
dict_idx = diagonal_indexes(array.shape)


# access a single value: array.flat[dict_idx[idx_diagonal], idx_on_diagonal]
array.flat[dict_idx[0][1]] = 40
array.flat[dict_idx[-1][2]] = 10

# access a whole diagonal
array.flat[dict_idx[1]] = np.arange(len(dict_idx[1]))+1

print(array)
# [[ 0.  1.  0.]
#  [ 0. 40.  2.]
#  [ 0.  0.  0.]
#  [ 0.  0. 10.]]

Example 2: diagonal indexes

def get_array(*shape, **kwargs):
    return np.arange(np.prod(shape), **kwargs).reshape(shape)

array = get_array(5, 4)

for kwargs in [dict(direction='normal', axis1=0, axis2=1), 
               dict(direction='normal', axis1=1, axis2=0), 
               dict(direction='anti', axis1=0, axis2=1), 
               dict(direction='anti', axis1=1, axis2=0)]:
    for i, idx in diagonal_indexes(array.shape, **kwargs).items():
        array.flat[idx] = i
    
    out_str = str(kwargs)[1:-1].replace(': ','=').replace("'","")
    print(f"diagonal_indexes(array.shape, {out_str})", '\n', array)
    print()

gives:

diagonal_indexes(array.shape, direction=normal, axis1=0, axis2=1) 
 [[ 0  1  2  3]
 [-1  0  1  2]
 [-2 -1  0  1]
 [-3 -2 -1  0]
 [-4 -3 -2 -1]]

diagonal_indexes(array.shape, direction=normal, axis1=1, axis2=0) 
 [[ 0 -1 -2 -3]
 [ 1  0 -1 -2]
 [ 2  1  0 -1]
 [ 3  2  1  0]
 [ 4  3  2  1]]

diagonal_indexes(array.shape, direction=anti, axis1=0, axis2=1) 
 [[ 3  2  1  0]
 [ 2  1  0 -1]
 [ 1  0 -1 -2]
 [ 0 -1 -2 -3]
 [-1 -2 -3 -4]]

diagonal_indexes(array.shape, direction=anti, axis1=1, axis2=0) 
 [[-3 -2 -1  0]
 [-2 -1  0  1]
 [-1  0  1  2]
 [ 0  1  2  3]
 [ 1  2  3  4]]

Attack

See the with bounty awarded answer how to circumvent the write protection present in some of numpy versions (according to your answer: "Accessing the entries directly with np.diagonal is not possible"). – Hoi

The numpy flag parameter is typically there on purpose... but you are right, "not possible" is also not true. However changing the flag, it's more a workaournd or hack for me, rather than a proper solution. – Attack

I don't see it this way ... measures overcoming prevention of possible bad use by users with not enough experience are legal way to a "proper solution" and the numpy data structure is generally designed for manipulating it. The history of NumPy shows that this choice is a very deliberate one and changed over time multiple times. If you want to arrive at best possible solution it does not make sense to care about such "protection" measures ... doesn't it? – Hoi

If so, I would suggest to overload diagonal with a version that sets the flag accordingly and you can simply do `array.diagonal()[:] = 1' ;) – Attack