Rough Overview
In functional programming, a functor is essentially a construction of lifting ordinary unary functions (i.e. those with one argument) to functions between variables of new types. It is much easier to write and maintain simple functions between plain objects and use functors to lift them, then to manually write functions between complicated container objects. Further advantage is to write plain functions only once and then re-use them via different functors.
Examples of functors include arrays, "maybe" and "either" functors, futures (see e.g. https://github.com/Avaq/Fluture), and many others.
Illustration
Consider the function constructing the full person's name from the first and last names. We could define it like fullName(firstName, lastName) as function of two arguments, which however would not be suitable for functors that only deal with functions of one arguments. To remedy, we collect all the arguments in a single object name, which now becomes the function's single argument:
// In JavaScript notation
fullName = name => name.firstName + ' ' + name.lastName
Now what if we have many people in an array? Instead of manually go over the list, we can simply re-use our function fullName via the map method provided for arrays with short single line of code:
fullNameList = nameList => nameList.map(fullName)
and use it like
nameList = [
{firstName: 'Steve', lastName: 'Jobs'},
{firstName: 'Bill', lastName: 'Gates'}
]
fullNames = fullNameList(nameList)
// => ['Steve Jobs', 'Bill Gates']
That will work, whenever every entry in our nameList is an object providing both firstName and lastName properties. But what if some objects don't (or even aren't objects at all)? To avoid the errors and make the code safer, we can wrap our objects into the Maybe type (se e.g. https://sanctuary.js.org/#maybe-type):
// function to test name for validity
isValidName = name =>
(typeof name === 'object')
&& (typeof name.firstName === 'string')
&& (typeof name.lastName === 'string')
// wrap into the Maybe type
maybeName = name =>
isValidName(name) ? Just(name) : Nothing()
where Just(name) is a container carrying only valid names and Nothing() is the special value used for everything else. Now instead of interrupting (or forgetting) to check the validity of our arguments, we can simply reuse (lift) our original fullName function with another single line of code, based again on the map method, this time provided for the Maybe type:
// Maybe Object -> Maybe String
maybeFullName = maybeName => maybeName.map(fullName)
and use it like
justSteve = maybeName(
{firstName: 'Steve', lastName: 'Jobs'}
) // => Just({firstName: 'Steve', lastName: 'Jobs'})
notSteve = maybeName(
{lastName: 'SomeJobs'}
) // => Nothing()
steveFN = maybeFullName(justSteve)
// => Just('Steve Jobs')
notSteveFN = maybeFullName(notSteve)
// => Nothing()
Category Theory
A Functor in Category Theory is a map between two categories respecting composition of their morphisms. In a Computer Language, the main Category of interest is the one whose objects are types (certain sets of values), and whose morphisms are functions f:a->b from one type a to another type b.
For example, take a to be the String type, b the Number type, and f is the function mapping a string into its length:
// f :: String -> Number
f = str => str.length
Here a = String represents the set of all strings and b = Number the set of all numbers. In that sense, both a and b represent objects in the Set Category (which is closely related to the category of types, with the difference being inessential here). In the Set Category, morphisms between two sets are precisely all functions from the first set into the second. So our length function f here is a morphism from the set of strings into the set of numbers.
As we only consider the set category, the relevant Functors from it into itself are maps sending objects to objects and morphisms to morphisms, that satisfy certain algebraic laws.
Example: Array
Array can mean many things, but only one thing is a Functor -- the type construct, mapping a type a into the type [a] of all arrays of type a. For instance, the Array functor maps the type String into the type [String] (the set of all arrays of strings of arbitrary length), and set type Number into the corresponding type [Number] (the set of all arrays of numbers).
It is important not to confuse the Functor map
Array :: a => [a]
with a morphism a -> [a]. The functor simply maps (associates) the type a into the type [a] as one thing to another. That each type is actually a set of elements, is of no relevance here. In contrast, a morphism is an actual function between those sets. For instance, there is a natural morphism (function)
pure :: a -> [a]
pure = x => [x]
which sends a value into the 1-element array with that value as single entry. That function is not a part of the Array Functor! From the point of view of this functor, pure is just a function like any other, nothing special.
On the other hand, the Array Functor has its second part -- the morphism part. Which maps a morphism f :: a -> b into a morphism [f] :: [a] -> [b]:
// a -> [a]
Array.map(f) = arr => arr.map(f)
Here arr is any array of arbitrary length with values of type a, and arr.map(f) is the array of the same length with values of type b, whose entries are results of applying f to the entries of arr. To make it a functor, the mathematical laws of mapping identity to identity and compositions to compositions must hold, which are easy to check in this Array example.


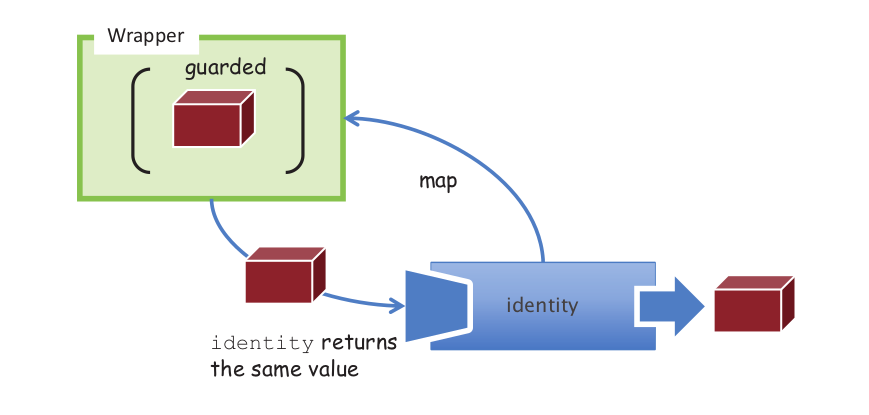
fmapmaps the functions. There is two kind of mappings involved. That way of seeing things will help to understand category theory (which is more general). I mean it's interesting to understand basic category theory to help us with all the category theory stuff in Haskell (functor, monads, ...). – Acicula