Here is a quicksort algorithm for numbers written in Clojure. It is basically the quicksort algorithm found in "The Joy of Clojure", 2nd edition, page 133. I modified it slightly for (hopefully) better readability, because the original felt a bit too compact:
(defn qsort-inner [work]
(lazy-seq
(loop [loopwork work]
(let [[ part & partz ] loopwork ]
(if-let [[pivot & valuez] (seq part)]
(let [ smaller? #(< % pivot)
smz (filter smaller? valuez)
lgz (remove smaller? valuez)
nxxt (list* smz pivot lgz partz) ]
(recur nxxt))
(if-let [[oldpivot & rightpartz] partz]
(cons oldpivot (qsort-inner rightpartz))
[]))))))
(defn qsort [ xs ]
(qsort-inner (list xs)))
The algorithm is started by a call to qsort, which envelops a passed list of numbers into another list (thus creating a list containing a single list), then calls qsort-inner.
(qsort [10 4 5 88 7 1]) ;; (qsort-inner [[10 4 5 88 7 1]])
;; (1 4 5 7 10 88)
qsort-inner has three noteworthy points:
- It delays actual processing. Instead of returning the result of a complete sorting of the input list, it returns a "lazy-seq", which is an (object? thing? thunk?) that emits the next number of the sorted sequence when queried, i.e. sorts on an as-needed basis. The state of the computation is given by the suspended tail of
(cons oldpivot (qsort-inner rightpartz)) - There is a
loop+recurtail-recursive part which is used whenever the algorithm wanders down the sorting tree "towards the left" (see below for algorithm details.) - There is a fully recursive call
(qsort-inner rightpartz)which is used when the next least number has been obtained and the sorting tree can be "re-arranged" (see below for algorithm details.)
With the help of the lazy-seq thing, we can make the algorithm emit data one-by-one:
;; the full result is generated on printout
(qsort [10 4 5 88 7 1])
(1 4 5 7 10 88)
;; store the lazy-seq and query it
(def l (qsort [10 4 5 88 7 1]))
(first l)
;; 1
(second l)
;; 4
I was thinking about how to perform this lazy quicksort in Prolog. In fact, laziness, at least in this instance, is given for free in Prolog by backtracking! We can ask for a first result, computation halts and the next result is then obtained by backtracking.
qsort_inner(X, [[],X|_]).
qsort_inner(X, [[],_|WorkRest]) :- qsort_inner(X, WorkRest).
qsort_inner(X, [[Piv|Ns]|WorkRest]) :-
pick_smaller(Piv,Ns,SMs),
pick_notsmaller(Piv,Ns,NSMs),
qsort_inner(X,[SMs,Piv,NSMs|WorkRest]).
pick_smaller(Pivot,Ins,Outs) :- include(@>(Pivot),Ins,Outs).
pick_notsmaller(Pivot,Ins,Outs) :- exclude(@>(Pivot),Ins,Outs).
qsort(X,Lin) :- qsort_inner(X,[Lin]).
Sort a list "lazily":
qsort(X,[3,2,1]).
X = 1;
X = 2;
X = 3;
false
Gotta get them all:
qsort_fully(Lin,Lout) :- bagof(X, qsort(X, Lin), Lout).
Unfortunately, the data structure that keeps track of the computational state is not apparent: it is on the stack, it cannot be unified to a variable. Thus is can only use this kind of "laziness" when I am on Prolog's top level.
How do I capture the state of the computation and invoke it later?
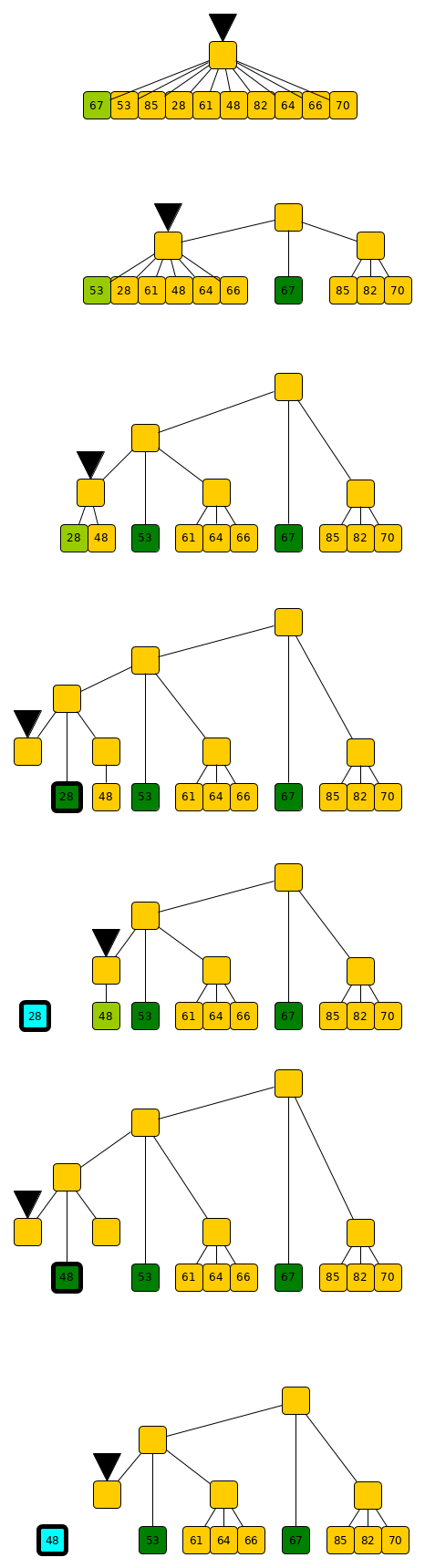
Note on how the quick sort works
- Given a list of numbers, the algorithm selects the first element of the list as pivot value (light green in the image).
- It then builds a tree with those numbers strictly smaller than the pivot value in a list "on the left", the pivot itself (dark green) and those numbers larger or equal to the pivot value as a list "on the right".
- It then recursively moves down this tree "towards the left".
- This continues until the list of numbers smaller than the pivot value is empty.
- At that point, the pivot value (here, 28) is the least number overall and can be output.
- This makes the list to sort one element smaller. The tree can now be reduced by one level with a trivial rearrangement operation: the right branch of the now left-branch-less and pivot-less "deepest tree-node but one" becomes the left branch of the tree node "deepest tree-node but two".
- Searching for the least element can now proceed again "towards the left".
The tree structure does not need to be explicitly kept as it holds no information. Instead, the sequence of alternating "leaf lists" and "pivot numbers" is kept in a list. Which is why we the intial "list of a lits of numbers".

freeze/2(also, gist.github.com/mndrix/4644762). Or some combination of the two. :) – Saltillonext/3-- the current state is also needed. :) (not so messy, I think.) – Saltillofreeze/2at the time. had to get by without it. :) – Saltillo