Circle-Rectangle collision detection (intersection)

Question

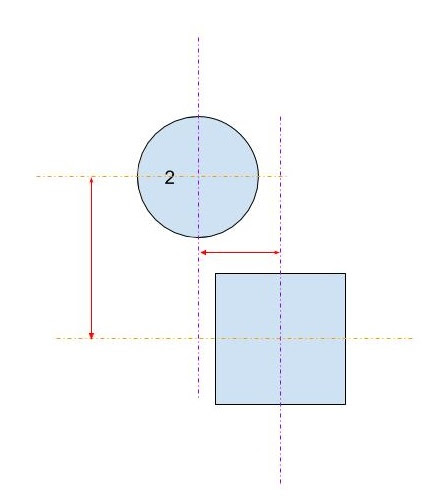
How can I tell whether a circle and a rectangle intersect in 2D Euclidean space? (i.e. classic 2D geometry)

Kellen

Is the rectangle always aligned with the axes, or can it be rotated by an arbitrary angle? – Trypsin

@eJames: how does it matter? You're checking the rectangle for intersection with a circle; you always can transform your coordinate system so that the rectangle is axis-parallel with no change in the circle :-) – Psychoneurotic

You should add that as an answer, rotating through -Θ and all... – Kellen

@ShreevatsaR: It matters in terms of wether or not I need to worry about that coordinate translation or not. @aib: Oh dear! – Trypsin

Answer 1

There are only two cases when the circle intersects with the rectangle:

• Either the circle's centre lies inside the rectangle, or
• One of the edges of the rectangle has a point in the circle.

Note that this does not require the rectangle to be axis-parallel.

(One way to see this: if none of the edges has a point in the circle (if all the edges are completely "outside" the circle), then the only way the circle can still intersect the polygon is if it lies completely inside the polygon.)

With that insight, something like the following will work, where the circle has centre P and radius R, and the rectangle has vertices A, B, C, D in that order (not complete code):

def intersect(Circle(P, R), Rectangle(A, B, C, D)):
    S = Circle(P, R)
    return (pointInRectangle(P, Rectangle(A, B, C, D)) or
            intersectCircle(S, (A, B)) or
            intersectCircle(S, (B, C)) or
            intersectCircle(S, (C, D)) or
            intersectCircle(S, (D, A)))

If you're writing any geometry you probably have the above functions in your library already. Otherwise, pointInRectangle() can be implemented in several ways; any of the general point in polygon methods will work, but for a rectangle you can just check whether this works:

0 ≤ AP·AB ≤ AB·AB and 0 ≤ AP·AD ≤ AD·AD

And intersectCircle() is easy to implement too: one way would be to check if the foot of the perpendicular from P to the line is close enough and between the endpoints, and check the endpoints otherwise.

The cool thing is that the same idea works not just for rectangles but for the intersection of a circle with any simple polygon — doesn't even have to be convex!

Psychoneurotic

Hmm, true. I started out with the simple (corner in circle) check and moved on to other cases from there. I did not see the simplification resulting from the fact that corners ARE points on the edges. – Kellen

For what it's worth, I really think this answer is better than mine. Two main reasons: 1: it does not require a rotation if the rectangle is not axis-parallel, and, 2: the concept easily extends to all polygons. – Trypsin

sorry, my bad. I was thinking about corners when you meant edges. – Cyder

If the rectangles are parallel though, e.James' solution is computationally more efficient. – Salazar

@paniq: Well, both are constant-time. :-) But yes, this is more useful as a general solution, covering rectangles with any orientation, and in fact any simple polygon. – Psychoneurotic

what about the case in which the rectangle is completely inside the circle, but the circle's center is not within the rectangle? – Hepza

@ericsoco: Good observation. :-) I guess I should have said "intersects the disc" in "one of the edges of the rectangle intersects the circle", because I meant means that it shares a point with the circle itself, not necessarily the circle's boundary. Anyway, the description above, "check if the foot of the perpendicular from P [the circle's centre] to the line is close enough and between the endpoints, and check the endpoints otherwise" will still work — e.g. the endpoints lie inside the circle (disc). – Psychoneurotic

@Psychoneurotic a circle is defined as the set of points equidistant from its center, so the "circle's boundary" == the circle...but i'm sure you know this already :) anyway, i get what you're saying about the endpoints inside the circle. thanks for the solid answer, and for verification it works in this case as well! – Hepza

To find a version of this answer made in the Python Programming language, go to https://mcmap.net/q/118868/-detecting-rectangle-collision-with-a-circle (from "Detecting Rectangle collision with a Circle", https://mcmap.net/q/118868/-detecting-rectangle-collision-with-a-circle/3787376) – Borsch

Sorry! Accident. Removed. Thanks for a helpful answer. – Criswell

What about part of circle (not including center) inside the middle of a wide rectangle? – Dah

@DexD.Hunter If the center of the circle is outside the rectangle, but a part of it is inside the rectangle, then necessarily one of the edges of the rectangle intersects the circle. – Psychoneurotic

@Psychoneurotic yep, the "edge". Sorry, I misunderstood what you have written – Dah

@DexD.Hunter No problem, as there was a chance of misunderstanding, I tweaked the wording and added some pictures. – Psychoneurotic

Could someone maybe provide example / pseudo code for intersectCircle? Thanks :) – Scabious

I find this answer distastefully overrated. Sure, it looks like it has fancy diagrams and code samples. But it's all smoke and mirrors explaining some obvious stuff, and then ultimately leaves the implementation as an exercise to the reader. If we had magical "lineIntersectsCircle" or "pointInRectangle" library functions, we'd probably already have "rectangleIntersectsCircle" function in that library as well! – Anglonorman

@PaulK You must be smarter than me. :-) It wasn't “obvious stuff” to me; I had to work out that checking these conditions was enough. Similarly it wasn't obvious how to implement pointInRectangle and intersectCircle; that's why I explained one possible way for implementing each of them, even though each has many ways (possibly answered on other questions). (BTW all this stuff is still not obvious to me; that's why the proof was added. The answer was written in 2008; I only added the pictures in 2017.) I was only sharing my understanding, and didn't intend to cause you any distaste. :-) – Psychoneurotic

love this answer! I completely missed the centerInRectangle check. It took me a second to realize why my game entities were sometimes not colliding! thanks! – Japheth

@PaulK I have thought about your comment several times, and I think I understand your perspective better. This answer was written in the early days of Stack Overflow (it entered public beta in Sep 2008), when the site as a community was focused on knowledge and ideas: many questions were more abstract, and we often wrote answers as enthusiasts trying to share our understanding. These days, I take it that many people visit StackOverflow to get solutions to problems they encounter at work, for which working code would be more useful, while conceptual understanding can be considered as unhelpful. – Psychoneurotic

you introduced pointInRectangle implementation, why not to do it for intersectCircle? – Boracite

Answer 2

Here is how I would do it:

bool intersects(CircleType circle, RectType rect)
{
    circleDistance.x = abs(circle.x - rect.x);
    circleDistance.y = abs(circle.y - rect.y);

    if (circleDistance.x > (rect.width/2 + circle.r)) { return false; }
    if (circleDistance.y > (rect.height/2 + circle.r)) { return false; }

    if (circleDistance.x <= (rect.width/2)) { return true; } 
    if (circleDistance.y <= (rect.height/2)) { return true; }

    cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +
                         (circleDistance.y - rect.height/2)^2;

    return (cornerDistance_sq <= (circle.r^2));
}

Here's how it works:

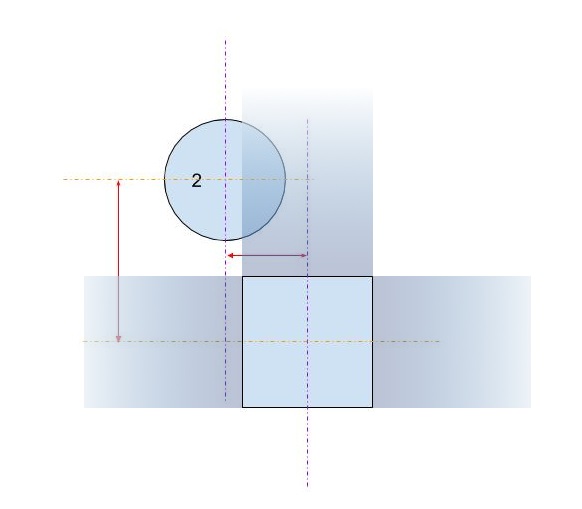
1. The first pair of lines calculate the absolute values of the x and y difference between the center of the circle and the center of the rectangle. This collapses the four quadrants down into one, so that the calculations do not have to be done four times. The image shows the area in which the center of the circle must now lie. Note that only the single quadrant is shown. The rectangle is the grey area, and the red border outlines the critical area which is exactly one radius away from the edges of the rectangle. The center of the circle has to be within this red border for the intersection to occur.

2. The second pair of lines eliminate the easy cases where the circle is far enough away from the rectangle (in either direction) that no intersection is possible. This corresponds to the green area in the image.

3. The third pair of lines handle the easy cases where the circle is close enough to the rectangle (in either direction) that an intersection is guaranteed. This corresponds to the orange and grey sections in the image. Note that this step must be done after step 2 for the logic to make sense.

4. The remaining lines calculate the difficult case where the circle may intersect the corner of the rectangle. To solve, compute the distance from the center of the circle and the corner, and then verify that the distance is not more than the radius of the circle. This calculation returns false for all circles whose center is within the red shaded area and returns true for all circles whose center is within the white shaded area.

Trypsin

Thank you, ShreevatsaR. I drew it with Photoshop because that was the only tool I had available on short notice :) – Trypsin

Very nice! Notes: apparently here, rect.x/y is at the upper right corner of the rectangle. Also you can eliminate the expensive square root, by instead comparing against the square of the radius. – Wort

Oh no, my bad. rect.x/y is at the lower left of the rectangle. I would have written: circleDistance.x = abs(circle.x - (rect.x + rect.width/2)); – Wort

I thought you had an error in your logic until I read into it further. Your third step should not say "This corresponds to the orange sections..." because that's not true. The third step only guarantees that if the center is inside the grey area the function will immediately end with true. The orange area and grey area was "safe" as soon as you passed step 2. Step 3 just allows you to bypass the expensive step 4. Which catches the rare corner case. But thank you this helped a lot. – Uniocular

If the center is in the orange area, step 3 will definitely return true. Step 3 will return true for everything in the grey and orange areas. It also simplifies step 4 by ensuring that the distance calculation is simply point-to-point (circle center to edge of rectangle). – Trypsin

Anyway, glad to hear that it was useful :) – Trypsin

@Trypsin Just wondering if you could upload the picture again. I've implemented your algorithm, and it works great; however, I also am checking for the case of whether the rectangle is completely inside the square and would like to see the diagram – Schaaff

@Tanner: That's weird. The internet appears to have eaten my illustration. I'm sure I have a copy of it somewhere. I'll look for it when I get home from work. – Trypsin

@Tanner: There we go. Hooray for backups and OCD ;) – Trypsin

just to clarify -- this answer applies only to axis-aligned rectangles. that's clear from reading through comments on other answers but not obvious from this answer+comments alone. (great answer for axis-aligned rects tho!) – Hepza

As some one wrote before, you need to change to: Math.Abs(circle.Center.X - (rectangle.X+rectangle.Width/2)) and same for y axis. But thank you very much for this great answer! – Urfa

This is just what I was looking for. No complicated loops, no handwaving, no "checking for X is trivial in geometry engines", just straight pseudocode and a great explanation. – Swipe

Bringing a bit tmore balanced load, I suggest you can subtract the half rect width & height back in the beginning. You burn 1 arithmetics if you hit the first "if", but you save 2 if you hit the last one. Thanks for the code, btw! – Digress

This is awesome. I just implemented in my game and it works great! thanks for the valuable information. – Aspect

Great! It's important for readers to know that here I believe the definition of a rect is rect.x & rect.y are the center of the rect. In my world a rect's xy is top/left of rect, and 0,0 is top/left of the screen, so I used: circleDistance_x = abs(circle.x - (rect.x-rect.w/2)); circleDistance_y = abs(circle.y - (rect.y-rect.h/2)); – Nordine

Very nice algorithm and great explanation. I have a slight qualm about the statement "o that the calculations do not have to be done four times". Direct comparisons and doing this in four quadrants might be on average theoretically more efficient as this code has two calls to abs(). Of course in reality this is intrinsic function and thus no call and in IEEE float abs is pretty fast op and it makes the code very easy to follow in 1st quadrant only. Well done. – Nuclei

Answer 3

Here is another solution that's pretty simple to implement (and pretty fast, too). It will catch all intersections, including when the sphere has fully entered the rectangle.

// clamp(value, min, max) - limits value to the range min..max

// Find the closest point to the circle within the rectangle
float closestX = clamp(circle.X, rectangle.Left, rectangle.Right);
float closestY = clamp(circle.Y, rectangle.Top, rectangle.Bottom);

// Calculate the distance between the circle's center and this closest point
float distanceX = circle.X - closestX;
float distanceY = circle.Y - closestY;

// If the distance is less than the circle's radius, an intersection occurs
float distanceSquared = (distanceX * distanceX) + (distanceY * distanceY);
return distanceSquared < (circle.Radius * circle.Radius);

With any decent math library, that can be shortened to 3 or 4 lines.

Lashundalasker

You have a bug in there, you search for closestY with Left and Right, not Top and Bottom, otherwise lovely solution. – Nevski

Ah, darn, that happens when you fix up code on-the-fly in Firefox :) Good find! – Lashundalasker

I like this answer the best. It's short, easy to understand, and fast. – Shan

I think that your solution fails if the rectangle is oblique to the x- and y-axes. – Perdue

@Perdue I think it's not hard to modify this algorithm to accommodate that case, one should simply apply a coordinate transformation where the origin is at the rectangle center and the rectangle isn't oblique anymore. You need to apply the transformation to the circle center only. – Fancied

This is basically the same as the code found at migapro.com/circle-and-rotated-rectangle-collision-detection which I've also ported to Objective-C. Works very well; it's a nice solution to the problem. – Novotny

< is valid if you're checking whether the area of intersection is 0, but in some use cases <= would be better, where a rectangle with a side tangent to a circle is considered to intersect it at a single point. Likewise, a circle with radius 0 within rectangle intersects it at a single point. – Prokopyevsk

I like this answer the best because it's easy to understand intuitively, step by step, without need for diagrams or the like. Also, the math operations are simple, so I expect it's about as fast as you could get it. (Anyone want to do a perf test between this and e.James' solution? I'm curious how they compare.) – Sapphism

@Lashundalasker shouldn't you be clamping circle.Y between rectnagle.Bottom and rectangle.Top (or do you assume Top has a lower Y value than Bottom)? – Townsfolk

Answer 4

The simplest solution I've come up with is pretty straightforward.

It works by finding the point in the rectangle closest to the circle, then comparing the distance.

You can do all of this with a few operations, and even avoid the sqrt function.

public boolean intersects(float cx, float cy, float radius, float left, float top, float right, float bottom)
{
   float closestX = (cx < left ? left : (cx > right ? right : cx));
   float closestY = (cy < top ? top : (cy > bottom ? bottom : cy));
   float dx = closestX - cx;
   float dy = closestY - cy;

   return ( dx * dx + dy * dy ) <= radius * radius;
}

And that's it! The above solution assumes an origin in the upper left of the world with the x-axis pointing down.

If you want a solution to handling collisions between a moving circle and rectangle, it's far more complicated and covered in another answer of mine.

Joby

This will fail to detect intersections if the circle radius is too small and its center is inside the rectangle! – Sonorous

Can you provide actual input that makes this fail? When the circle is inside, the left part of the test is 0.0. Unless the radius is zero the right part of the test should be > 0.0 – Joby

Will this work for rotated rectangles too ? if not then please give me a hint about that..... – Ivonne

Thanks man. It is working for me perfect. – Bias

what is the origin of the circle? in the top left or in the center? – Addison

This is basically the same as @Cygon's answer, but without the extra variables and comments. – Ullund

Answer 5

your sphere and rect intersect IIF
the distance between the circle-center and one vertex of your rect is smaller than the radius of your sphere
OR
the distance between the circle-center and one edge of your rect is smaller than the radius of your sphere ([point-line distance ])
OR
the circle center is inside the rect

point-point distance:

P1 = [x1,y1]
P2 = [x2,y2]
Distance = sqrt(abs(x1 - x2)+abs(y1-y2))

point-line distance:

L1 = [x1,y1],L2 = [x2,y2] (two points of your line, ie the vertex points)
P1 = [px,py] some point

Distance d =  abs( (x2-x1)(y1-py)-(x1-px)(y2-y1) ) / Distance(L1,L2)

circle center inside rect:
take an seperating axis aproach: if there exists a projection onto a line that seperates the rectangle from the point, they do not intersect

you project the point on lines parallel to the sides of your rect and can then easily determine if they intersect. if they intersect not on all 4 projections, they (the point and the rectangle) can not intersect.

you just need the inner-product ( x= [x1,x2] , y = [y1,y2] , x*y = x1*y1 + x2*y2 )

your test would look like that:

//rectangle edges: TL (top left), TR (top right), BL (bottom left), BR (bottom right)
//point to test: POI

seperated = false
for egde in { {TL,TR}, {BL,BR}, {TL,BL},{TR-BR} }:  // the edges
    D = edge[0] - edge[1]
    innerProd =  D * POI
    Interval_min = min(D*edge[0],D*edge[1])
    Interval_max = max(D*edge[0],D*edge[1])
    if not (  Interval_min ≤ innerProd ≤  Interval_max ) 
           seperated = true
           break  // end for loop 
    end if
end for
if (seperated is true)    
      return "no intersection"
else 
      return "intersection"
end if

this does not assume an axis-aligned rectangle and is easily extendable for testing intersections between convex sets.

Swordfish

Shouldn't the point to point distance be using a square, not an abs? – Lilliamlillian

Answer 6

This is the fastest solution:

public static boolean intersect(Rectangle r, Circle c)
{
    float cx = Math.abs(c.x - r.x - r.halfWidth);
    float xDist = r.halfWidth + c.radius;
    if (cx > xDist)
        return false;
    float cy = Math.abs(c.y - r.y - r.halfHeight);
    float yDist = r.halfHeight + c.radius;
    if (cy > yDist)
        return false;
    if (cx <= r.halfWidth || cy <= r.halfHeight)
        return true;
    float xCornerDist = cx - r.halfWidth;
    float yCornerDist = cy - r.halfHeight;
    float xCornerDistSq = xCornerDist * xCornerDist;
    float yCornerDistSq = yCornerDist * yCornerDist;
    float maxCornerDistSq = c.radius * c.radius;
    return xCornerDistSq + yCornerDistSq <= maxCornerDistSq;
}

Note the order of execution, and half the width/height is pre-computed. Also the squaring is done "manually" to save some clock cycles.

Culmination

I don’t think you can claim that five tests/comparisons in the most expensive code path is the “fastest solution” without some proof. – Towards

See en.wikipedia.org/wiki/Argumentum_ad_populum and en.wikipedia.org/wiki/Argument_from_ignorance – Towards

In my experience with this method, collision does not happen most of the time. Therefore the tests will cause an exit before before most of the code gets executed. – Culmination

Answer 7

Actually, this is much more simple. You need only two things.

First, you need to find four orthogonal distances from the circle centre to each line of the rectangle. Then your circle will not intersect the rectangle if any three of them are larger than the circle radius.

Second, you need to find the distance between the circle centre and the rectangle centre, then you circle will not be inside of the rectangle if the distance is larger than a half of the rectangle diagonal length.

Good luck!

Levin

Answer 8

If you are interested in a more graphical solution which even works on (in plane) rotated rectangles..

Demo: https://jsfiddle.net/exodus4d/94mxLvqh/2691/

The idea is:

1. Translate the scenary to the origin [0,0]
   • In case the rect is not in plane, the rotation center should be at [0, 0]
2. Rotate the scenary back into plane
3. Calculate intersection

const hasIntersection = ({x: cx, y: cy, r: cr}, {x, y, width, height}) => {
  const distX = Math.abs(cx - x - width / 2);
  const distY = Math.abs(cy - y - height / 2);

  if (distX > (width / 2 + cr)) {
    return false;
  }
  if (distY > (height / 2 + cr)) {
    return false;
  }

  if (distX <= (width / 2)) {
    return true;
  }
  if (distY <= (height / 2)) {
    return true;
  }

  const Δx = distX - width / 2;
  const Δy = distY - height / 2;
  return Δx * Δx + Δy * Δy <= cr * cr;
};

const rect = new DOMRect(50, 20, 100, 50);
const circ1 = new DOMPoint(160, 80);
circ1.r = 20;

const circ2 = new DOMPoint(80, 95);
circ2.r = 20;

const canvas = document.getElementById('canvas');
const ctx = canvas.getContext('2d');

ctx.strokeRect(rect.x, rect.y, rect.width, rect.height);

ctx.beginPath();
ctx.strokeStyle = hasIntersection(circ1, rect) ? 'red' : 'green';
ctx.arc(circ1.x, circ1.y, circ1.r, 0, 2 * Math.PI);
ctx.stroke();

ctx.beginPath();
ctx.strokeStyle = hasIntersection(circ2, rect) ? 'red' : 'green';
ctx.arc(circ2.x, circ2.y, circ2.r, 0, 2 * Math.PI);
ctx.stroke();

<canvas id="canvas"></canvas>

Tip: Instead of rotating the rect (4 points). You can rotate the circle (1 point) in opposite direction.

Houdon

How would it work with multiple rectangles & multiple circles ? – Weisbart

Answer 9

Here's my C code for resolving a collision between a sphere and a non-axis aligned box. It relies on a couple of my own library routines, but it may prove useful to some. I'm using it in a game and it works perfectly.

float physicsProcessCollisionBetweenSelfAndActorRect(SPhysics *self, SPhysics *actor)
{
    float diff = 99999;

    SVector relative_position_of_circle = getDifference2DBetweenVectors(&self->worldPosition, &actor->worldPosition);
    rotateVector2DBy(&relative_position_of_circle, -actor->axis.angleZ); // This aligns the coord system so the rect becomes an AABB

    float x_clamped_within_rectangle = relative_position_of_circle.x;
    float y_clamped_within_rectangle = relative_position_of_circle.y;
    LIMIT(x_clamped_within_rectangle, actor->physicsRect.l, actor->physicsRect.r);
    LIMIT(y_clamped_within_rectangle, actor->physicsRect.b, actor->physicsRect.t);

    // Calculate the distance between the circle's center and this closest point
    float distance_to_nearest_edge_x = relative_position_of_circle.x - x_clamped_within_rectangle;
    float distance_to_nearest_edge_y = relative_position_of_circle.y - y_clamped_within_rectangle;

    // If the distance is less than the circle's radius, an intersection occurs
    float distance_sq_x = SQUARE(distance_to_nearest_edge_x);
    float distance_sq_y = SQUARE(distance_to_nearest_edge_y);
    float radius_sq = SQUARE(self->physicsRadius);
    if(distance_sq_x + distance_sq_y < radius_sq)   
    {
        float half_rect_w = (actor->physicsRect.r - actor->physicsRect.l) * 0.5f;
        float half_rect_h = (actor->physicsRect.t - actor->physicsRect.b) * 0.5f;

        CREATE_VECTOR(push_vector);         

        // If we're at one of the corners of this object, treat this as a circular/circular collision
        if(fabs(relative_position_of_circle.x) > half_rect_w && fabs(relative_position_of_circle.y) > half_rect_h)
        {
            SVector edges;
            if(relative_position_of_circle.x > 0) edges.x = half_rect_w; else edges.x = -half_rect_w;
            if(relative_position_of_circle.y > 0) edges.y = half_rect_h; else edges.y = -half_rect_h;   

            push_vector = relative_position_of_circle;
            moveVectorByInverseVector2D(&push_vector, &edges);

            // We now have the vector from the corner of the rect to the point.
            float delta_length = getVector2DMagnitude(&push_vector);
            float diff = self->physicsRadius - delta_length; // Find out how far away we are from our ideal distance

            // Normalise the vector
            push_vector.x /= delta_length;
            push_vector.y /= delta_length;
            scaleVector2DBy(&push_vector, diff); // Now multiply it by the difference
            push_vector.z = 0;
        }
        else // Nope - just bouncing against one of the edges
        {
            if(relative_position_of_circle.x > 0) // Ball is to the right
                push_vector.x = (half_rect_w + self->physicsRadius) - relative_position_of_circle.x;
            else
                push_vector.x = -((half_rect_w + self->physicsRadius) + relative_position_of_circle.x);

            if(relative_position_of_circle.y > 0) // Ball is above
                push_vector.y = (half_rect_h + self->physicsRadius) - relative_position_of_circle.y;
            else
                push_vector.y = -((half_rect_h + self->physicsRadius) + relative_position_of_circle.y);

            if(fabs(push_vector.x) < fabs(push_vector.y))
                push_vector.y = 0;
            else
                push_vector.x = 0;
        }

        diff = 0; // Cheat, since we don't do anything with the value anyway
        rotateVector2DBy(&push_vector, actor->axis.angleZ);
        SVector *from = &self->worldPosition;       
        moveVectorBy2D(from, push_vector.x, push_vector.y);
    }   
    return diff;
}

Jamille

Answer 10

To visualise, take your keyboard's numpad. If the key '5' represents your rectangle, then all the keys 1-9 represent the 9 quadrants of space divided by the lines that make up your rectangle (with 5 being the inside.)

1) If the circle's center is in quadrant 5 (i.e. inside the rectangle) then the two shapes intersect.

With that out of the way, there are two possible cases: a) The circle intersects with two or more neighboring edges of the rectangle. b) The circle intersects with one edge of the rectangle.

The first case is simple. If the circle intersects with two neighboring edges of the rectangle, it must contain the corner connecting those two edges. (That, or its center lies in quadrant 5, which we have already covered. Also note that the case where the circle intersects with only two opposing edges of the rectangle is covered as well.)

2) If any of the corners A, B, C, D of the rectangle lie inside the circle, then the two shapes intersect.

The second case is trickier. We should make note of that it may only happen when the circle's center lies in one of the quadrants 2, 4, 6 or 8. (In fact, if the center is on any of the quadrants 1, 3, 7, 8, the corresponding corner will be the closest point to it.)

Now we have the case that the circle's center is in one of the 'edge' quadrants, and it only intersects with the corresponding edge. Then, the point on the edge that is closest to the circle's center, must lie inside the circle.

3) For each line AB, BC, CD, DA, construct perpendicular lines p(AB,P), p(BC,P), p(CD,P), p(DA,P) through the circle's center P. For each perpendicular line, if the intersection with the original edge lies inside the circle, then the two shapes intersect.

There is a shortcut for this last step. If the circle's center is in quadrant 8 and the edge AB is the top edge, the point of intersection will have the y-coordinate of A and B, and the x-coordinate of center P.

You can construct the four line intersections and check if they lie on their corresponding edges, or find out which quadrant P is in and check the corresponding intersection. Both should simplify to the same boolean equation. Be wary of that the step 2 above did not rule out P being in one of the 'corner' quadrants; it just looked for an intersection.

Edit: As it turns out, I have overlooked the simple fact that #2 is a subcase of #3 above. After all, corners too are points on the edges. See @ShreevatsaR's answer below for a great explanation. And in the meanwhile, forget #2 above unless you want a quick but redundant check.

Kellen

Answer 11

This function detect collisions (intersections) between Circle and Rectangle. He works like e.James method in his answer, but this one detect collisions for all angles of rectangle (not only right up corner).

NOTE:

aRect.origin.x and aRect.origin.y are coordinates of bottom left angle of rectangle!

aCircle.x and aCircle.y are coordinates of Circle Center!

static inline BOOL RectIntersectsCircle(CGRect aRect, Circle aCircle) {

    float testX = aCircle.x;
    float testY = aCircle.y;

    if (testX < aRect.origin.x)
        testX = aRect.origin.x;
    if (testX > (aRect.origin.x + aRect.size.width))
        testX = (aRect.origin.x + aRect.size.width);
    if (testY < aRect.origin.y)
        testY = aRect.origin.y;
    if (testY > (aRect.origin.y + aRect.size.height))
        testY = (aRect.origin.y + aRect.size.height);

    return ((aCircle.x - testX) * (aCircle.x - testX) + (aCircle.y - testY) * (aCircle.y - testY)) < aCircle.radius * aCircle.radius;
}

Cockeyed

Answer 12

Improving a little bit the answer of e.James:

double dx = abs(circle.x - rect.x) - rect.w / 2,
       dy = abs(circle.y - rect.y) - rect.h / 2;

if (dx > circle.r || dy > circle.r) { return false; }
if (dx <= 0 || dy <= 0) { return true; }

return (dx * dx + dy * dy <= circle.r * circle.r);

This subtracts rect.w / 2 and rect.h / 2 once instead of up to three times.

Godavari

I strongly suspect that most modern compilers would (or at least could) automatically optimize the redundant calculations away for you. – Parochialism

martineau - No, I didn't join several calculations in only one, directly. I changed them to delete these extra calculations in the process. – Godavari

My point was that nowadays many compilers will likely optimize the machine-code generated so that calculation of dx and dy values only happens once (without you needing to do it like this explicitly). – Parochialism

Answer 13

Here is the modfied code 100% working:

public static bool IsIntersected(PointF circle, float radius, RectangleF rectangle)
{
    var rectangleCenter = new PointF((rectangle.X +  rectangle.Width / 2),
                                     (rectangle.Y + rectangle.Height / 2));

    var w = rectangle.Width  / 2;
    var h = rectangle.Height / 2;

    var dx = Math.Abs(circle.X - rectangleCenter.X);
    var dy = Math.Abs(circle.Y - rectangleCenter.Y);

    if (dx > (radius + w) || dy > (radius + h)) return false;

    var circleDistance = new PointF
                             {
                                 X = Math.Abs(circle.X - rectangle.X - w),
                                 Y = Math.Abs(circle.Y - rectangle.Y - h)
                             };

    if (circleDistance.X <= (w))
    {
        return true;
    }

    if (circleDistance.Y <= (h))
    {
        return true;
    }

    var cornerDistanceSq = Math.Pow(circleDistance.X - w, 2) + 
                                    Math.Pow(circleDistance.Y - h, 2);

    return (cornerDistanceSq <= (Math.Pow(radius, 2)));
}

Bassam Alugili

Disclosure

Answer 14

I've a method which avoids the expensive pythagoras if not necessary - ie. when bounding boxes of the rectangle and the circle do not intersect.

And it'll work for non-euclidean too:

class Circle {
 // create the bounding box of the circle only once
 BBox bbox;

 public boolean intersect(BBox b) {
    // test top intersect
    if (lat > b.maxLat) {
        if (lon < b.minLon)
            return normDist(b.maxLat, b.minLon) <= normedDist;
        if (lon > b.maxLon)
            return normDist(b.maxLat, b.maxLon) <= normedDist;
        return b.maxLat - bbox.minLat > 0;
    }

    // test bottom intersect
    if (lat < b.minLat) {
        if (lon < b.minLon)
            return normDist(b.minLat, b.minLon) <= normedDist;
        if (lon > b.maxLon)
            return normDist(b.minLat, b.maxLon) <= normedDist;
        return bbox.maxLat - b.minLat > 0;
    }

    // test middle intersect
    if (lon < b.minLon)
        return bbox.maxLon - b.minLon > 0;
    if (lon > b.maxLon)
        return b.maxLon - bbox.minLon > 0;
    return true;
  }
}

• minLat,maxLat can be replaced with minY,maxY and the same for minLon, maxLon: replace it with minX, maxX
• normDist ist just a bit faster method then the full distance calculation. E.g. without the square-root in euclidean space (or without a lot of other stuff for haversine): dLat=(lat-circleY); dLon=(lon-circleX); normed=dLat*dLat+dLon*dLon. Of course if you use that normDist method you'll need to do create a normedDist = dist*dist; for the circle

See the full BBox and Circle code of my GraphHopper project.

Synchrotron

Answer 15

I created class for work with shapes hope you enjoy

public class Geomethry {
  public static boolean intersectionCircleAndRectangle(int circleX, int circleY, int circleR, int rectangleX, int rectangleY, int rectangleWidth, int rectangleHeight){
    boolean result = false;

    float rectHalfWidth = rectangleWidth/2.0f;
    float rectHalfHeight = rectangleHeight/2.0f;

    float rectCenterX = rectangleX + rectHalfWidth;
    float rectCenterY = rectangleY + rectHalfHeight;

    float deltax = Math.abs(rectCenterX - circleX);
    float deltay = Math.abs(rectCenterY - circleY);

    float lengthHypotenuseSqure = deltax*deltax + deltay*deltay;

    do{
        // check that distance between the centerse is more than the distance between the circumcircle of rectangle and circle
        if(lengthHypotenuseSqure > ((rectHalfWidth+circleR)*(rectHalfWidth+circleR) + (rectHalfHeight+circleR)*(rectHalfHeight+circleR))){
            //System.out.println("distance between the centerse is more than the distance between the circumcircle of rectangle and circle");
            break;
        }

        // check that distance between the centerse is less than the distance between the inscribed circle
        float rectMinHalfSide = Math.min(rectHalfWidth, rectHalfHeight);
        if(lengthHypotenuseSqure < ((rectMinHalfSide+circleR)*(rectMinHalfSide+circleR))){
            //System.out.println("distance between the centerse is less than the distance between the inscribed circle");
            result=true;
            break;
        }

        // check that the squares relate to angles
        if((deltax > (rectHalfWidth+circleR)*0.9) && (deltay > (rectHalfHeight+circleR)*0.9)){
            //System.out.println("squares relate to angles");
            result=true;
        }
    }while(false);

    return result;
}

public static boolean intersectionRectangleAndRectangle(int rectangleX, int rectangleY, int rectangleWidth, int rectangleHeight, int rectangleX2, int rectangleY2, int rectangleWidth2, int rectangleHeight2){
    boolean result = false;

    float rectHalfWidth = rectangleWidth/2.0f;
    float rectHalfHeight = rectangleHeight/2.0f;
    float rectHalfWidth2 = rectangleWidth2/2.0f;
    float rectHalfHeight2 = rectangleHeight2/2.0f;

    float deltax = Math.abs((rectangleX + rectHalfWidth) - (rectangleX2 + rectHalfWidth2));
    float deltay = Math.abs((rectangleY + rectHalfHeight) - (rectangleY2 + rectHalfHeight2));

    float lengthHypotenuseSqure = deltax*deltax + deltay*deltay;

    do{
        // check that distance between the centerse is more than the distance between the circumcircle
        if(lengthHypotenuseSqure > ((rectHalfWidth+rectHalfWidth2)*(rectHalfWidth+rectHalfWidth2) + (rectHalfHeight+rectHalfHeight2)*(rectHalfHeight+rectHalfHeight2))){
            //System.out.println("distance between the centerse is more than the distance between the circumcircle");
            break;
        }

        // check that distance between the centerse is less than the distance between the inscribed circle
        float rectMinHalfSide = Math.min(rectHalfWidth, rectHalfHeight);
        float rectMinHalfSide2 = Math.min(rectHalfWidth2, rectHalfHeight2);
        if(lengthHypotenuseSqure < ((rectMinHalfSide+rectMinHalfSide2)*(rectMinHalfSide+rectMinHalfSide2))){
            //System.out.println("distance between the centerse is less than the distance between the inscribed circle");
            result=true;
            break;
        }

        // check that the squares relate to angles
        if((deltax > (rectHalfWidth+rectHalfWidth2)*0.9) && (deltay > (rectHalfHeight+rectHalfHeight2)*0.9)){
            //System.out.println("squares relate to angles");
            result=true;
        }
    }while(false);

    return result;
  } 
}

Winne

Answer 16

Here's a fast one-line test for this:

if (length(max(abs(center - rect_mid) - rect_halves, 0)) <= radius ) {
  // They intersect.
}

This is the axis-aligned case where rect_halves is a positive vector pointing from the rectangle middle to a corner. The expression inside length() is a delta vector from center to a closest point in the rectangle. This works in any dimension.

Facture

Answer 17

• First check if the rectangle and the square tangent to the circle overlaps (easy). If they do not overlaps, they do not collide.
• Check if the circle's center is inside the rectangle (easy). If it's inside, they collide.
• Calculate the minimum squared distance from the rectangle sides to the circle's center (little hard). If it's lower that the squared radius, then they collide, else they don't.

It's efficient, because:

• First it checks the most common scenario with a cheap algorithm and when it's sure they do not collide, it ends.
• Then it checks the next most common scenario with a cheap algorithm (do not calculate square root, use the squared values) and when it's sure they collide it ends.
• Then it executes the more expensive algorithm to check collision with the rectangle borders.

Muddle

Answer 18

worked for me (only work when angle of rectangle is 180)

function intersects(circle, rect) {
  let left = rect.x + rect.width > circle.x - circle.radius;
  let right = rect.x < circle.x + circle.radius;
  let top = rect.y < circle.y + circle.radius;
  let bottom = rect.y + rect.height > circle.y - circle.radius;
  return left && right && bottom && top;
}

Philosophy

hmmm... I voted this up but then tested properly and I think it does not work on the corners for instance. It would work for two rectangles. – Duet

Answer 19

Works, just figured this out a week ago, and just now got to testing it.

double theta = Math.atan2(cir.getX()-sqr.getX()*1.0,
                          cir.getY()-sqr.getY()*1.0); //radians of the angle
double dBox; //distance from box to edge of box in direction of the circle

if((theta >  Math.PI/4 && theta <  3*Math.PI / 4) ||
   (theta < -Math.PI/4 && theta > -3*Math.PI / 4)) {
    dBox = sqr.getS() / (2*Math.sin(theta));
} else {
    dBox = sqr.getS() / (2*Math.cos(theta));
}
boolean touching = (Math.abs(dBox) >=
                    Math.sqrt(Math.pow(sqr.getX()-cir.getX(), 2) +
                              Math.pow(sqr.getY()-cir.getY(), 2)));

Monobasic

Might work for Circle-Square, but the question is about Circle-Rectangle. – Parochialism

Answer 20

For those have to calculate Circle/Rectangle collision in Geographic Coordinates with SQL,
this is my implementation in oracle 11 of e.James suggested algorithm.

In input it requires circle coordinates, circle radius in km and two vertices coordinates of the rectangle:

CREATE OR REPLACE FUNCTION "DETECT_CIRC_RECT_COLLISION"
(
    circleCenterLat     IN NUMBER,      -- circle Center Latitude
    circleCenterLon     IN NUMBER,      -- circle Center Longitude
    circleRadius        IN NUMBER,      -- circle Radius in KM
    rectSWLat           IN NUMBER,      -- rectangle South West Latitude
    rectSWLon           IN NUMBER,      -- rectangle South West Longitude
    rectNELat           IN NUMBER,      -- rectangle North Est Latitude
    rectNELon           IN NUMBER       -- rectangle North Est Longitude
)
RETURN NUMBER
AS
    -- converts km to degrees (use 69 if miles)
    kmToDegreeConst     NUMBER := 111.045;

    -- Remaining rectangle vertices 
    rectNWLat   NUMBER;
    rectNWLon   NUMBER;
    rectSELat   NUMBER;
    rectSELon   NUMBER;

    rectHeight  NUMBER;
    rectWIdth   NUMBER;

    circleDistanceLat   NUMBER;
    circleDistanceLon   NUMBER;
    cornerDistanceSQ    NUMBER;

BEGIN
    -- Initialization of remaining rectangle vertices  
    rectNWLat := rectNELat;
    rectNWLon := rectSWLon;
    rectSELat := rectSWLat;
    rectSELon := rectNELon;

    -- Rectangle sides length calculation
    rectHeight := calc_distance(rectSWLat, rectSWLon, rectNWLat, rectNWLon);
    rectWidth := calc_distance(rectSWLat, rectSWLon, rectSELat, rectSELon);

    circleDistanceLat := abs( (circleCenterLat * kmToDegreeConst) - ((rectSWLat * kmToDegreeConst) + (rectHeight/2)) );
    circleDistanceLon := abs( (circleCenterLon * kmToDegreeConst) - ((rectSWLon * kmToDegreeConst) + (rectWidth/2)) );

    IF circleDistanceLon > ((rectWidth/2) + circleRadius) THEN
        RETURN -1;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLat > ((rectHeight/2) + circleRadius) THEN
        RETURN -1;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLon <= (rectWidth/2) THEN
        RETURN 0;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    IF circleDistanceLat <= (rectHeight/2) THEN
        RETURN 0;   --  -1 => NO Collision ; 0 => Collision Detected
    END IF;


    cornerDistanceSQ := POWER(circleDistanceLon - (rectWidth/2), 2) + POWER(circleDistanceLat - (rectHeight/2), 2);

    IF cornerDistanceSQ <=  POWER(circleRadius, 2) THEN
        RETURN 0;  --  -1 => NO Collision ; 0 => Collision Detected
    ELSE
        RETURN -1;  --  -1 => NO Collision ; 0 => Collision Detected
    END IF;

    RETURN -1;  --  -1 => NO Collision ; 0 => Collision Detected
END;    

Eulogia

Answer 21

def colision(rect, circle):
dx = rect.x - circle.x
dy = rect.y - circle.y
distance = (dy**2 + dx**2)**0.5
angle_to = (rect.angle + math.atan2(dx, dy)/3.1415*180.0) % 360
if((angle_to>135 and angle_to<225) or (angle_to>0 and angle_to<45) or (angle_to>315 and angle_to<360)):
    if distance <= circle.rad/2.+((rect.height/2.0)*(1.+0.5*abs(math.sin(angle_to*math.pi/180.)))):
        return True
else:
    if distance <= circle.rad/2.+((rect.width/2.0)*(1.+0.5*abs(math.cos(angle_to*math.pi/180.)))):
        return True
return False

Housewifely

Answer 22

I developed this algorithm while making this game: https://mshwf.github.io/mates/

If the circle touches the square, then the distance between the centerline of the circle and the centerline of the square should equal (diameter+side)/2. So, let's have a variable named touching that holds that distance. The problem was: which centerline should I consider: the horizontal or the vertical? Consider this frame:

Each centerline gives different distances, and only one is a correct indication to a no-collision, but using our human intuition is a start to understand how the natural algorithm works.

They are not touching, which means that the distance between the two centerlines should be greater than touching, which means that the natural algorithm picks the horizontal centerlines (the vertical centerlines says there's a collision!). By noticing multiple circles, you can tell: if the circle intersects with the vertical extension of the square, then we pick the vertical distance (between the horizontal centerlines), and if the circle intersects with the horizontal extension, we pick the horizontal distance:

Another example, circle number 4: it intersects with the horizontal extension of the square, then we consider the horizontal distance which is equal to touching.

Ok, the tough part is demystified, now we know how the algorithm will work, but how we know with which extension the circle intersects? It's easy actually: we calculate the distance between the most right x and the most left x (of both the circle and the square), and the same for the y-axis, the one with greater value is the axis with the extension that intersects with the circle (if it's greater than diameter+side then the circle is outside the two square extensions, like circle #7). The code looks like:

right = Math.max(square.x+square.side, circle.x+circle.rad);
left = Math.min(square.x, circle.x-circle.rad);

bottom = Math.max(square.y+square.side, circle.y+circle.rad);
top = Math.min(square.y, circle.y-circle.rad);

if (right - left > down - top) {
 //compare with horizontal distance
}
else {
 //compare with vertical distance
}

/*These equations assume that the reference point of the square is at its top left corner, and the reference point of the circle is at its center*/

Meraz

Answer 23

1. do a pre-check whether a circle fully encapsulating the rectangle collides with the circle.
2. check for rectangle corners within the circle.
3. For each edge, see if there is a line intersection with the circle. Project the center point C onto the line AB to get a point D. If the length of CD is less than radius, there was a collision.

    projectionScalar=dot(AC,AB)/(mag(AC)*mag(AB));
    if(projectionScalar>=0 && projectionScalar<=1) {
        D=A+AB*projectionScalar;
        CD=D-C;
        if(mag(CD)<circle.radius){
            // there was a collision
        }
    }

Harv

Answer 24

There is an incredibly simple way to do this, you have to clamp a point in x and y, but inside the square, while the center of the circle is between the two square border points in one of the perpendicular axis you need to clamp those coordinates to the parallel axis, just make sure the clamped coordinates do not exeed the limits of the square. Then just get the distance between the center of the circle and the clamped coordinates and check if the distance is less than the radius of the circle.

Here is how I did it (First 4 points are the square coordinates, the rest are circle points):

bool DoesCircleImpactBox(float x, float y, float x1, float y1, float xc, float yc, float radius){
    float ClampedX=0;
    float ClampedY=0;
    
    if(xc>=x and xc<=x1){
    ClampedX=xc;
    }
    
    if(yc>=y and yc<=y1){
    ClampedY=yc;
    }
    
    radius = radius+1;
    
    if(xc<x) ClampedX=x;
    if(xc>x1) ClampedX=x1-1;
    if(yc<y) ClampedY=y;
    if(yc>y1) ClampedY=y1-1;
    
    float XDif=ClampedX-xc;
    XDif=XDif*XDif;
    float YDif=ClampedY-yc;
    YDif=YDif*YDif;
    
    if(XDif+YDif<=radius*radius) return true;
    
    return false;
}

Bushbuck

Note that this answer is for AABB (Axis aligned Bounding Box), not for OBB (Oriented Bounding box). – Allonym

Answer 25

My method:

1. Calculate closest_point from the circle on/in OBB / rectangle (Closest point will lie on an edge/corner or inside)
2. Calculate squared_distance from the closest_point to the centre of the circle (Squared distance avoids a square root)
3. Return squared_distance <= circle radius squared

Aq

Answer 26

Using the answer below my Java version of circle - square collision/intersection detection:

public static boolean circleIntersectsSquare(Point circle, double radius,
        Point squareCenter, double halfSize) {
    double deltaX = Math.abs(circle.x - squareCenter.x);
    double deltaY = Math.abs(circle.y - squareCenter.y);

    if (deltaX >= (halfSize + radius)) return false;
    if (deltaY >= (halfSize + radius)) return false;

    if (deltaX < halfSize) return true;
    if (deltaY < halfSize) return true;

    double cornerDist = Math.pow(deltaX - halfSize, 2) +
        Math.pow(deltaY - halfSize, 2);

    return (cornerDist < radius*radius);
}

Original answer: Circle-Rectangle collision detection (intersection)

Jennine

Answer 27

Assuming you have the four edges of the rectangle check the distance from the edges to the center of the circle, if its less then the radius, then the shapes are intersecting.

if sqrt((rectangleRight.x - circleCenter.x)^2 +
        (rectangleBottom.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleRight.x - circleCenter.x)^2 +
        (rectangleTop.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleLeft.x - circleCenter.x)^2 +
        (rectangleTop.y - circleCenter.y)^2) < radius
// then they intersect

if sqrt((rectangleLeft.x - circleCenter.x)^2 +
        (rectangleBottom.y - circleCenter.y)^2) < radius
// then they intersect

Roughneck

What about the case where a small circle is entirely enclosed by a large rectangle? Surely that's an intersection, and would fail the test in this answer. – Duero

Ah yes, I didn't think of that. You could just add more checks like if sqrt( (rectangleRight.x/2 - circleCenter.x)^2 + (rectangleBottom.y/2 - circleCenter.y)^2) < radius then they intersect This will be long and slow, but off the top of my head thats the best I can come up with. – Roughneck

They can intersect on any [single one] point on any of the edges. You should find the edge-center distances as well. (Oh, and call your corners "corners" :) – Kellen

This appears to only detect when a corner is inside the circle. – Obstetrician