Group numeric vector by predefined maximal group sum

Question

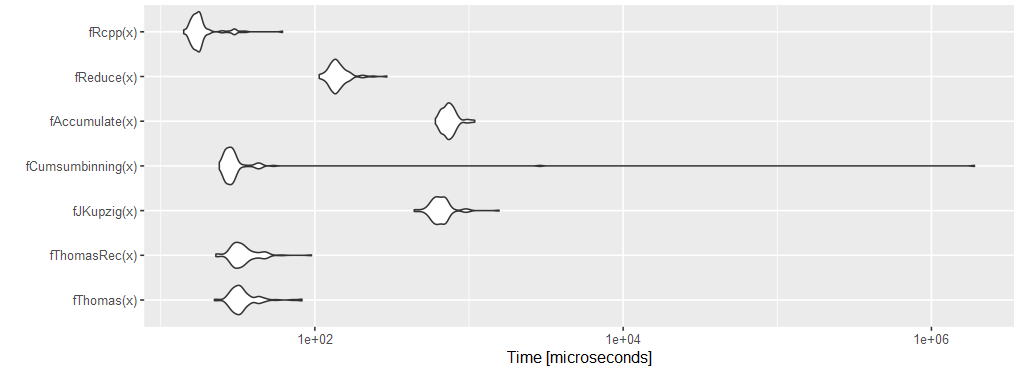
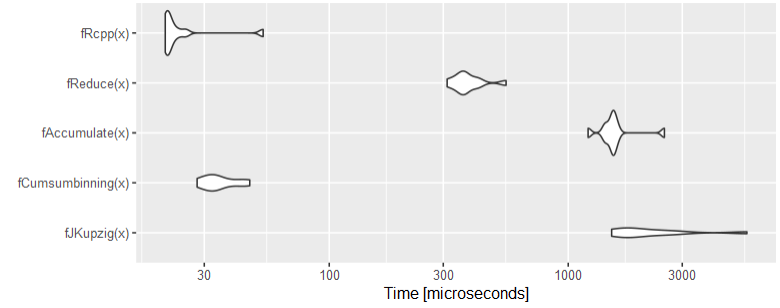
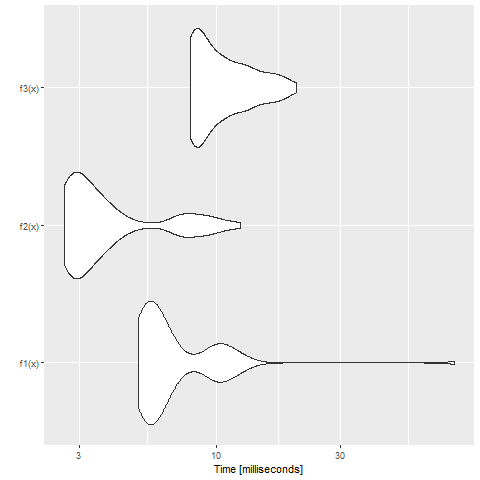
I have a numeric vector like this x <- c(1, 23, 7, 10, 9, 2, 4) and I want to group the elements from left to right with the constrain that each group sum must not exceed 25. Thus, here the first group is c(1, 23), the second is c(7, 10) and the last c(9, 2, 4). the expected output is a dataframe with a second column containing the groups:

data.frame(x= c(1, 23,  7,  10,  9,  2,  4), group= c(1, 1, 2, 2, 3, 3, 3))

I have tried different things with cumsum but am not able to kind of dynamically restart cumsum for the new group once the limit sum of 25 for the last group is reached.

Brune

Answer 1

Here is a solution using base R and cumsum (and lapply for iteration):

id <- c(seq(1, length(x),1)[!duplicated(cumsum(x) %/% 25)], length(x)+1)
id2 <- 1:length(id)
group <- unlist(lapply(1:(length(id)-1), function(x) rep(id2[x], diff(id)[x])))
data.frame(x=x, group=group)

   x group
1  1     1
2 23     1
3  7     2
4 10     2
5  9     3
6  2     3
7  4     3

Edit: New Approach using recursive function

Here is a new more efficient approach that should also cover the special case which @ЕгорШишунов considered and should work efficiently because it's written as a recursive function.

 recursiveFunction<- function(x, maxN=25, sumX=0, period=1, period2return=c()){
      sumX <- sumX + x[1]
      if (sumX >= maxN) { sumX=x[1]; period = period + 1}
      period2return <- c(period2return, period)
      if (length(x) == 1) { return(period2return)}
      return(recursiveFunction(x[-1], 25, sumX, period, period2return))
    }
    
    recursiveFunction(x, maxN=25)

Note that you should not change the entries for the last three function parameters (sumX=0, period=1, period2return=c()) because they are only important during the recursive call of the function.

Hammonds

Other questions are as good but that is the easiest to me to understand. Thanks – Brune

It is also wrong solution. For x = c(10, 20, 20, 20) it returns c(1, 2, 3, 3) but true answer is c(1, 2, 3, 4). base function cumsum is bad for this task cause it forgets about the rests. – Pyretotherapy

@ЕгорШишунов What do you mean with "it forgets about the rests"? – Brune

Let x = c(10, 20, 20, 20), cumsum(x) = c(10, 30, 50, 70). And last 2 elements have group 3 (cause 50 %/% 25 == 70 %/% 25 == 2). But if we solve problem by hand: sum of first and second elements is greater than 25 so they will be different groups (1 and 2). Sum of second and third element is greater than 25 so third element will be in group 3. And sum of last 2 elements is greater than 25 so the first element should be in group 4. We check sum of elements in last group (third element = 20) and new element (fourth element = 20) and 20 %/% 25 != 40 %/% 25 (we have not rest = 30). – Pyretotherapy

@ЕгорШишунов I think not cumsum is the problem but the (combination with) %/% because I get the correct solution for x = c(10, 20, 20, 20) with the answer from "ThomasIsCoding" which is using cumsum, too. – Brune

You are right, I think the problem is that I'm using cumsum without any loop, or e.g. like Mael suggested with accumulate (which is by the way a very nice and pure solution). – Hammonds

Loop and vectorized function? It's bad case. If you can write loop in R you can do it in Rcpp. But Rcpp is faster. – Pyretotherapy

Answer 2

I think cpp function is the fastest way:

library(Rcpp)
cppFunction(
    "IntegerVector GroupBySum(const NumericVector& x, const double& max_sum = 25)
    {
        double sum = 0;
        int cnt = 0;
        int period = 1;
        IntegerVector res(x.size());
        for (int i = 0; i < x.size(); ++i)
        {
            ++cnt;
            sum += x[i];
            if (sum > max_sum)
            {
                sum = x[i];
                if (cnt > 1)
                    ++period;
                cnt = 1;
            }
            res[i] = period;
        }
        return res;
    }"
)
GroupBySum(c(1, 23,  7,  10,  9,  2,  4), 25)

Selfappointed

Answer 3

You can use the cumsumbinning built-in function from the MESS package:

# install.packages("MESS")
MESS::cumsumbinning(x, 25, cutwhenpassed = F)
# [1] 1 1 2 2 3 3 3

Or it can be done with purrr::accumulate:

cumsum(x == accumulate(x, ~ifelse(.x + .y <= 25, .x + .y, .y)))
# [1] 1 1 2 2 3 3 3

output

group <- MESS::cumsumbinning(x, 25, cutwhenpassed = F)
data.frame(x= c(1, 23,  7,  10,  9,  2,  4), 
           group = group)

   x group
1  1     1
2 23     1
3  7     2
4 10     2
5  9     3
6  2     3
7  4     3

---

Quick benchmark:

x<- c(1, 23,  7,  10,  9,  2,  4)
bm <- microbenchmark(
  fThomas(x),
  fThomasRec(x),
  fJKupzig(x), 
  fCumsumbinning(x), 
  fAccumulate(x),
  fReduce(x),
  fRcpp(x),
  times = 100L,
  setup = gc(FALSE)
)
autoplot(bm)

Егор Шишунов's Rcpp is the fastest, closely followed by MESS::cumsumbinning and ThomasIsCoding's both functions.

With n = 100, the gap gets bigger but Rcpp and cumsumbinning are still the top choices and the while loop option is no longer efficient (I had to remove ThomasIsCoding's functions because the execution time was too long):

x = runif(100, 1, 50)

Loyola

your accumulate wont work eg x<- c(1, 19, 24, 10, 9, 2, 4) – Hedden

Edited. It should work now. – Flocculent

Can you set x = runif(100, 1, 50)?. If size x = 1e5 Rcpp is much better (and loop in R is very bad) I want to know what is the test time if size = 100. – Pyretotherapy

Done! Interesting results! – Flocculent

Could you add also the recursiveFunction to your results? I would be very interested to see the benchmark. – Hammonds

Added. For larger vector (runif(100, 1, 50)), I reach the stack size limit. – Flocculent

Answer 4

We can try this as a programming practice if you like :)

f1 <- function(x) {
  group <- c()
  while (length(x)) {
    idx <- cumsum(x) <= 25
    x <- x[!idx]
    group <- c(group, rep(max(group, 0) + 1, sum(idx)))
  }
  group
}

or

f2 <- function(x) {
  group <- c()
  g <- 0
  while (length(x)) {
    cnt <- s <- 0
    for (i in seq_along(x)) {
      s <- s + x[i]
      if (s <= 25) {
        cnt <- cnt + 1
      } else {
        break
      }
    }
    g <- g + 1
    group <- c(group, rep(g, cnt))
    x <- x[-(1:cnt)]
  }
  group
}

or

f3 <- function(x) {
  s <- cumsum(x)
  r <- c()
  grp <- 1
  while (length(s)) {
    idx <- (s <= 25)
    r <- c(r, rep(grp, sum(idx)))
    grp <- grp + 1
    s <- s[!idx] - tail(s[idx], 1)
  }
  r
}

which gives

[1] 1 1 2 2 3 3 3

and benchmarking among them looks like

set.seed(1)
set.seed(1)
x <- runif(1e3, 0, 25)
bm <- microbenchmark(
  f1(x),
  f2(x),
  f3(x),
  check = "equivalent"
)
autoplot(bm)

---

Recursion version

Another option is using recursion (based on f1())

f <- function(x, res = c()) {
  if (!length(x)) {
    return(res)
  }
  idx <- cumsum(x) <= 25
  Recall(x[!idx], res = c(res, list(x[idx])))
}

and you will see

> f(x)
[[1]]
[1]  1 23

[[2]]
[1]  7 10

[[3]]
[1] 9 2 4

Viable

Answer 5

In base R you could also use Reduce:

do.call(rbind, Reduce(\(x,y) if((z<-x[1] + y) > 25) c(y, x[2]+1)
       else c(z, x[2]), x[-1], init = c(x[1], 1), accumulate = TRUE))

     [,1] [,2]
[1,]    1    1
[2,]   24    1
[3,]    7    2
[4,]   17    2
[5,]    9    3
[6,]   11    3
[7,]   15    3

Breaking it down:

f <- function(x, y){
  z <- x[1] + y
  if(z > 25) c(y, x[2] + 1)
  else c(z, x[2])
}

do.call(rbind, Reduce(f, x[-1], init = c(x[1], 1), accumulate = TRUE))

if using accumulate

library(tidyverse)
accumulate(x[-1], f, .init = c(x[1], 1)) %>%
invoke(rbind, .)

     [,1] [,2]
[1,]    1    1
[2,]   24    1
[3,]    7    2
[4,]   17    2
[5,]    9    3
[6,]   11    3
[7,]   15    3

Hedden