Update
Here we made some improvement on the previous answer, where the result is stored in matrix (instead of list), and arrangement::permuations is applied (instead of pracma::perms (thank recommendation from @Gregor Thomas)
f_TIC2 <- function(x) {
u <- unique(x)
idx <- match(x, u)
n <- max(idx)
m <- matrix(u[perms(1:n)], ncol = n)
matrix(t(m)[c(outer(idx, (0:(nrow(m) - 1)) * ncol(m), `+`))], nrow = nrow(m), byrow = TRUE)
}
f_TIC2Arr <- function(x) {
u <- unique(x)
idx <- match(x, u)
n <- max(idx)
m <- matrix(u[permutations(1:n)], ncol = n)
matrix(t(m)[c(outer(idx, (0:(nrow(m) - 1)) * ncol(m), `+`))], nrow = nrow(m), byrow = TRUE)
}
and the output looks like
> f_TIC2(c("a", "b", "b", "c", "b"))
[,1] [,2] [,3] [,4] [,5]
[1,] "c" "b" "b" "a" "b"
[2,] "c" "a" "a" "b" "a"
[3,] "b" "c" "c" "a" "c"
[4,] "b" "a" "a" "c" "a"
[5,] "a" "b" "b" "c" "b"
[6,] "a" "c" "c" "b" "c"
> f_TIC2Arr(c("a", "b", "b", "c", "b"))
[,1] [,2] [,3] [,4] [,5]
[1,] "a" "b" "b" "c" "b"
[2,] "a" "c" "c" "b" "c"
[3,] "b" "a" "a" "c" "a"
[4,] "b" "c" "c" "a" "c"
[5,] "c" "a" "a" "b" "a"
[6,] "c" "b" "b" "a" "b"
Benchmarking
Here is a benchmark among some of the existing answers (Maël's solution is computational heavy, thus being skipped.)
NB: This benchmark is NOT 100% fair since my improved solutions yield matrices rather than lists, which save a lot of time. Thus, the comparsion is not saying mine is the fastest but indicating the possible approaches to improve the performance.
library(RcppAlgos)
library(arrangements)
library(pracma)
f_TIC1 <- function(x) {
idx <- match(x, unique(x))
m <- asplit(matrix(unique(x)[perms(1:max(idx))], ncol = max(idx)), 1)
Map(`[`, m, list(idx))
}
f_TIC1Arr <- function(x) {
idx <- match(x, unique(x))
m <- asplit(matrix(unique(x)[permutations(1:max(idx))], ncol = max(idx)), 1)
Map(`[`, m, list(idx))
}
f_TIC2 <- function(x) {
u <- unique(x)
idx <- match(x, u)
n <- max(idx)
m <- matrix(u[perms(1:n)], ncol = n)
matrix(t(m)[outer(idx, (0:(nrow(m) - 1)) * ncol(m), `+`)], nrow = nrow(m), byrow = TRUE)
}
f_TIC2Arr <- function(x) {
u <- unique(x)
idx <- match(x, u)
n <- max(idx)
m <- matrix(u[permutations(1:n)], ncol = n)
matrix(t(m)[outer(idx, (0:(nrow(m) - 1)) * ncol(m), `+`)], nrow = nrow(m), byrow = TRUE)
}
f_GT <- function(x) {
ux <- unique(x)
xi <- as.integer(factor(x))
perm <- permutations(seq_along(ux))
apply(perm, MARGIN = 1, FUN = \(p) ux[p][xi], simplify = FALSE)
}
f_RS <- function(x) {
permuteGeneral(uv <- unique(x), length(uv), FUN = \(m) uv[match(x, m)])
}
set.seed(1)
x <- sample(letters[1:10], 10, replace = TRUE)
bm <- bench::mark(
f_GT = f_GT(x),
f_TIC1 = f_TIC1(x),
f_TIC1Arr = f_TIC1Arr(x),
f_TIC2 = f_TIC2(x),
f_TIC2Arr = f_TIC2Arr(x),
f_RS = f_RS(x),
check = FALSE
)
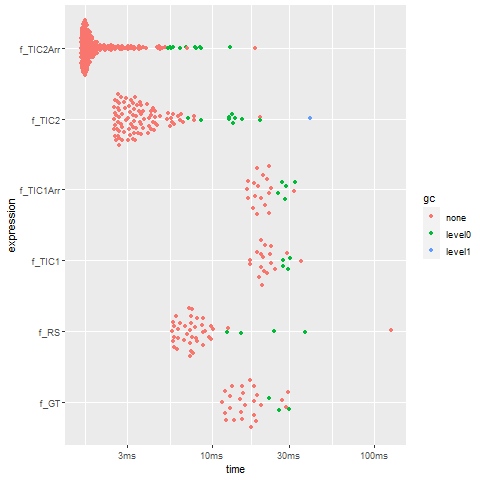
autoplot(bm)
and you will see
> bm
# A tibble: 6 x 13
expression min median `itr/sec` mem_alloc `gc/sec` n_itr n_gc total_time
<bch:expr> <bch:t> <bch:t> <dbl> <bch:byt> <dbl> <int> <dbl> <bch:tm>
1 f_GT 11.55ms 15.57ms 58.9 315.14KB 7.06 25 3 425ms
2 f_TIC1 17.05ms 20.8ms 45.5 2.58MB 10.1 18 4 396ms
3 f_TIC1Arr 16.45ms 19.62ms 48.9 1.06MB 13.6 18 5 368ms
4 f_TIC2 2.47ms 3.31ms 259. 3.84MB 28.5 91 10 351ms
5 f_TIC2Arr 1.54ms 1.7ms 469. 2.35MB 26.2 197 11 420ms
6 f_RS 5.66ms 7.46ms 93.9 72.75KB 9.63 39 4 415ms
# ... with 4 more variables: result <list>, memory <list>, time <list>,
# gc <list>
and
![enter image description here]()
Previous Answer
You can try pracma::perms like below
library(pracma)
f <- function(x) {
idx <- match(x, unique(x))
m <- asplit(matrix(unique(x)[perms(1:max(idx))], ncol = max(idx)), 1)
Map(`[`, m, list(idx))
}
and you will see
> f(c("a", "a", "a", "b", "b", "b", "a", "a", "b", "b"))
[[1]]
[1] "b" "b" "b" "a" "a" "a" "b" "b" "a" "a"
[[2]]
[1] "a" "a" "a" "b" "b" "b" "a" "a" "b" "b"
> f(c("a", "b", "b", "c", "b"))
[[1]]
[1] "c" "b" "b" "a" "b"
[[2]]
[1] "c" "a" "a" "b" "a"
[[3]]
[1] "b" "c" "c" "a" "c"
[[4]]
[1] "b" "a" "a" "c" "a"
[[5]]
[1] "a" "b" "b" "c" "b"
[[6]]
[1] "a" "c" "c" "b" "c"