Sierpinski's Triangle Pygame Recursive

So for my current university paper we are meant to create a Sierpinksi Triangle and Recursively draw new triangles inside.

The original code we got was this:

import sys, pygame

# a function that will draw a right-angled triangle of a given size anchored at a given location
def draw_triangle(screen, x, y, size):
        pygame.draw.polygon(screen,white,[[x,y], [x+size,y], [x,y-size]])

############################################################################################# 
# Define a function that will draw Sierpinski's Triangle at a given size anchored at a given location
# You need to update this function 
# currently only one triangle is drawn

def sierpinski(screen, x, y, size):
        draw_triangle(screen, x, y, size)

############################################################################################# 

# Initialize the game engine
pygame.init()

# Define the colors we will use in RGB format
black = [ 0, 0, 0]
white = [255,255,255]
blue = [ 0, 0,255]
green = [ 0,255, 0]
red = [255, 0, 0]

# Set the height and width of the screen
size=[512, 512]
screen=pygame.display.set_mode(size)

# Loop until the user clicks the close button.
done=False
clock = pygame.time.Clock()


while done==False:

    # This limits the while loop to a max of 10 times per second.
    # Leave this out and we will use all CPU we can.
    clock.tick(10)

    for event in pygame.event.get(): # User did something
        if event.type == pygame.QUIT: # If user clicked close
            done=True # Flag that we are done so we exit this loop

    # Clear the screen and set the screen background
    screen.fill(black)

    # Draw Sierpinski's triangle at a given size anchored at a given location

    sierpinski(screen,0, 512, 512)

    # Go ahead and update the screen with what we've drawn.
    # This MUST happen after all the other drawing commands.
    pygame.display.flip()

# Tidy up
pygame.quit ()

Ok I know that this only creates a single triangle. Here is what I did to make it work "sort of":

I created a new triangle function to draw a upside down triangle:

def draw_upside_down_triangle(screen, x, y, size, color):
        pygame.draw.polygon(screen, color, [[x+size, y+size], [x+size, y], [x, y]])

Then I updated the old triangle function to accept a color variable:

def draw_triangle(screen, x, y, size, color):
        pygame.draw.polygon(screen, color, [[x, y], [x+size, y], [x, y-size]])

After that I updated the main function which will recursively draw triangles:

def sierpinski(screen, x, y, size):
    if size < 10:
        return False
    else:
        draw_triangle(screen, x, y, size, white)
        draw_upside_down_triangle(screen, x, y/2, size/2, black)
        sierpinski(screen, x+size/2, y+size/2, size/2)
        sierpinski(screen, x, y-size/2, size/2)
        sierpinski(screen, x, y, size/2)
        sierpinski(screen, x, y+size/2, size/2)

I started the function off

By adding the exit argument (when the triangle get's too small return false)
If it's not too small then draw the first triangle in white
After that draw an upside down triangle half the size at the same x location but half the y location in black (this creates the 3 triangle illusion)
After all of that I have 4 recursive calls, based on experimentation I know that the order of these calls matter as the output changes radically when changed.

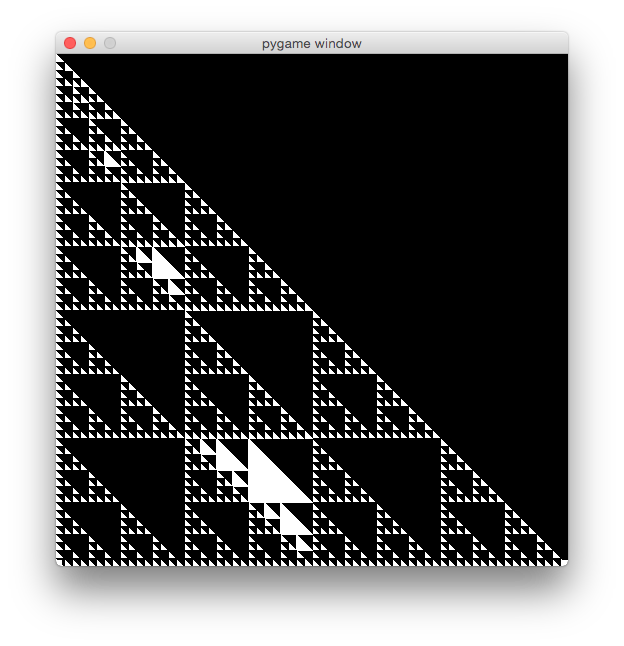
At the moment the current output is as follows:

I am not asking for anyone to finish or correct my code simply a better understanding or a point in the right direction. Have been battling with this one for a few hours.

Thanks!

Take a look at the following link that implements Sierpinski's triangle...

http://interactivepython.org/runestone/static/pythonds/Recursion/graphical.html#sierpinski-triangle

Lots of good discussion around the problem and 40 some lines of code to implement it.

Also because of the way the turtle module works you can watch each triangle get draw one by one. This is extremely helpful as you review the code because you can visualize the levels of recursion and when they happen. I don't know how hard this would be to implement in pygame but if you can slow down the triangle creation it makes understanding the logic that much easier.

You say you need the 4 recursive calls based on experiment but can you explain the logic behind it? Intuitively this seems wrong as you only need three new triangles plus one partially covered parent to equal four smaller equilateral triangles. (See how this is done in the link?)

Can you explain why you are using an upside down triangle method? This seems sort of like a bug-prone work around? You should be able to draw the upside down triangles using negative space from your normal triangle function. In the link you'll see that the author draws a green triangle facing the same direction as everything else but later covers it up with more triangles until the green one is facing the opposite direction.

All in all it looks like you're close. You just need to get that last piece of recursion logic right.

P.S.

One minor minor style critique - only because this is written in python and readability counts. You can use While True and then break to avoid the extra variable done.

Recommended topics

Hot tags