Optimization and speedup of a mathematical function in python

Question

The purpose of this mathematical function is to compute a distance between two (or more) protein structures using dihedral angles:

It is very useful in structural biology, for example. And I already code this function in python using numpy, but the goal is to have a faster implementation. As computation time reference, I use the euclidean distance function available in the scikit-learn package.

Here the code I have for the moment:

import numpy as np
import numexpr as ne
from sklearn.metrics.pairwise import euclidean_distances

# We have 10000 structures with 100 dihedral angles
n = 10000
m = 100

# Generate some random data
c = np.random.rand(n,m)
# Generate random int number
x = np.random.randint(c.shape[0])

print c.shape, x

# First version with numpy of the dihedral_distances function
def dihedral_distances(a, b):
    l = 1./a.shape[0]
    return np.sqrt(l* np.sum((0.5)*(1. - np.cos(a-b)), axis=1))

# Accelerated version with numexpr
def dihedral_distances_ne(a, b):
    l = 1./a.shape[0]
    tmp = ne.evaluate('sum((0.5)*(1. - cos(a-b)), axis=1)')
    return ne.evaluate('sqrt(l* tmp)')

# The function of reference I try to be close as possible 
# in term of computation time
%timeit euclidean_distances(c[x,:], c)[0]
1000 loops, best of 3: 1.07 ms per loop

# Computation time of the first version of the dihedral_distances function
# We choose randomly 1 structure among the 10000 structures.
# And we compute the dihedral distance between this one and the others
%timeit dihedral_distances(c[x,:], c)
10 loops, best of 3: 21.5 ms per loop

# Computation time of the accelerated function with numexpr
%timeit dihedral_distances_ne(c[x,:], c)
100 loops, best of 3: 9.44 ms per loop

9.44 ms it's very fast, but it's very slow if you need to run it a million times. Now the question is, how to do that? What is the next step? Cython? PyOpenCL? I have some experience with PyOpenCL, however I never code something as elaborate as this one. I don't know if it's possible to compute the dihedral distances in one step on GPU as I do with numpy and how to proceed.

Thank you for helping me!

EDIT: Thank you guys! I am currently working on the full solution and once it's finished I will put the code here.

CYTHON VERSION:

%load_ext cython
import numpy as np

np.random.seed(1234)

n = 10000
m = 100

c = np.random.rand(n,m)
x = np.random.randint(c.shape[0])

print c.shape, x

%%cython --compile-args=-fopenmp --link-args=-fopenmp --force

import numpy as np
cimport numpy as np
from libc.math cimport sqrt, cos
cimport cython
from cython.parallel cimport parallel, prange

# Define a function pointer to a metric
ctypedef double (*metric)(double[: ,::1], np.intp_t, np.intp_t)

cdef extern from "math.h" nogil:
    double cos(double x)
    double sqrt(double x)

@cython.boundscheck(False)
@cython.wraparound(False)
@cython.cdivision(True)
cdef double dihedral_distances(double[:, ::1] a, np.intp_t i1, np.intp_t i2):
    cdef double res
    cdef int m
    cdef int j

    res = 0.
    m = a.shape[1]

    for j in range(m):
        res += 1. - cos(a[i1, j] - a[i2, j])

    res /= 2.*m

    return sqrt(res)

@cython.boundscheck(False)
@cython.wraparound(False)
@cython.cdivision(True)
cdef double dihedral_distances_p(double[:, ::1] a, np.intp_t i1, np.intp_t i2):
    cdef double res
    cdef int m
    cdef int j

    res = 0.
    m = a.shape[1]

    with nogil, parallel(num_threads=2):
        for j in prange(m, schedule='dynamic'):
            res += 1. - cos(a[i1, j] - a[i2, j])

    res /= 2.*m

    return sqrt(res)

@cython.boundscheck(False)
@cython.wraparound(False)
def pairwise(double[: ,::1] c not None, np.intp_t x, p = True):
    cdef metric dist_func
    if p:
        dist_func = &dihedral_distances_p
    else:
        dist_func = &dihedral_distances

    cdef np.intp_t i, n_structures
    n_samples = c.shape[0]

    cdef double[::1] res = np.empty(n_samples)

    for i in range(n_samples):
        res[i] = dist_func(c, x, i)

    return res

%timeit pairwise(c, x, False)
100 loops, best of 3: 17 ms per loop    

# Parallel version
%timeit pairwise(c, x, True)
10 loops, best of 3: 37.1 ms per loop

So I follow your link to create the cython version of the dihedral distances function. We gain some speed, not so much, but it is still slower than the numexpr version (17ms vs 9.44ms). So I tried to parallelize the function using prange and it is worse (37.1ms vs 17ms vs 9.4ms)!

Do I miss something?

Gabi

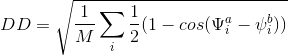
A couple of small improvements are: 1) put the *0.5 outside of the sum; and, 2) sum the cos before subtracting the from 1 (which will be more accurate as well, since the sum will hang around 1). For me these bring it from 25ms to 17ms. I know you're looking for more, but this is what I got and thought it might help a bit. – Antediluvian

Trying out cython is easy and can give quite a speedup (YMMV, of course): jakevdp.github.io/blog/2012/08/08/memoryview-benchmarks – Schumann

@Antediluvian Effectively with 1) I gain more than 1ms but 2) give me an error RuntimeWarning: invalid value encountered in sqrt. – Gabi

For 2, if you sum over N items then sqrt(sum(1 - cos(x))) becomes sqrt(N - sum(cos(x))). Did you remember the N? – Antediluvian

@Antediluvian Yeah, you're right! I hadn't seen the trick. Thank you! – Gabi

Answer 1

If you're willing to use http://pythran.readthedocs.io/, you can leverage on the numpy implementation and get better performance than cython for that case:

#pythran export np_cos_norm(float[], float[])
import numpy as np
def np_cos_norm(a, b):
    val = np.sum(1. - np.cos(a-b))
    return np.sqrt(val / 2. / a.shape[0])

And compile it with:

pythran fast.py

To get an average x2 over the cython version.

If using:

pythran fast.py -march=native -DUSE_BOOST_SIMD -fopenmp

You'll get a vectorized, parallel version that runs slightly faster:

100000 loops, best of 3: 2.54 µs per loop
1000000 loops, best of 3: 674 ns per loop

100000 loops, best of 3: 16.9 µs per loop
100000 loops, best of 3: 4.31 µs per loop

10000 loops, best of 3: 176 µs per loop
10000 loops, best of 3: 42.9 µs per loop

(using the same testbed as ev-br)

Zerelda

Cocorico! \o/ It seems very promising but not so easy too use (pastebin). Apparently I have a problem with the boost library or something else. It doesn't compile. Other detail I didn't mention in the pastebin, I am running under OSX 10.9.5. – Gabi

@NoExiT: What if you add -DNDEBUG to the compile flags, as in pythran -DNDEBUG fast.py ? – Zerelda

What if you force g++-4.9 as a compiler? – Zerelda

We are close to the end! 1) So I installed g++-4.9 using homebrew and this link, then 2) I modify .pythranrc with cxx = g++-4.9 and finally when I ran it again I only had one error ld: library not found for -lboost_python-mt. I put the complete report here. – Gabi

Update: I didn't install boost-python ... So I brew install boost-python. Then I had this error ld: library not found for -ltcmalloc_minimal. So I updated the .pythranrc file to ldflags = -fPIC only. And now it's working! \o/ (installation summary) – Gabi

you forgot the -DNDEBUG again :-) – Zerelda

Yes, I did it on purpose to try if it works without ... and the answer is no. Whatever, when I do pythran -DNDEBUG fast.py; python -c 'import fast' I obtain a segmentation fault Segmentation fault: 11. So, there is still have a problem. – Gabi

Let us continue this discussion in chat. – Zerelda

@serge-sans-paille: can you provide an explanation of how pythran might provide a speed improvement? For this simple equation, there's very little looping and almost all of the time will be spent in numpy's compiled C code. That is, in the absence of Python loops, I don't see why compiling python code will give a speed improvement over per-compiled numpy code. Is it just a better compiler? – Antediluvian

@tom10: numpy creates a temporary array for each operation. So to compute np.sum(1. - np.cos(a-b)) it uses 3 temporary (and useless) arrays. Pythran fuses the loops, which also makes vectorization and parallelization more efficient. – Zerelda

Answer 2

Here's a quick-and-dirty try with cython, for just a pair of 1D arrays:

(in an IPython notebook)

%%cython

cimport cython
cimport numpy as np

cdef extern from "math.h":
    double cos(double x) nogil
    double sqrt(double x) nogil

def cos_norm(a, b):
    return cos_norm_impl(a, b)

@cython.boundscheck(False)
@cython.wraparound(False)
@cython.cdivision(True)
cdef double cos_norm_impl(double[::1] a, double[::1] b) nogil:
    cdef double res = 0., val
    cdef int m = a.shape[0]
    # XXX: shape of b not checked
    cdef int j

    for j in range(m):
        val = a[j] - b[j]
        res += 1. - cos(val)
    res /= 2.*m

    return sqrt(res)

Comparing with a straightforward numpy implementation,

def np_cos_norm(a, b):
    val = np.add.reduce(1. - np.cos(a-b))
    return np.sqrt(val / 2. / a.shape[0])

I get

np.random.seed(1234)

for n in [100, 1000, 10000]:
    x = np.random.random(n)
    y = np.random.random(n)
    %timeit cos_norm(x, y)
    %timeit np_cos_norm(x, y)
    print '\n'

100000 loops, best of 3: 3.04 µs per loop
100000 loops, best of 3: 12.4 µs per loop

100000 loops, best of 3: 18.8 µs per loop
10000 loops, best of 3: 30.8 µs per loop

1000 loops, best of 3: 196 µs per loop
1000 loops, best of 3: 223 µs per loop

So, depending on the dimensionality of your vectors, you can get from a factor of 4 to nil of a speedup.

For computing pairwise distances, you can probably do much better, as shown in this blog post, but of course YMMV.

Schumann

Thank you @ev-br! I am working on it. There is just a little error in the np_cos_norm function, it's val = np.add.reduce(1. - np.cos(a-b), axis=1). – Gabi

This is deliberate: I only handle 1D arrays here. – Schumann