Stochastic gradient descent from gradient descent implementation in R

Question

I have a working implementation of multivariable linear regression using gradient descent in R. I'd like to see if I can use what I have to run a stochastic gradient descent. I'm not sure if this is really inefficient or not. For example, for each value of α I want to perform 500 SGD iterations and be able to specify the number of randomly picked samples in each iteration. It would be nice to do this so I could see how the number of samples influences the results. I'm having trouble through with the mini-batching and I want to be able to easily plot the results.

This is what I have so far:

 # Read and process the datasets

# download the files from GitHub
download.file("https://raw.githubusercontent.com/dbouquin/IS_605/master/sgd_ex_data/ex3x.dat", "ex3x.dat", method="curl")
x <- read.table('ex3x.dat')

# we can standardize the x vaules using scale()
x <- scale(x)

download.file("https://raw.githubusercontent.com/dbouquin/IS_605/master/sgd_ex_data/ex3y.dat", "ex3y.dat", method="curl")
y <- read.table('ex3y.dat')

# combine the datasets
data3 <- cbind(x,y)
colnames(data3) <- c("area_sqft", "bedrooms","price")
str(data3)

head(data3)

################ Regular Gradient Descent
# http://www.r-bloggers.com/linear-regression-by-gradient-descent/

# vector populated with 1s for the intercept coefficient
x1 <- rep(1, length(data3$area_sqft))

# appends to dfs
# create x-matrix of independent variables
x <- as.matrix(cbind(x1,x))
# create y-matrix of dependent variables
y <- as.matrix(y)
L <- length(y)

# cost gradient function: independent variables and values of thetas
cost <- function(x,y,theta){
  gradient <- (1/L)* (t(x) %*% ((x%*%t(theta)) - y))
  return(t(gradient)) 
}

# GD simultaneous update algorithm
# https://www.coursera.org/learn/machine-learning/lecture/8SpIM/gradient-descent
GD <- function(x, alpha){
      theta <- matrix(c(0,0,0), nrow=1) 
  for (i in 1:500) {
       theta <- theta - alpha*cost(x,y,theta)  
       theta_r <- rbind(theta_r,theta)    
  }
return(theta_r)
}

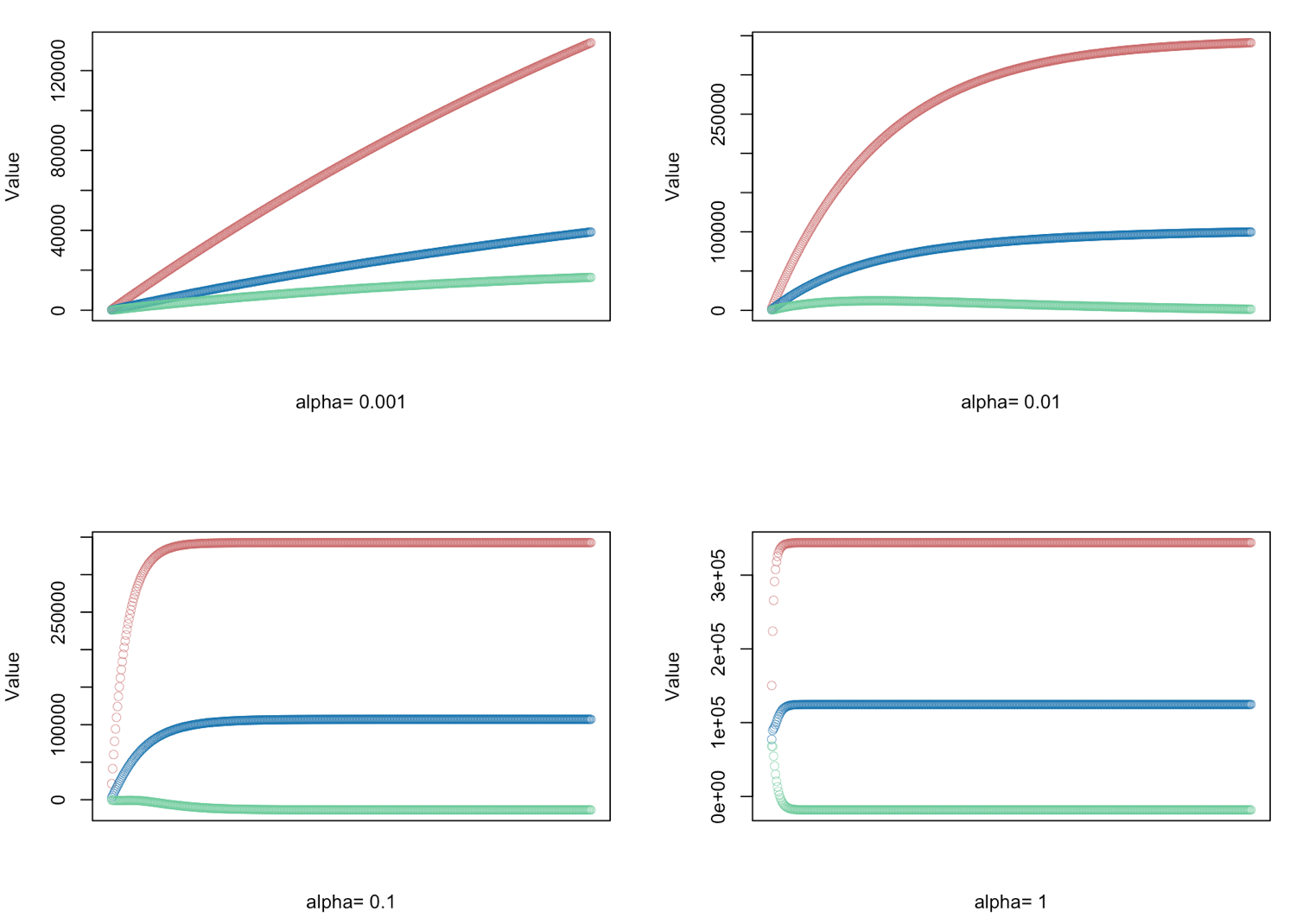
# gradient descent α = (0.001, 0.01, 0.1, 1.0) - defined for 500 iterations

alphas <- c(0.001,0.01,0.1,1.0)

# Plot price, area in square feet, and the number of bedrooms

# create empty vector theta_r
theta_r<-c()

for(i in 1:length(alphas)) {

 result <- GD(x, alphas[i])

 # red = price 
 # blue = sq ft 
 # green = bedrooms
 plot(result[,1],ylim=c(min(result),max(result)),col="#CC6666",ylab="Value",lwd=0.35,
      xlab=paste("alpha=", alphas[i]),xaxt="n") #suppress auto x-axis title
      lines(result[,2],type="b",col="#0072B2",lwd=0.35)
      lines(result[,3],type="b",col="#66CC99",lwd=0.35)
}

Is it more practical to find a way to use sgd()? I can't seem to figure out how to have the level of control I'm looking for with the sgd package

Valeryvalerye

sgd has two arguments, model.control and sgd.control both of which have a pretty big list of options you can pass. do you want more control than that? what else are you trying to do? – Splitlevel

Maybe I'm just not understanding how to set the number of samples. Do you know of a good example using multivariable linear regression with sgd? – Valeryvalerye

I don't see that option. you can always do it yourself, ie, sample 500 of your total and use the subset of data in your models. remember to set.seed – Splitlevel

I'll give it a shot, I'm just having so much trouble with the sgd documentation. That's why it would be nice to build on what I have if possible. Have you seen any walk-throughs or examples using sgd for multivariable linear regression in R? I find linear regression only. – Valeryvalerye

For example, I've found this post, but it's not very helpful. – Valeryvalerye

?sgd has a multivariable linear example although it is quite simple. there is also the vignette – Splitlevel

hmm... hadn't seen this paper yet. I'll have to read it today--thanks! – Geomancer

Checking the source code, model.control and sgd.control appear to be controlled by sgd:::valid_model_control and sgd:::valid_sgd_control, although I don't see options for the number of observations. Given that sgd is guaranteed to be optimal with batch size == 1, there may not be an option. Typically batch size is only specified to control the learning time (in computation time, not number of iterations)... Since the package is under active development, I suggest you raise an issue with the authors... even if you use rawr's wrapper below – Geomancer

Answer 1

Sticking with what you have now

## all of this is the same

download.file("https://raw.githubusercontent.com/dbouquin/IS_605/master/sgd_ex_data/ex3x.dat", "ex3x.dat", method="curl")
x <- read.table('ex3x.dat')
x <- scale(x)
download.file("https://raw.githubusercontent.com/dbouquin/IS_605/master/sgd_ex_data/ex3y.dat", "ex3y.dat", method="curl")
y <- read.table('ex3y.dat')
data3 <- cbind(x,y)
colnames(data3) <- c("area_sqft", "bedrooms","price")
x1 <- rep(1, length(data3$area_sqft))
x <- as.matrix(cbind(x1,x))
y <- as.matrix(y)
L <- length(y)
cost <- function(x,y,theta){
  gradient <- (1/L)* (t(x) %*% ((x%*%t(theta)) - y))
  return(t(gradient)) 
}

I added y to your GD function and created a wrapper function, myGoD, to call yours but first subsetting the data

GD <- function(x, y, alpha){
  theta <- matrix(c(0,0,0), nrow=1)
  theta_r <- NULL
  for (i in 1:500) {
    theta <- theta - alpha*cost(x,y,theta)  
    theta_r <- rbind(theta_r,theta)    
  }
  return(theta_r)
}

myGoD <- function(x, y, alpha, n = nrow(x)) {
  idx <- sample(nrow(x), n)
  y <- y[idx, , drop = FALSE]
  x <- x[idx, , drop = FALSE]
  GD(x, y, alpha)
}

Check to make sure it works and try with different Ns

all.equal(GD(x, y, 0.001), myGoD(x, y, 0.001))
# [1] TRUE

set.seed(1)
head(myGoD(x, y, 0.001, n = 20), 2)
#          x1        V1       V2
# V1 147.5978  82.54083 29.26000
# V1 295.1282 165.00924 58.48424

set.seed(1)
head(myGoD(x, y, 0.001, n = 40), 2)
#          x1        V1        V2
# V1 290.6041  95.30257  59.66994
# V1 580.9537 190.49142 119.23446

Here is how you can use it

alphas <- c(0.001,0.01,0.1,1.0)
ns <- c(47, 40, 30, 20, 10)

par(mfrow = n2mfrow(length(alphas)))
for(i in 1:length(alphas)) {

  # result <- myGoD(x, y, alphas[i]) ## original
  result <- myGoD(x, y, alphas[i], ns[i])

  # red = price 
  # blue = sq ft 
  # green = bedrooms
  plot(result[,1],ylim=c(min(result),max(result)),col="#CC6666",ylab="Value",lwd=0.35,
       xlab=paste("alpha=", alphas[i]),xaxt="n") #suppress auto x-axis title
  lines(result[,2],type="b",col="#0072B2",lwd=0.35)
  lines(result[,3],type="b",col="#66CC99",lwd=0.35)
}

You don't need the wrapper function--you can just change your GD slightly. It is always good practice to explicitly pass arguments to your functions rather than relying on scoping. Before you were assuming that y would be pulled from your global environment; here y must be given or you will get an error. This will avoid many headaches and mistakes down the road.

GD <- function(x, y, alpha, n = nrow(x)){
  idx <- sample(nrow(x), n)
  y <- y[idx, , drop = FALSE]
  x <- x[idx, , drop = FALSE]
  theta <- matrix(c(0,0,0), nrow=1)
  theta_r <- NULL

  for (i in 1:500) {
    theta <- theta - alpha*cost(x,y,theta)  
    theta_r <- rbind(theta_r,theta)    
  }
  return(theta_r)
}

Splitlevel

This is exactly what I was trying to do. Your comment about explicitly passing arguments is going to save me so much fiddling later too. – Valeryvalerye

@Valeryvalerye glad this helps. you were doing the same thing with theta_r, so I added the initialization of that variable inside GD as well – Splitlevel