How to check if colorbar exists on figure

Question

Question: Is there a way to check if a color bar already exists?

I am making many plots with a loop. The issue is that the color bar is drawn every iteration!

If I could determine if the color bar exists then I can put the color bar function in an if statement.

if cb_exists:
    # do nothing
else:
    plt.colorbar() #draw the colorbar

If I use multiprocessing to make the figures, is it possible to prevent multiple color bars from being added?

import numpy as np
import matplotlib.pyplot as plt
import multiprocessing

def plot(number):
    a = np.random.random([5,5])*number
    plt.pcolormesh(a)
    plt.colorbar()
    plt.savefig('this_'+str(number))

# I want to make a 50 plots
some_list = range(0,50)
num_proc = 5
p = multiprocessing.Pool(num_proc)
temps = p.map(plot, some_list)

I realize I can clear the figure with plt.clf() and plt.cla() before plotting the next iteration. But, I have data on my basemap layer I don't want to re-plot (that adds to the time it takes to create the plot). So, if I could remove the colorbar and add a new one I'd save some time.

Pervade

can you show the code where it is created every iteration – Brae

One would need to know how exactly you create the plot. Is there more than one subplot per figure? – Donyadoodad

Seeing the update, what do you need the loop for? Just don't use the loop and you'll be fine. – Donyadoodad

Even with loop you can just use if i == 0: plt.colorbar() and thereby plotting the colorbar only in the first run of the loop. – Donyadoodad

@Donyadoodad I loop because the value of what is plotted changes each loop, but my plotting method doesn't matter. My question is: how do I remove the color bar from a figure after it has been drawn. – Pervade

So what's wrong with only creating a colorbar in the first run of the loop? Also you did not answer myfirst question: Is there more than one subplot per figure? – Donyadoodad

@Donyadoodad Just one subplot per figure. Also, if I'm using multiprocessing (see edit to question) I'm not sure how to only draw a colorbar on the first iteration. – Pervade

@Pervade As you can see in the update to my answer, multiprocessing actually works even when referencing some plot variables from outside. This is very supprising to me. But it also means that you can actually work without checking for the colorbar to exist or not and instead simply update it as required. – Donyadoodad

Answer 1

Is is actually not easy to remove a colorbar from a plot and later draw a new one to it. The best solution I can come up with at the moment is the following, which assumes that there is only one axes present in the plot. Now, if there was a second axis, it must be the colorbar beeing present. So by checking how many axes we find on the plot, we can judge upon whether or not there is a colorbar.

Here we also mind the user's wish not to reference any named objects from outside. (Which does not makes much sense, as we need to use plt anyways, but hey.. so was the question)

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
im = ax.pcolormesh(np.array(np.random.rand(2,2) ))
ax.plot(np.cos(np.linspace(0.2,1.8))+0.9, np.sin(np.linspace(0.2,1.8))+0.9, c="k", lw=6)
ax.set_title("Title")
cbar = plt.colorbar(im)
cbar.ax.set_ylabel("Label")


for i in range(10):
    # inside this loop we should not access any variables defined outside
    #   why? no real reason, but questioner asked for it.
    #draw new colormesh
    im = plt.gcf().gca().pcolormesh(np.random.rand(2,2))
    #check if there is more than one axes
    if len(plt.gcf().axes) > 1: 
        # if so, then the last axes must be the colorbar.
        # we get its extent
        pts = plt.gcf().axes[-1].get_position().get_points()
        # and its label
        label = plt.gcf().axes[-1].get_ylabel()
        # and then remove the axes
        plt.gcf().axes[-1].remove()
        # then we draw a new axes a the extents of the old one
        cax= plt.gcf().add_axes([pts[0][0],pts[0][1],pts[1][0]-pts[0][0],pts[1][1]-pts[0][1]  ])
        # and add a colorbar to it
        cbar = plt.colorbar(im, cax=cax)
        cbar.ax.set_ylabel(label)
        # unfortunately the aspect is different between the initial call to colorbar 
        #   without cax argument. Try to reset it (but still it's somehow different)
        cbar.ax.set_aspect(20)
    else:
        plt.colorbar(im)

plt.show()

---

In general a much better solution would be to operate on the objects already present in the plot and only update them with the new data. Thereby, we suppress the need to remove and add axes and find a much cleaner and faster solution.

import matplotlib.pyplot as plt
import numpy as np

fig, ax = plt.subplots()
im = ax.pcolormesh(np.array(np.random.rand(2,2) ))
ax.plot(np.cos(np.linspace(0.2,1.8))+0.9, np.sin(np.linspace(0.2,1.8))+0.9, c="k", lw=6)
ax.set_title("Title")
cbar = plt.colorbar(im)
cbar.ax.set_ylabel("Label")


for i in range(10):
    data = np.array(np.random.rand(2,2) )
    im.set_array(data.flatten())
    cbar.set_clim(vmin=data.min(),vmax=data.max()) 
    cbar.draw_all() 
    plt.draw()

plt.show()

---

Update:

Actually, the latter approach of referencing objects from outside even works together with the multiprocess approach desired by the questioner.

So, here is a code that updates the figure, without the need to delete the colorbar.

import matplotlib.pyplot as plt
import numpy as np
import multiprocessing
import time

fig, ax = plt.subplots()
im = ax.pcolormesh(np.array(np.random.rand(2,2) ))
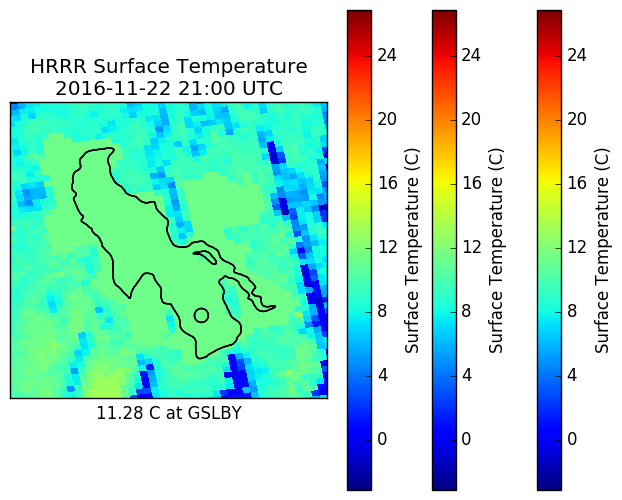
ax.plot(np.cos(np.linspace(0.2,1.8))+0.9, np.sin(np.linspace(0.2,1.8))+0.9, c="w", lw=6)
ax.set_title("Title")
cbar = plt.colorbar(im)
cbar.ax.set_ylabel("Label")
tx = ax.text(0.2,0.8, "", fontsize=30, color="w")
tx2 = ax.text(0.2,0.2, "", fontsize=30, color="w")

def do(number):
    start = time.time()
    tx.set_text(str(number))
    data = np.array(np.random.rand(2,2)*(number+1) )
    im.set_array(data.flatten())
    cbar.set_clim(vmin=data.min(),vmax=data.max()) 
    tx2.set_text("{m:.2f} < {ma:.2f}".format(m=data.min(), ma= data.max() )) 
    cbar.draw_all() 
    plt.draw()
    plt.savefig("multiproc/{n}.png".format(n=number))
    stop = time.time()

    return np.array([number, start, stop])


if __name__ == "__main__":
    multiprocessing.freeze_support()

    some_list = range(0,50)
    num_proc = 5
    p = multiprocessing.Pool(num_proc)
    nu = p.map(do, some_list)
    nu = np.array(nu)

    plt.close("all")
    fig, ax = plt.subplots(figsize=(16,9))
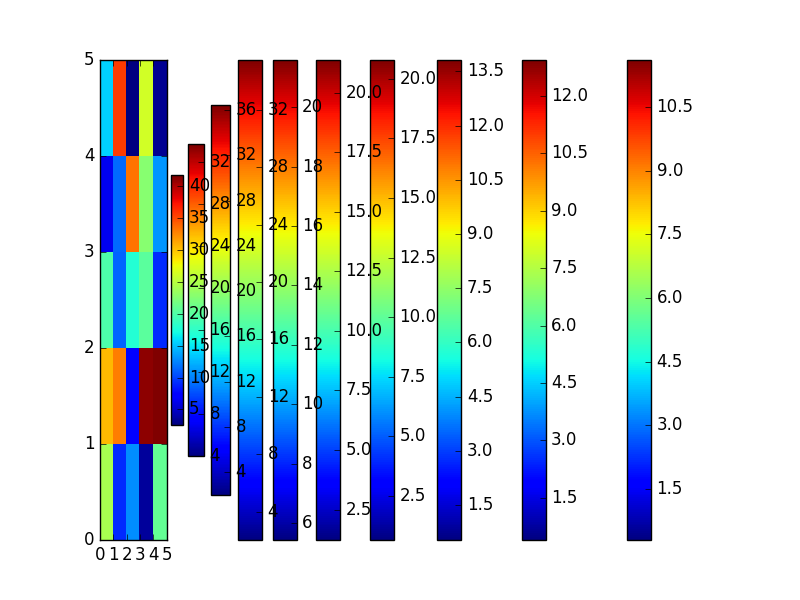
    ax.barh(nu[:,0], nu[:,2]-nu[:,1], height=np.ones(len(some_list)), left=nu[:,1],  align="center")
    plt.show()

(The code at the end shows a timetable which allows to see that multiprocessing has indeed taken place)

Donyadoodad

@ ImportanceOfBeingErnest Thanks for your updated solution. This method to update the objects works for me and even helps me understand how to deal with the plotting objects. – Pervade

It seems like none of these solutions works anymore with matplotlib version 3. Colorbars are lacking the set_clim method now, because the used to inherit from ScalarMappable in version 2, but are not inheriting from it in version 3. – Midpoint

Answer 2

If you can access to axis and image information, colorbar can be retrieved as a property of the image (or the mappable to which associate colorbar).

Following a previous answer (How to retrieve colorbar instance from figure in matplotlib), an example could be:

ax=plt.gca()        #plt.gca() for current axis, otherwise set appropriately.
im=ax.images        #this is a list of all images that have been plotted
if im[-1].colorbar is None:   #in this case I assume to be interested to the last one plotted, otherwise use the appropriate index or loop over
    plt.colorbar() #plot a new colorbar

Note that an image without colorbar returns None to im[-1].colorbar

Masao

Answer 3

One approach is:

1. initially (prior to having any color bar drawn), set a variable

   colorBarPresent = False
   

2. in the method for drawing the color bar, check to see if it's already drawn. If not, draw it and set the colorBarPresent variable True:

   def drawColorBar():
       if colorBarPresent:
           # leave the function and don't draw the bar again
       else:
           # draw  the color bar
           colorBarPresent = True
   

Memorandum

Yes, this is a simple solution. But I am creating plots using multiprocessing to makes lots of plots really fast, and communicating this variable to all the processors is difficult. That is why I just need to check if a colorbar already exists. – Pervade

@Pervade I would guess that if you always use plt and use the same figure to plot to, you are not actually using multiprocessing. – Donyadoodad

Answer 4

There is an indirect way of guessing (with reasonable accuracy for most applications, I think) whether an Axes instance is home to a color bar. Depending on whether it is a horizontal or vertical color bar, either the X axis or Y axis (but not both) will satisfy all of these conditions:

• No ticks
• No tick labels
• No axis label
• Axis range is (0, 1)

So here's a function for you:

def is_colorbar(ax):
    """
    Guesses whether a set of Axes is home to a colorbar

    :param ax: Axes instance

    :return: bool
        True if the x xor y axis satisfies all of the following and thus looks like it's probably a colorbar:
            No ticks, no tick labels, no axis label, and range is (0, 1)
    """
    xcb = (len(ax.get_xticks()) == 0) and (len(ax.get_xticklabels()) == 0) and (len(ax.get_xlabel()) == 0) and \
          (ax.get_xlim() == (0, 1))
    ycb = (len(ax.get_yticks()) == 0) and (len(ax.get_yticklabels()) == 0) and (len(ax.get_ylabel()) == 0) and \
          (ax.get_ylim() == (0, 1))
    return xcb != ycb  # != is effectively xor in this case, since xcb and ycb are both bool

Thanks to this answer for the cool != xor trick: https://mcmap.net/q/53241/-how-do-you-get-the-logical-xor-of-two-variables-in-python

With this function, you can see if a colorbar exists by:

colorbar_exists = any([is_colorbar(ax) for ax in np.atleast_1d(gcf().axes).flatten()])

or if you're sure the colorbar will always be last, you can get off easy with:

colorbar_exists = is_colorbar(gcf().axes[-1])

Robles