expand 1 dim vector by using taylor series of log(1+e^x) in python

Question

I need to non-linearly expand on each pixel value from 1 dim pixel vector with taylor series expansion of specific non-linear function (e^x or log(x) or log(1+e^x)), but my current implementation is not right to me at least based on taylor series concepts. The basic intuition behind is taking pixel array as input neurons for a CNN model where each pixel should be non-linearly expanded with taylor series expansion of non-linear function.

new update 1:

From my understanding from taylor series, taylor series is written for a function F of a variable x in terms of the value of the function F and it's derivatives in for another value of variable x0. In my problem, F is function of non-linear transformation of features (a.k.a, pixels), x is each pixel value, x0 is maclaurin series approximation at 0.

new update 2

if we use taylor series of log(1+e^x) with approximation order of 2, each pixel value will yield two new pixel by taking first and second expansion terms of taylor series.

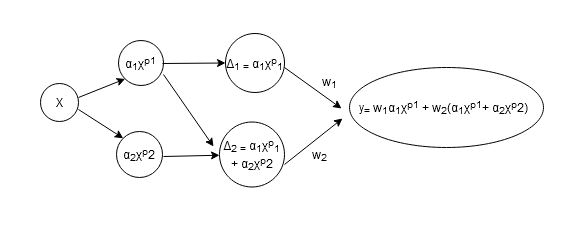
graphic illustration

Here is the graphical illustration of the above formulation:

Where X is pixel array, p is approximation order of taylor series, and α is the taylor expansion coefficient.

I wanted to non-linearly expand pixel vectors with taylor series expansion of non-linear function like above illustration demonstrated.

My current attempt

This is my current attempt which is not working correctly for pixel arrays. I was thinking about how to make the same idea applicable to pixel arrays.

def taylor_func(x, approx_order=2):
    x_ = x[..., None] 
    x_ = tf.tile(x_, multiples=[1, 1, approx_order+ 1])  
    pows = tf.range(0, approx_order + 1, dtype=tf.float32) 
    x_p = tf.pow(x_, pows) 
    x_p_ = x_p[..., None]
    return x_p_

x = Input(shape=(4,4,3))
x_new = Lambda(lambda x: taylor_func(x, max_pow))(x)

my new updated attempt:

x_input= Input(shape=(32, 32,3))

def maclurin_exp(x, powers=2):
    out= 0
    for k in range(powers):
        out+= ((-1)**k) * (x ** (2*k)) / (math.factorial(2 * k))
    return res

x_input_new = Lambda(lambda x: maclurin_exp(x, max_pow))(x_input)

This attempt doesn't yield what the above mathematical formulation describes. I bet I missed something while doing the expansion. Can anyone point me on how to make this correct? Any better idea?

goal

I wanted to take pixel vector and make non-linearly distributed or expanded with taylor series expansion of certain non-linear function. Is there any possible way to do this? any thoughts? thanks

Ambi

Hi Jared, could you please clarify your idea? I do not understand the equation you have written. Are you trying to replace an input image of a size N by M with pixel values x[i] by a concatenated array of a size pN by M with blocks of elements of a form x[i]**k, with k=1...p, and p as a truncation power of Taylor series? – Lathrop

I guess this is the part that I do not exactly understand. Taylor series are written for a function F of a variable x in terms of the value of the function F and it's derivatives in for another value of variable x0. So it is unclear to me what is the function and what is the variable when you say expand pixel vector with Taylor series expansion. Does the function represent the value of the pixel, while the variable are its coordinates in a 2D array (discrete values)? – Lathrop

I do not understand the concept of function is Taylor expansion of non-linear function. Consider a simple power 2 truncated Taylor series, as it is in your original post F(x) = F(x0) + F'(x0)*(x-x0) + 0.5*F''(x0)*(x-x0)**2 . What F, x and x0 are here? If x is the original image, then what x0 is? – Lathrop

the same way you were doing it - just append pixel values to power 2 to your original input. Biases would be equivalent to x0, so you get that term for free. Except I would probably do something like x2 = tf.pow(x, 2) followed by x_tot = tf.concat([x, x2], axis = -2) and use that as an input. But I do not think that there is any benefit in it, as non-linear transforms in activation function tend to give you powers of your inputs. – Lathrop

@Jared I have a question for you. It seems like you are looking to essentially double the pixel value of a photo. Is that correct? I ask because I would think you would need to square it because you have both the x-axis and the y-axis to account for. – Valdivia

I have some thoughts. The first is log(0) and ln(0) are asymptotic to negative infinity. Also, I'm doing a Taylor series expansion as it's more flexible. But I should have something for you tonight or tomorrow. And a private chat is fine. – Valdivia

Just so you know, I'm working on it and shooting to give you the most flexible and complete answer I can given what I understand the question to be. I'm focusing on the code first as that's the question you asked. As for splining, I'd kind of need to see that would piece into what you're doing. – Valdivia

I already rathered that from what you wrote before. I'm assuming this what you want to use as the activation function. – Valdivia

@Valdivia thanks. Any canonical answer you might have for this? – Ambi

Let us continue this discussion in chat. – Ambi

Answer 1

This is a really interesting question but I can't say that I'm clear on it as of yet. So, while I have some thoughts, I might be missing the thrust of what you're looking to do.

It seems like you want to develop your own activation function instead of using something RELU or softmax. Certainly no harm there. And you gave three candidates: e^x, log(x), and log(1+e^x).

Notice log(x) asymptotically approaches negative infinity x --> 0. So, log(x) is right out. If that was intended as a check on the answers you get or was something jotted down as you were falling asleep, no worries. But if it wasn't, you should spend some time and make sure you understand the underpinnings of what you doing because the consequences can be quite high.

You indicated you were looking for a canonical answer and you get a two for one here. You get both a canonical answer and highly performant code.

Considering you're not likely to able to write faster, more streamlined code than the folks of SciPy, Numpy, or Pandas. Or, PyPy. Or Cython for that matter. Their stuff is the standard. So don't try to compete against them by writing your own, less performant (and possibly bugged) version which you will then have to maintain as time passes. Instead, maximize your development and run times by using them.

Let's take a look at the implementation e^x in SciPy and give you some code to work with. I know you don't need a graph for what you're at this stage but they're pretty and can help you understand how they Taylor (or Maclaurin, aka Euler-Maclaurin) will work as the order of the approximation changes. It just so happens that SciPy has Taylor approximation built-in.

import scipy
import numpy as np
import matplotlib.pyplot as plt

from scipy.interpolate import approximate_taylor_polynomial

x = np.linspace(-10.0, 10.0, num=100)

plt.plot(x, np.exp(x), label="e^x", color = 'black')

for degree in np.arange(1, 4, step=1):

    e_to_the_x_taylor = approximate_taylor_polynomial(np.exp, 0, degree, 1, order=degree + 2)

    plt.plot(x, e_to_the_x_taylor(x), label=f"degree={degree}")

plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.0, shadow=True)

plt.tight_layout()
plt.axis([-10, 10, -10, 10])
plt.show()

That produces this:

But let's say if you're good with 'the maths', so to speak, and are willing to go with something slightly slower if it's more 'mathy' as in it handles symbolic notation well. For that, let me suggest SymPy.

And with that in mind here is a bit of SymPy code with a graph because, well, it looks good AND because we need to go back and hit another point again.

from sympy import series, Symbol, log, E
from sympy.functions import exp
from sympy.plotting import plot
import matplotlib.pyplot as plt
%matplotlib inline

plt.rcParams['figure.figsize'] = 13,10
plt.rcParams['lines.linewidth'] = 2

x = Symbol('x')

def taylor(function, x0, n):
    """ Defines Taylor approximation of a given function
    function -- is our function which we want to approximate
    x0 -- point where to approximate
    n -- order of approximation
    """    
    return function.series(x,x0,n).removeO()

# I get eyestain; feel free to get rid of this
plt.rcParams['figure.figsize'] = 10, 8
plt.rcParams['lines.linewidth'] = 1

c = log(1 + pow(E, x))

plt = plot(c, taylor(c,0,1), taylor(c,0,2), taylor(c,0,3), taylor(c,0,4), (x,-5,5),legend=True, show=False)

plt[0].line_color = 'black'
plt[1].line_color = 'red'
plt[2].line_color = 'orange'
plt[3].line_color = 'green'
plt[4].line_color = 'blue'
plt.title = 'Taylor Series Expansion for log(1 +e^x)'
plt.show()

I think either option will get you where you need go.

Ok, now for the other point. You clearly stated after a bit of revision that log(1 +e^x) was your first choice. But the others don't pass the sniff test. e^x vacillates wildly as the degree of the polynomial changes. Because of the opaqueness of algorithms and how few people can conceptually understand this stuff, Data Scientists can screw things up to a degree people can't even imagine. So make sure you're very solid on theory for this.

One last thing, consider looking at the CDF of the Erlang Distribution as an activation function (assuming I'm right and you're looking to roll your own activation function as an area of research). I don't think anyone has looked at that but it strikes as promising. I think you could break out each channel of the RGB as one of the two parameters, with the other being the physical coordinate.

Valdivia

Answer 2

You can use tf.tile and tf.math.pow to generate the elements of the series expansion. Then you can use tf.math.cumsum to compute the partial sums s_i. Eventually you can multiply with the weights w_i and compute the final sum.

Here is a code sample:

import math
import tensorflow as tf

x = tf.keras.Input(shape=(32, 32, 3))  # 3-channel RGB.

# The following is determined by your series expansion and its order.
# For example: log(1 + exp(x)) to 3rd order.
# https://www.wolframalpha.com/input/?i=taylor+series+log%281+%2B+e%5Ex%29
order = 3
alpha = tf.constant([1/2, 1/8, -1/192])  # Series coefficients.
power = tf.constant([1.0, 2.0, 4.0])
offset = math.log(2)

# These are the weights of the network; using a constant for simplicity here.
# The shape must coincide with the above order of series expansion.
w_i = tf.constant([1.0, 1.0, 1.0])

elements = offset + alpha * tf.math.pow(
    tf.tile(x[..., None], [1, 1, 1, 1, order]),
    power
)
s_i = tf.math.cumsum(elements, axis=-1)
y = tf.math.reduce_sum(w_i * s_i, axis=-1)

Selaginella

@Jared It's the elements tensor which represents the elements of the series expansion. It has shape (?, 32, 32, 3, order) where order is the order of the series expansion. So the first term is elements[..., 0] and the second term is elements[..., 1] and so on. – Selaginella

@Jared What is delta1 and delta2? Where is it defined? – Selaginella

it is showed above graph in my post. delta1 is first Taylor expansion terms, delta2 is sum of first and second expansion terms. I'd like to delta1 and delta2 as two newly expanded neurons that going to be passed to convolutional filter independently. Would it be possible to extend your thought if it is possible? Thank you very much! – Ambi

@Jared Sure, that would be s_i in the above code. It's the cumulative sum along the axis of all series elements, so s_i[..., 0] is just the first term, s_i[..., 1] is the sum of first and second term and so on. – Selaginella

Let us continue this discussion in chat. – Ambi

why is this line: elements = offset + alpha * tf.math.pow(tf.tile(x[:, None, ...], [1, order, 1, 1, 1]), power[:, None, None, None]) hard coded for order 3? what if we expand it with only two expansion term? what generic code would be? Thanks for your canonical answer !!! – Ambi

@Jared It is not hardcoded for a specific order, it works for any order. The size of the last dimension determines the order. – Selaginella