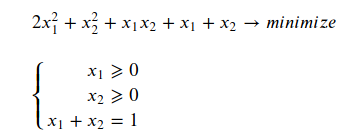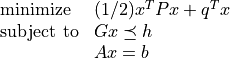how Python cvxopt solvers qp basically works

Question

I want to use cvxopt solvers qp and compute Lagrange multiplier but I wonder how it works "exactly". I was trying to find more information but there is not much information about cvxopt out there. I was looking at this example problem and I am not sure what these variables signify and how they come up with a solution.

The example is like this:

can be solved by using

Q = 2*matrix([ [2, .5], [.5, 1] ])
p = matrix([1.0, 1.0])
G = matrix([[-1.0,0.0],[0.0,-1.0]])
h = matrix([0.0,0.0])
A = matrix([1.0, 1.0], (1,2))
b = matrix(1.0)
sol=solvers.qp(Q, p, G, h, A, b)
print(sol['x'])

Highbinder

Answer 1

You should have a look at this:

Solving QP with CVXopt

For solving a quadratic programming problem, CVXopt accepts a set of matrices, generally mentioned as P,q,G,A, and h. You have to first convert your problem into the specific form accepted by CVXopt (mentioned in the link). The aim is to find an optimal solution, (in your case, Lagrange multipliers) which is the matrix 'x'.

The object in which you 'store' the solution has a number of properties, one of which is the matrix 'x', which you can print or use for further calculations.

Zacharie

The provided link seems to be broken. – Stylo

Answer 2

I'm not sure yet how the full setup works, but the basic setup is like the following. I am using this example from the docs.

• c is the function we want to minimize, 2x1 + x2 = [2,1]
• b (AKA h) is the value on the right hand side of the constraints.
• A (AKA G) are the coefficients of the constraint equations.

Constraint equations are

• -x1 + x2 <= 1
• x1 + x2 >= 2
• x2 >= 0
• x1-2x2 <= 4

Any constraints that are >= must be multiplied by -1 to become a <=.

So b=[1,-2,0,4] And

A = [ 
  [-1.0, -1.0, 0.0, 1.0], #x1
  [1.0, -1.0, -1.0, -2.0] #x2
]

Solve with

>>> from cvxopt import matrix, solvers
#wrap our arrays in the `matrix` function
>>> sol=solvers.lp(c,A,b)
>>> print(sol['x'])
[ 5.00e-01]
[ 1.50e+00]

Stearn

Answer 3

This solves a quadratic program (QP) in the following standard from,

Explanation about the standard form of Quadratic Program in cvxopt package can be found in the code documentation. But, this does not clearly specify outputs. Further detailed explanation can be found in the documentation provided in the code comments.

Emalee