adding regression line to a plot given its intercept and slope

Question

Using the following small dataset:

bill = [34,108,64,88,99,51]
tip =  [5,17,11,8,14,5]  

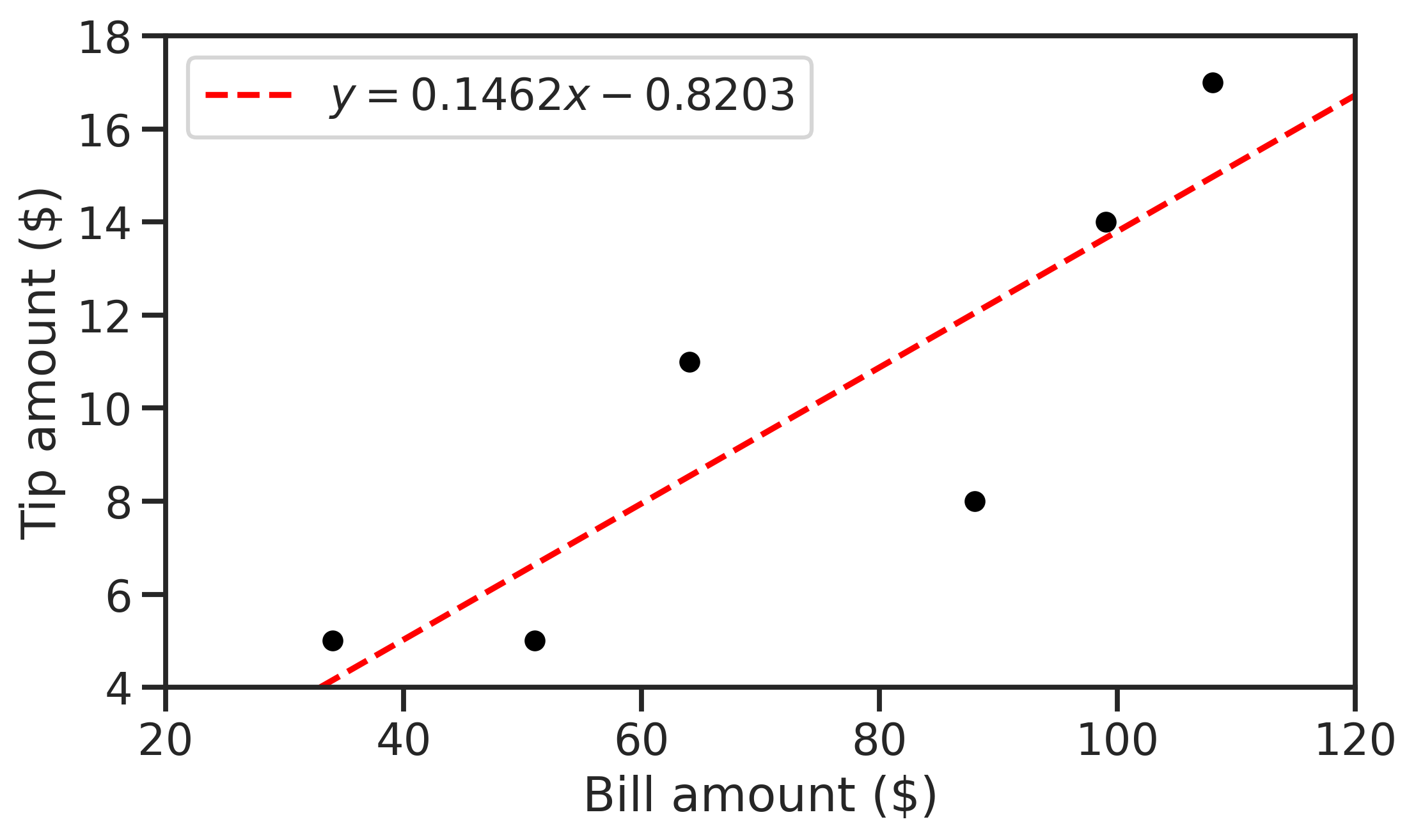
I calculated a best-fit regression line (by hand).

yi = 0.1462*x - 0.8188 #yi = slope(x) + intercept

I've plotted my original data using Matplotlib like this:

plt.scatter(bill,tip, color="black")
plt.xlim(20,120) #set ranges
plt.ylim(4,18)

#plot centroid point (mean of each variable (74,10))
line1 = plt.plot([74, 74],[0,10], ':', c="red")
line2 = plt.plot([0,74],[10,10],':', c="red")

plt.scatter(74,10, c="red")

#annotate the centroid point
plt.annotate('centroid (74,10)', xy=(74.1,10), xytext=(81,9),
        arrowprops=dict(facecolor="black", shrink=0.01),
        )

#label axes
plt.xlabel("Bill amount ($)")
plt.ylabel("Tip amount ($)")

#display plot
plt.show()

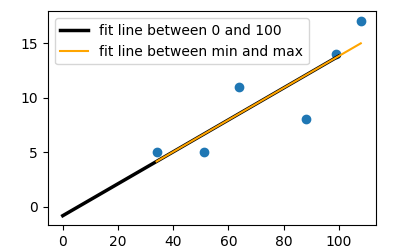
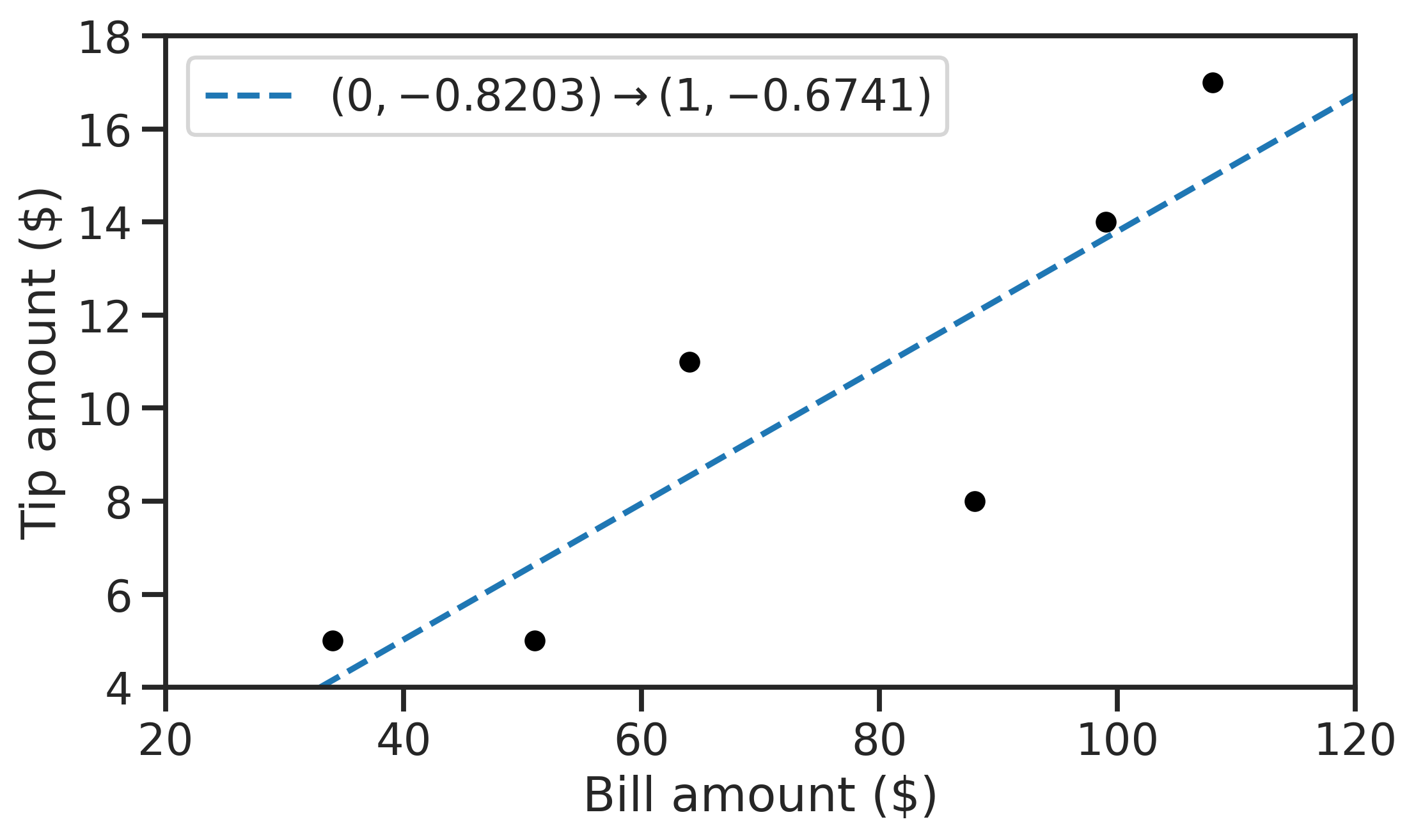
I am unsure how to get the regression line onto the plot itself. I'm aware that there are plenty of builtin stuff for quickly fitting and displaying best fit lines, but I did this as practice. I know I can start the line at points '0,0.8188' (the intercept), but I don't know how to use the slope value to complete the line (set the lines end points).

Given that for each increase on the x axis, the slope should increase by '0.1462'; for the line coordinates I tried (0,0.8188) for the starting point, and (100,14.62) for the end point. But this line does not pass through my centroid point. It just misses it.

Telespectroscope

Answer 1

The reasoning in the question partially correct. Having a function f(x) = a*x +b, you may take as first point the interception with the y axis (x=0) as (0, b) (or (0,-0.8188) in this case).
Any other point on that line is given by (x, f(x)), or (x, a*x+b). So looking at the point at x=100 would give you (100, f(100)), plugging in: (100, 0.1462*100-0.8188) = (100,13.8012). In the case you describe in the question you just forgot to take the b into account.

The following shows how to use that function to plot the line in matplotlib:

import matplotlib.pyplot as plt
import numpy as np

bill = [34,108,64,88,99,51]
tip =  [5,17,11,8,14,5]  
plt.scatter(bill, tip)

#fit function
f = lambda x: 0.1462*x - 0.8188
# x values of line to plot
x = np.array([0,100])
# plot fit
plt.plot(x,f(x),lw=2.5, c="k",label="fit line between 0 and 100")

#better take min and max of x values
x = np.array([min(bill),max(bill)])
plt.plot(x,f(x), c="orange", label="fit line between min and max")

plt.legend()
plt.show()

Of course the fitting can also be done automatically. You can obtain the slope and intercept from a call to numpy.polyfit:

#fit function
a, b = np.polyfit(np.array(bill), np.array(tip), deg=1)
f = lambda x: a*x + b

The rest in the plot would stay the same.

Trapp

Answer 2

New in matplotlib 3.3.0

plt.axline now makes it much easier to plot a regression line (or any arbitrary infinite line).

---

• Slope-intercept form

  This is simplest for regression lines. Use np.polyfit to compute the slope m and intercept b and plug them into plt.axline:

  # y = m * x + b
  m, b = np.polyfit(x=bill, y=tip, deg=1)
  plt.axline(xy1=(0, b), slope=m, label=f'$y = {m}x {b:+}$')
  

---

• Point-slope form

  If you have some other arbitrary point (x1, y1) along the line, it can also be used with the slope:

  # y - y1 = m * (x - x1)
  x1, y1 = (1, -0.6741)
  plt.axline(xy1=(x1, y1), slope=m, label=f'$y {-y1:+} = {m}(x {-x1:+})$')
  

---

• Two points

  It's also possible to use any two arbitrary points along the line:

  xy1 = (1, -0.6741)
  xy2 = (0, -0.8203)
  plt.axline(xy1=xy1, xy2=xy2, label=f'${xy1} \\rightarrow {xy2}$')
  

---

Also see How to annotate a regression line with the proper text rotation.

Spawn

Answer 3

define function fit, get endpoints of data, put in tuples to plot()

def fit(x):
    return 0.1462*x - 0.8188 #yi = slope(x) - intercept
xfit, yfit = (min(bill), max(bill)), (fit(min(bill)), fit(max(bill)))    
plt.plot(xfit, yfit,'b')

Ciborium