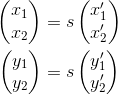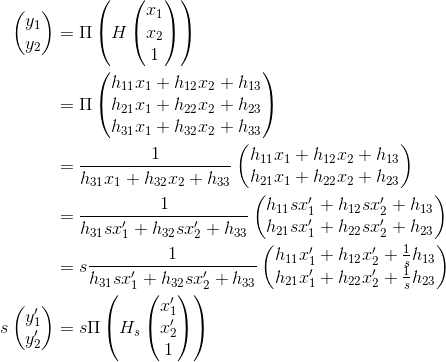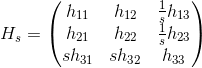How to change the homography with the scale of the image?

Question

I have two planar images A and B I have calculated the homography between these two images using feature points, my question is, if both A and B scale up to double size, let's say A' and B'. How will homography' be? Thank you.

Hammerskjold

Answer 1

The homography doesn't change. It will be the same as long as both images have undergone the same linear scaling.

The homography is a mapping between two 2D planes in 3D space. It combines at rotation and translation with the camera matrix. If the position of the camera relative to the object has not changed, then a homography calculated from a mapping of points in the object plane to the equivalent points in the image plane will be the same (assuming no noise) regardless of the points chosen.

Bumbling

I don't think so, the homography includes rotation and translation, I think the translation must be different. – Hammerskjold

@Hammerskjold I've expanded my answer - maybe I misunderstood your question. I'm assuming that the images are scaled about their centres, so the translation doesn't change. – Bumbling

thank you. Now let's assumed the homography does not changed, say H = [a11, a12, a13, a21, a22, a23, a31, a32, a33], Then mapping of points from image B to image A would be: – Hammerskjold

Thank you. Now let's assumed the homography does not changed, say H = [a11, a12, a13, a21, a22, a23, a31, a32, a33], Then mapping of points from image a(xa,ya) to image B(xb, yb) would be: xb = (a11*xa+a12*ya+a13)/(a31*xa+a32*ya+a33), If both the images scale up to double size, the mapping would be (2xa,2ya)-->(2xb,2yb) 2xb = (a11*2xa+ a12*2ya + a13) / (a31*2xa + a32*2ya + a33). It conflicts with the above equation of (xa,ya)->(xb,yb) – Hammerskjold

@Hammerskjold Ok I think I see what you mean. If image A is scaled to double size about its centre, then image B must be scaled to double about the projected centre of image A. This is where the translation offset arises, yes? – Bumbling

I think I also understand what you mean. Thank you. – Hammerskjold

Could someone give feedback about which technique worked? Or which way worked better? @Hammerskjold – Devisable

Answer 2

The two answers are wrong! Sorry!

The right answer with proof is:

Anaanabaena

Applying a homography is nonlinear. This proof is insufficient. Let's say you have scale s1 and scale s2 (s1 < s2), you have the homography for s1 and you have points in s2 which you want to project. Option 1: scale points down, apply homography in s1, then scale points back up. (probably what you mean, but incorrect proof) Option 2: "scale homography up", apply homography in s2 directly. (my answer) – Chiropteran

dear @jns, if you read the proof carefully, you will notice that I didn't change any image (scale and rescale as you mentioned), I just derived a formula for the homography matrix of the second image without making any assumptions, the demonstration is general. – Anaanabaena

Well, you define H' to be "scale inversly" (S^-1), "apply homography" (H) and then "scale back" (S). The problem is that applying a homography to 2d points is not a linear transformation. – Chiropteran

i can't comment on jns' objection above, but schlodinger's answer works in my app while jns' doesn't. maybe i'm making a mistake implementing jns' but that's what i find. for context: in my app i take two images and scale them down and find and match keypoints between them (scaling down makes this a lot faster), then i find the homography between the scaled down images. i then want to alter the found homography so that it works between the two original (full size) images. i would call that "scaling up the homography" but maybe that isn't technically accurate as a name. – Suffruticose

The solution is working great for me. Thanks very much. Does anyone know where this solution is mentioned in literature ? I would need a quotable source – Rosinski

@Rosinski I remember that I couldn't find this formula in literature, and I just did the proof myself – Anaanabaena

Answer 3

I think you can modify the homography for the correct scale. Let's assume correspondences are denoted with x and y and the homography maps x to y. If we consider scaled points

we can try to factor s out of the transformation involving the homography matrix like so:

Where capital pi (Π) denotes the perspective transformation (simply dividing x and y component of a 3D vector with its z component). When cancelling s, we would have the equation necessary to apply the homography in a different scale. Here H_s can be read off the previous equation as:

If you compute a homography on a scale different from your "application scale" (e.g. visualization), you should be fine to just compute H_s where s is the relative factor from new scale (denoted with prime) to old scale. For instance, if a visualization is twice as large as the computation choose s = 0.5.

Chiropteran

Answer 4

Hmm.. I could be wrong, but I think both answers above are incorrect.

See https://en.wikipedia.org/wiki/Affine_transformation and What do the elements in a homography matrix mean?

As Wikipedia explains, the scale factor in the homography matrix H is

ScaleA = H[row = 0, column = 0] and ScaleB = H[row = 1, column = 1]

The translation (left, right, forward, back) would be

H[row = 0, column = 2] and H[row = 1, column = 2]

The remaining elements of the homography are rotational and shear components.

Yon