Geometric representation of Perceptrons (Artificial neural networks) [closed]

Question

I am taking this course on Neural networks in Coursera by Geoffrey Hinton (not current).

I have a very basic doubt on weight spaces. https://d396qusza40orc.cloudfront.net/neuralnets/lecture_slides%2Flec2.pdf Page 18.

If I have a weight vector (bias is 0) as [w1=1,w2=2] and training case as {1,2,-1} and {2,1,1} where I guess {1,2} and {2,1} are the input vectors. How can it be represented geometrically?

I am unable to visualize it? Why is training case giving a plane which divides the weight space into 2? Could somebody explain this in a coordinate axes of 3 dimensions?

The following is the text from the ppt:

1.Weight-space has one dimension per weight.

2.A point in the space has particular setting for all the weights.

3.Assuming that we have eliminated the threshold each hyperplane could be represented as a hyperplane through the origin.

My doubt is in the third point above. Kindly help me understand.

Warman

did you get my answer @kosmos? it's kinda hard to explain – Witenagemot

@Witenagemot still not clear. Please could you help me now as I provided additional information. – Warman

Answer 1

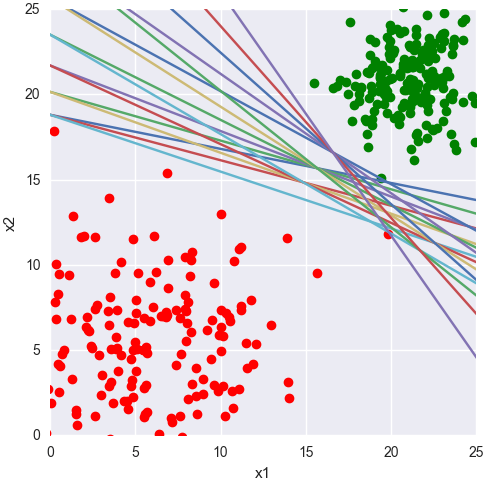
It's probably easier to explain if you look deeper into the math. Basically what a single layer of a neural net is performing some function on your input vector transforming it into a different vector space.

You don't want to jump right into thinking of this in 3-dimensions. Start smaller, it's easy to make diagrams in 1-2 dimensions, and nearly impossible to draw anything worthwhile in 3 dimensions (unless you're a brilliant artist), and being able to sketch this stuff out is invaluable.

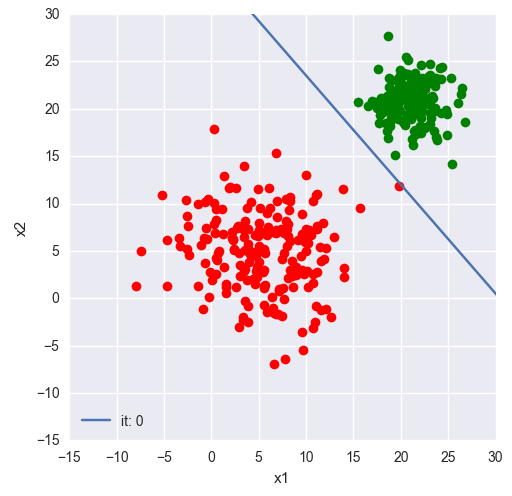
Let's take the simplest case, where you're taking in an input vector of length 2, you have a weight vector of dimension 2x1, which implies an output vector of length one (effectively a scalar)

In this case it's pretty easy to imagine that you've got something of the form:

input = [x, y]
weight = [a, b]
output = ax + by

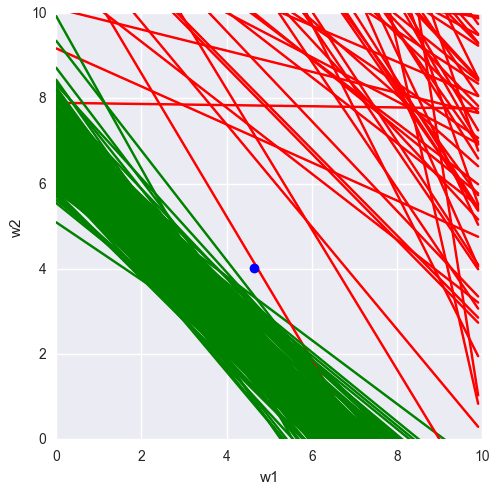
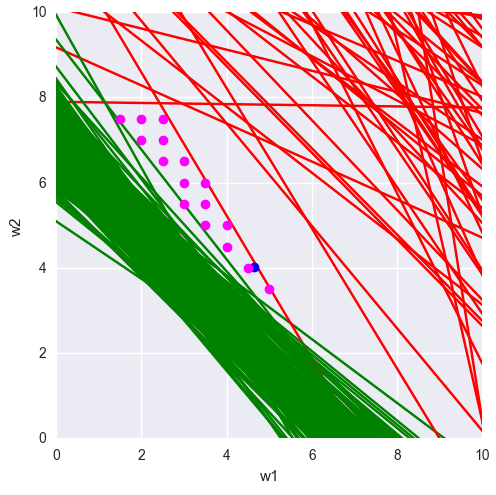
If we assume that weight = [1, 3], we can see, and hopefully intuit that the response of our perceptron will be something like this:

With the behavior being largely unchanged for different values of the weight vector.

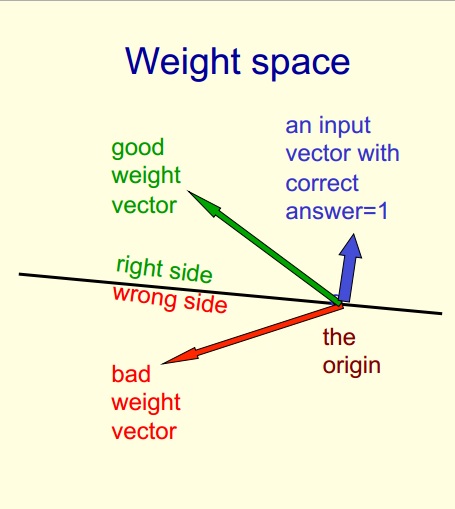
It's easy to imagine then, that if you're constraining your output to a binary space, there is a plane, maybe 0.5 units above the one shown above that constitutes your "decision boundary".

As you move into higher dimensions this becomes harder and harder to visualize, but if you imagine that that plane shown isn't merely a 2-d plane, but an n-d plane or a hyperplane, you can imagine that this same process happens.

Since actually creating the hyperplane requires either the input or output to be fixed, you can think of giving your perceptron a single training value as creating a "fixed" [x,y] value. This can be used to create a hyperplane. Sadly, this cannot be effectively be visualized as 4-d drawings are not really feasible in browser.

Hope that clears things up, let me know if you have more questions.

Fanechka

Thanks for your answer. I am still not able to relate your answer with this figure bu the instructor. Can you please help me map the two? i.sstatic.net/nzHSl.jpg – Warman

What is the 3rd dimension in your figure? And how is range for that [-5,5]? – Nealson

@KobyBecker The 3rd dimension is output. The range is dictated by the limits of x and y. Imagine that the true underlying behavior is something like 2x + 3y. I hope that helps. – Fanechka

Answer 2

I have encountered this question on SO while preparing a large article on linear combinations (it's in Russian, https://habrahabr.ru/post/324736/). It has a section on the weight space and I would like to share some thoughts from it.

Let's take a simple case of linearly separable dataset with two classes, red and green:

The illustration above is in the dataspace X, where samples are represented by points and weight coefficients constitutes a line. It could be conveyed by the following formula:

w^T * x + b = 0

But we can rewrite it vice-versa making x component a vector-coefficient and w a vector-variable:

x^T * w + b = 0

because dot product is symmetrical. Now it could be visualized in the weight space the following way:

where red and green lines are the samples and blue point is the weight.

More possible weights are limited to the area below (shown in magenta):

which could be visualized in dataspace X as:

Hope it clarifies dataspace/weightspace correlation a bit. Feel free to ask questions, will be glad to explain in more detail.

Arv

Answer 3

The "decision boundary" for a single layer perceptron is a plane (hyper plane)

where n in the image is the weight vector w, in your case w={w1=1,w2=2}=(1,2) and the direction specifies which side is the right side. n is orthogonal (90 degrees) to the plane)

A plane always splits a space into 2 naturally (extend the plane to infinity in each direction)

you can also try to input different value into the perceptron and try to find where the response is zero (only on the decision boundary).

Recommend you read up on linear algebra to understand it better: https://www.khanacademy.org/math/linear-algebra/vectors_and_spaces

Witenagemot

-0 This leaves out a LOT of critical information. Specifically, the fact that the input and output vectors are not of the same dimensionality, which is very crucial. – Fanechka

I understand vector spaces, hyperplanes. But I am not able to see how training cases form planes in the weight space. Could you please relate the given image i.sstatic.net/nzHSl.jpg to your explanation? – Warman

@SlaterTyranus it depends on how you are seeing the problem, your plane which represents the response over x, y or if you choose to only represent the decision boundary (in this case where the response = 0) which is a line. This line will have the "direction" of the weight vector. Disregarding bias or fiddling bias into the input you have sum(w_i*x_i) which is the "dot" product of w and x vector which is only zero when the vectors are ortagonal (i.e. on the decision hyperplane) – Witenagemot

I have finally understood it. Before you draw the geometry its important to tell whether you are drawing the weight space or the input space. I can either draw my input training hyperplane and divide the weight space into two or I could use my weight hyperplane to divide the input space into two in which it becomes the 'decision boundary'. As to why it passes through origin, it need not if we take threshold into consideration. but if threshold becomes another weight to be learnt, then we make it zero as you both must be already aware of. Thanks to you both for leading me to the solutions. – Warman

@Warman can you please provide a more detailed explanation? I'm on the same lecture and unable to understand what's going on here. – Nealson

what is the origin? – Muckworm

Please elaborate @YuriyPryyma Do you mean where I got my answer from? As I stated in the answer, it comes from linear algebra (no special source) – Witenagemot

@Witenagemot sorry. I mean there is point where all vectors come from if you look at image. This point is with text "The origin". What is this point? – Muckworm

If you look at the lecture notes PDF "Each training case defines a plane (shown as a black line) – The plane goes through the origin and is perpendicular to the input vector. – On one side of the plane the output is wrong because the scalar product of the weight vector with the input vector has the wrong sign. " Means that "The origin" is (0,0) since it's the only place where any training sample's plane (black line) will cross. I think it's what they mean. – Witenagemot

Answer 4

For a perceptron with 1 input & 1 output layer, there can only be 1 LINEAR hyperplane. And since there is no bias, the hyperplane won't be able to shift in an axis and so it will always share the same origin point. However, if there is a bias, they may not share a same point anymore.

Armful

Answer 5

I think the reason why a training case can be represented as a hyperplane because... Let's say [j,k] is the weight vector and [m,n] is the training-input

training-output = jm + kn

Given that a training case in this perspective is fixed and the weights varies, the training-input (m, n) becomes the coefficient and the weights (j, k) become the variables. Just as in any text book where z = ax + by is a plane, training-output = jm + kn is also a plane defined by training-output, m, and n.

Margie

Answer 6

Equation of a plane passing through origin is written in the form:

ax+by+cz=0

If a=1,b=2,c=3;Equation of the plane can be written as:

x+2y+3z=0

So,in the XYZ plane,Equation: x+2y+3z=0

Now,in the weight space;every dimension will represent a weight.So,if the perceptron has 10 weights,Weight space will be 10 dimensional.

Equation of the perceptron: ax+by+cz<=0 ==> Class 0

                          ax+by+cz>0  ==> Class 1

In this case;a,b & c are the weights.x,y & z are the input features.

In the weight space;a,b & c are the variables(axis).

So,for every training example;for eg: (x,y,z)=(2,3,4);a hyperplane would be formed in the weight space whose equation would be:

2a+3b+4c=0

passing through the origin.

I hope,now,you understand it.

Taryntaryne

Answer 7

Consider we have 2 weights. So w = [w1, w2]. Suppose we have input x = [x1, x2] = [1, 2]. If you use the weight to do a prediction, you have z = w1*x1 + w2*x2 and prediction y = z > 0 ? 1 : 0.

Suppose the label for the input x is 1. Thus, we hope y = 1, and thus we want z = w1*x1 + w2*x2 > 0. Consider vector multiplication, z = (w ^ T)x. So we want (w ^ T)x > 0. The geometric interpretation of this expression is that the angle between w and x is less than 90 degree. For example, the green vector is a candidate for w that would give the correct prediction of 1 in this case. Actually, any vector that lies on the same side, with respect to the line of w1 + 2 * w2 = 0, as the green vector would give the correct solution. However, if it lies on the other side as the red vector does, then it would give the wrong answer. However, suppose the label is 0. Then the case would just be the reverse.

The above case gives the intuition understand and just illustrates the 3 points in the lecture slide. The testing case x determines the plane, and depending on the label, the weight vector must lie on one particular side of the plane to give the correct answer.

Unswear