How to rotate a 3D surface

Question

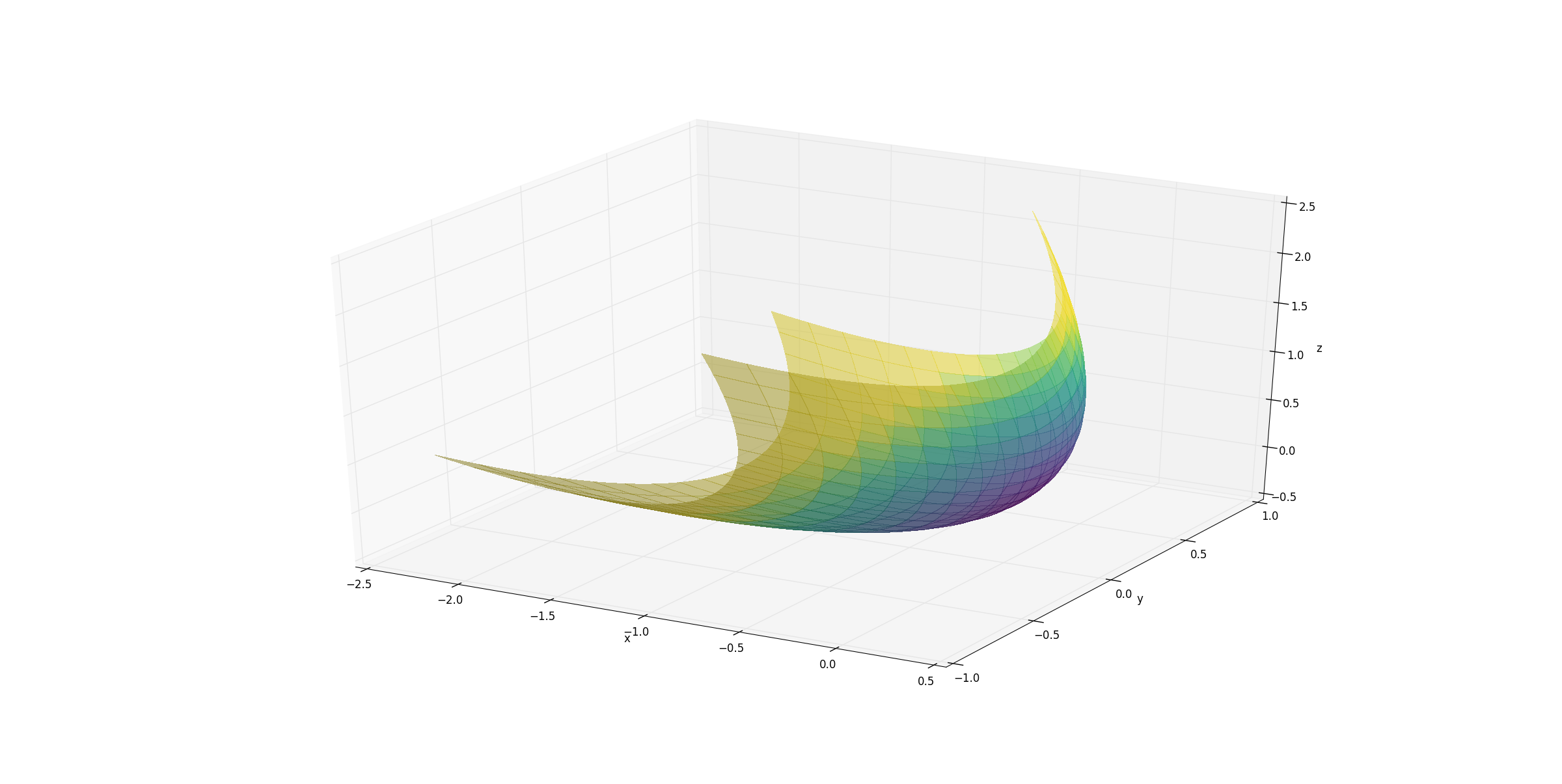
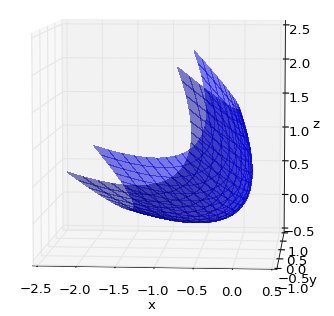
I have written code to plot a 3D surface of a parabaloid in matplotlib.

How would I rotate the figure so that the figure remains in place (i.e. no vertical or horizontal shifts) however it rotates around the line y = 0 and z = 0 through an angle of theta ( I have highlighted the line about which the figure should rotate in green). Here is an illustration to help visualize what I am describing:

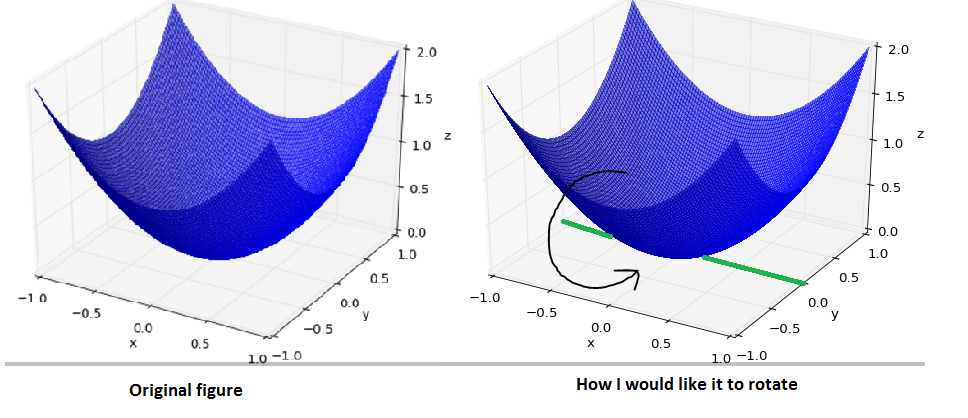
For example, If the figure were rotated about the line through an angle of 180 degrees then this would result in the figure being flipped 'upside down' so that the point at the origin would be now be the maximum point.

I would also like to rotate the axis so that the colormap is maintained. Here is the code for drawing the figure:

#parabaloid
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

#creating grid
y = np.linspace(-1,1,1000)
x = np.linspace(-1,1,1000)
x,y = np.meshgrid(x,y)

#set z values
z = x**2+y**2

#label axes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')


#plot figure
ax.plot_surface(x,y,z,linewidth=0, antialiased=False, shade = True, alpha = 0.5)

plt.show()

Pinzler

Do you want to rotate the axes too? – Xeres

In fact, yes I would, since I would like the colors to remains the same – Pinzler

Answer 1

Following my comment:

import mayavi.mlab as mlab
import numpy as np
x,y = np.mgrid[-1:1:0.001, -1:1:0.001]
z = x**2+y**2
s = mlab.mesh(x, y, z)
alpha = 30  # degrees
mlab.view(azimuth=0, elevation=90, roll=-90+alpha)

mlab.show()

or following @Tamas answer:

#parabaloid
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from math import sin, cos, pi
import matplotlib.cm as cm

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

#creating grid
y = np.linspace(-1,1,200)
x = np.linspace(-1,1,200)
x,y = np.meshgrid(x,y)

#set z values
z0 = x**2+y**2

# rotate the samples by pi / 4 radians around y
a = pi / 4
t = np.transpose(np.array([x,y,z0]), (1,2,0))
m = [[cos(a), 0, sin(a)],[0,1,0],[-sin(a), 0, cos(a)]]
x,y,z = np.transpose(np.dot(t, m), (2,0,1))
# or `np.dot(t, m)` instead `t @ m`


#label axes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

#plot figure
ax.plot_surface(x,y,z,linewidth=0, antialiased=False, shade = True, alpha = 0.5, facecolors=cm.viridis(z0))

plt.show()

Concoction

why use that (2,0,1) in line x,y,z = np.transpose(np.dot(t, m), (2,0,1)) – Alcoran

Answer 2

Something like this?

ax.view_init(-140, 30)

Insert it just before your plt.show() command.

Pangaro

Thanks for the response, however I need to rotate through multiple different degrees, not just 180. Also, I need to keep the viewing angle fixed. – Pinzler

@Dman - Not sure I fully understand, but every time you'll issue an ax.view_init command the axes will rotate. – Pangaro

maybe you can use mayavi there you can control the roll of the camera see: docs.enthought.com/mayavi/mayavi/auto/mlab_camera.html#roll – Concoction

How do I use that with my example? – Pinzler

You can refer to the documentation for meaning of the parameters. – Conurbation

Answer 3

The best I could come up with is to rotate the data itself.

#parabaloid
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from math import sin, cos, pi

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

#creating grid
y = np.linspace(-1,1,200)
x = np.linspace(-1,1,200)
x,y = np.meshgrid(x,y)

#set z values
z = x**2+y**2

# rotate the samples by pi / 4 radians around y
a = pi / 4
t = np.transpose(np.array([x,y,z]), (1,2,0))
m = [[cos(a), 0, sin(a)],[0,1,0],[-sin(a), 0, cos(a)]]
x,y,z = np.transpose(t @ m, (2,0,1))
# or `np.dot(t, m)` instead `t @ m`


#label axes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

#plot figure
ax.plot_surface(x,y,z,linewidth=0, antialiased=False, shade = True, alpha = 0.5)

plt.show()

Xeres

Thanks a lot. Could you also rotate the axis? I need to do this since the colors will be changed otherwise (the 'top' of my color map will be at the top now instead of at the bottom where the highest value of 'z' should be. – Pinzler

@No, with this method not. I dont know a way to rotate the axes. – Xeres

Do you have any suggestions on how to retain the colormap then? – Pinzler

Answer 4

I can't seem to add a comment just yet but I wanted to make an amendment to Tamas' implementation. There is an issue where the surface is not rotated counter-clockwise to the axis (the y-axis in this case) where the y-axis is coming out of the page. Rather, it's rotated clockwise.

In order to rectify this, and to make it more straightforward, I construct the x, y and z grids and reshape them into straightforward lists on which we perform the rotation. Then I reshape them into grids in order to use the plot_surface() function:

import numpy as np
from matplotlib import pyplot as plt
from math import sin, cos, pi
import matplotlib.cm as cm

num_steps = 50

# Creating grid
y = np.linspace(-1,1,num_steps)
x = np.linspace(-1,1,num_steps)
x,y = np.meshgrid(x,y)

# Set z values
z = x**2+y**2

# Work with lists
x = x.reshape((-1))
y = y.reshape((-1))
z = z.reshape((-1))

# Rotate the samples by pi / 4 radians around y
a = pi / 4
t = np.array([x, y, z])
m = [[cos(a), 0, sin(a)],[0,1,0],[-sin(a), 0, cos(a)]]
x, y, z = np.dot(m, t)

ax = plt.axes(projection='3d')

# Label axes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

# Plot the surface view it with y-axis coming out of the page. 
ax.view_init(30, 90)
    
# Plot the surface.
ax.plot_surface(x.reshape(num_steps,num_steps), y.reshape(num_steps,num_steps), z.reshape(num_steps,num_steps));

Cimbalom

Answer 5

here is the best solution: - First, you have to perform your python script in the Spyder environment which is easy to get by downloading Anaconda. Once you perform your script in Spyder, all you have to do is to follow the next instructions:

1. Click on “Tools”.
2. Click on “Preferences”.
3. Click on “IPython console”.
4. Click on “Graphics”.
5. Here you’ll find an option called “Backend”, you have to change it from “Inline” to “Automaticlly”.
6. Finally, apply the performed changes, then Click on “OK”, and reset spyder!!!!.

Once you perform the prior steps, in theory, if you run your script, then the graphics created will appear in a different windows and you could interact with them through zooming and panning. In the case of 3d plots (3d surface) you will be able to orbit it.

Shellback

this doesn't address the question. – Deign