Verlet simulation
Your best bet is verlet chain simulation. It incorporates gravity, constraints, and can have forces applied at any point.
In verlet integration (dividing the math into steps) you only store the vertice's current location and the location in the previous frame. Unlike euclidean integration in which you store the current position and the current speed and direction, verlet integration stores the current speed and direction as the difference between positions. This is very well suited to the type of simulation you are after where complex interaction do not have to bother with issues like momentum, rotation and a host of other problems. All you do is remember the last position and set the new, everything else happens automatically.
I will use javascript notation as I have never used actionscript.
The basics.
The sim starts with points (vertices). A vertex is a free point without size. It has forces of gravity applied per frame and it is constrained by environmental objects like the ground.
The information required to store a vertex
vertex = {
x : 100, // current position
y : 100,
lx : 100, // last position This point is not moving hence the last pos
ly : 100, // is the same as the current
}
For each frame of the animation you apply the various forces to the vertex
Move point function and some constants
GRAV = 0.9; // force of gravity
GROUND = 400; // Y position of the ground. Y is down the screen
GROUND_BOUNCE = 0.5; // Amount of bounce from the ground
DRAG = 0.9; // Amount of friction or drag to apply per frame
dx = (vertex.x-vertex.lx) * DRAG; // get the speed and direction as a vector
dy = (vertex.y-vertex.ly) * DRAG; // including drag
vertex.lx = vertex.x; // set the last position to the current
vertex.ly = vertex.y;
vertex.x += dx; // add the current movement
vertex.y += dy;
vertex.y += GRAV; // add the gravity
Each frame you also need to apply constraints. They can be almost anything.
For now this will just be the ground. If the position is greater than the ground line then move the point away from the ground. The point may also be fixed (not needing the above movement drag and gravity applied) or fixed to a moving object, like the mouse.
Constraining to the ground line.
Because the last position (vertex.lx, vertex.ly) helps define the current movement. When we change direction (hit the ground) we must change the last position to correctly describe the new direction, this puts the last position under the ground.
Constrain point function
if(vertex.y > GROUND){
// we need the current speed
dx = (vertex.x-vertex.lx) * DRAG;
dy = (vertex.y-vertex.ly) * DRAG;
speed = sqrt(dx*dx+dy*dy);
vertex.y = GROUND; // put the current y on the ground
vertex.ly = GROUND + dy * GROUND_BOUNCE; // set the last point into the
// ground and reduce the distance
// to account for bounce
vertex.lx += (dy / speed) * vx; // depending on the angle of contact
// reduce the change in x and set
// the new last x position
}
A bunch of points.
That is the basic math for gravity, air friction, and constraints, if we create a point and apply the math it will fall to the ground, bounce a few times and come to a stop.
Because we will need many vertices you create an array of them called for this answer points.
Now it is time to connect these points and turn a bunch of free floating vertices into a wide variety of simulated structures.
The line constraint
For this answer the line represents a link in the chain.
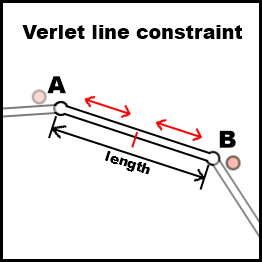
![enter image description here]()
The above image is to help visualise the concept. A and B are two vertices, the red dots next to them are the last position of the vertices. The red arrow show the approx direction that the vertices will be moved by the line constraint. The length of the line is fixed and the algorithm below attempts to find the best solution that keeps all the lines as close as possible to this length.
Describing a line
line = {
pointIndex1 : 0, // array index of connected point
pointIndex2 : 1, // array index of second connected point
length : 100, // the length of the line.
// in the demo below I also include a image index and
// a draw function
}
A line connects two vertices. A vertex can have many lines connected to it.
Each frame after we apply the movement, drag, gravity, and any other constraints we apply the line constraints. From the image above you can see that the last position of the two vertices were at positions that were too far apart for the line to connect. To fix the line we move both vertices equal amounts towards the center point of the line (red arrows). If the two points were too close for the line length we would move the points apart.
The following is the math used to do this.
Constrain line function
p1 = points[line.pointIndex1]; // get first point
p2 = points[line.pointIndex2]; // get second point
// get the distance between the points
dx = p2.x - p1.x;
dy = p2.y - p1.y;
distance = sqrt(dx * dx + dy * dy);
// get the fractional distance the points need to move toward or away from center of
// line to make line length correct
fraction = ((line.length - distance) / distance) / 2; // divide by 2 as each point moves half the distance to
// correct the line length
dx *= fraction; // convert that fraction to actual amount of movement needed
dy *= fraction;
p1.x -=dx; // move first point to the position to correct the line length
p1.y -=dy;
p2.x +=dx; // move the second point in the opposite direction to do the same.
p2.y +=dy;
This constraint is very simple and because we are using verlet integration we don't have to worry about the speed and direction of the points, or of the line. Best of all we don't have to deal with any rotation as that is taken care of as well.
Many points, many lines
At this point we have done all the math needed for a single line, we can add more lines, connecting the end point of the first line to the start of the second line and so on, however long we need the chain. Once we have all the points connected we apply the standard constraints to all the points and then apply the line constraints one by one.
This is where we run into a small problem. When we move the points to correct the length of the first line we move the start point of the next line, then when we move the points for the next line we move the endpoint of the first line breaking its length constraint. When we have gone through all the lines the only line that will have the correct length will be the last one. All the other lines will be pulled slightly toward the last line.
We could leave it as is and that would give the chain a somewhat elastic feel (undesirable in this case but for whips and ropes it works great), we could do a full inverse kinematics end point solution for the line segments (way to hard) or we can cheat. If you apply the line constraint again you move all the points a little more towards the correct solution. We do this again and again, correcting a little for the error introduced in the every previous pass.
This iterative process will move towards a solution but it will never be a perfect, yet we can quickly get to a situation where the error is visually unnoticeable. For convenience I like to call the number of iteration the stiffness of the sim. A value of 1 means the lines are elastic, a value of 10 means there is almost no noticeable stretching of the lines.
Note that the longer the chain the more noticeable the stretching becomes and thus the more iterations need to be done to get the required stiffness.
Note this method of finding a solution has a flaw. There are many cases where there is more than one solution to the arrangement of points and lines. If there is a lot of movement in the system it may start oscillating between the two (or more) possible solutions. If this happens you should limit the amount of movement a user can add to the system.
The Main loop.
Putting that all together we need to run the sim once every frame. We have an array of points, and an array of lines connecting the points. We move all the points, then we apply the line constraints. Then render the result ready to do all again next frame.
STIFFNESS = 10; // how much the lines resist stretching
points.forEach(point => { // for each point in the sim
move(point); // add gravity drag
constrainGround(point); // stop it from going through the ground line
})
for(i = 0; i < STIFFNESS; i+= 1){ // number of times to apply line constraint
lines.forEach(line => { // for each line in the sim
constrainLine(line);
})
}
drawPoints(); // draw all the points
drawLines(); // draw all the lines.
Question specific issues
The above method provides a great line simulation, It also does rigid bodies, rag dolls, bridges, boxes, cows, goats, cats, and dogs. By fixing points you can do a variety of hanging ropes and chains, create pulleys, tank tread. Great for simulating 2D cars and bikes. But remember they are all visually acceptable but are not at all a real physics simulation.
You want a chain. To make a chain we need to give the lines some width. So each vertex needs a radius, and the ground constraint needs to take that into account. We also want the chain to not fall in on itself so we need a new constraint that prevents balls (AKA vertices) from overlapping each other. This will add quite an extra load to the sim as each ball needs to be tested against each other ball, and as we adjust the position to stop overlap we add error to the line lengths so we need to do each constraint in turn many times to get a good solution per frame.
And the final part is the details of the graphics, Each line needs to have a reference to a image that is a visual representation of the chain.
I will leave all that up to you to work out how best to do in actionscript.
A demo
The following demo shows the result of all the above. It may not be what you want, and there are other ways to solve the problem. This method has several problems
- Discrete mass, the mass is defined by points, you cant make points lighter or heavier without a lot more math
- Oscillating state. Sometimes the system just starts to oscillate, try to keep movement within a reasonable level.
- Stretching. Though stretching can be almost eliminated there are some situations that the solution will not be perfect. Like an elastic band if a stretch chain is released it will flick. I have not increased the iteration count to match the chain length so the longer chains will show stretching and if you swing it about you will see the chain separate.
The functions you will be interested in are constrainPoint, constrainLine, movePoint, and doSim (just the bit after if(points.length > 0){ in runSim) all the rest is just support and boilerplate.
Best viewed as full page (I made the images a little too big oops... :(
To see the chain click and hold right mouse button to add first block then adds links to the chain. I have not set a limit to the length of the chain. Click and hold the left button to grab and drag any part of the chain and block.
var points = [];
var lines = [];
var pointsStart;
var fric = 0.999; // drag or air friction
var surF = 0.999; // ground and box friction
var grav = 0.9; // gravity
var ballRad = 10; // chain radius set as ball radius
var stiffness = 12; // number of itterations for line constraint
const fontSize = 33;
var chainImages = [new Image(),new Image(),new Image()];
chainImages[0].src = "https://i.sstatic.net/m0xqQ.png";
chainImages[1].src = "https://i.sstatic.net/fv77t.png";
chainImages[2].src = "https://i.sstatic.net/tVSqL.png";
// add a point
function addPoint(x,y,vx,vy,rad = 10,fixed = false){
points.push({
x:x,
y:y,
ox:x-vx,
oy:y-vy,
fixed : fixed,
radius : rad,
})
return points[points.length-1];
}
// add a constrained line
function addLine(p1,p2,image){
lines.push({
p1,p2,image,
len : Math.hypot(p1.x - p2.x,p1.y-p2.y),
draw(){
if(this.image !== undefined){
var img = chainImages[this.image];
var xdx = this.p2.x - this.p1.x;
var xdy = this.p2.y - this.p1.y;
var len = Math.hypot(xdx,xdy);
xdx /= len;
xdy /= len;
if(this.image === 2){ // oops block drawn in wrong direction. Fix just rotate here
// also did not like the placement of
// the block so this line's image
// is centered on the lines endpoint
ctx.setTransform(xdx,xdy,-xdy,xdx,this.p2.x, this.p2.y);
ctx.rotate(-Math.PI /2);
}else{
ctx.setTransform(xdx,xdy,-xdy,xdx,(this.p1.x + this.p2.x)/2,(this.p1.y + this.p2.y)/2);
}
ctx.drawImage(img,-img.width /2,- img.height / 2);
}
}
})
return lines[lines.length-1];
}
// Constrain a point to the edge of the canvas
function constrainPoint(p){
if(p.fixed){
return;
}
var vx = (p.x - p.ox) * fric;
var vy = (p.y - p.oy) * fric;
var len = Math.hypot(vx,vy);
var r = p.radius;
if(p.y <= r){
p.y = r;
p.oy = r + vy * surF;
}
if(p.y >= h - r){
var c = vy / len
p.y = h - r
p.oy = h - r + vy * surF;
p.ox += c * vx;
}
if(p.x < r){
p.x = r;
p.ox = r + vx * surF;
}
if(p.x > w - r){
p.x = w - r;
p.ox = w - r + vx * surF;
}
}
// move a point
function movePoint(p){
if(p.fixed){
return;
}
var vx = (p.x - p.ox) * fric;
var vy = (p.y - p.oy) * fric;
p.ox = p.x;
p.oy = p.y;
p.x += vx;
p.y += vy;
p.y += grav;
}
// move a line's end points constrain the points to the lines length
function constrainLine(l){
var dx = l.p2.x - l.p1.x;
var dy = l.p2.y - l.p1.y;
var ll = Math.hypot(dx,dy);
var fr = ((l.len - ll) / ll) / 2;
dx *= fr;
dy *= fr;
if(l.p2.fixed){
if(!l.p1.fixed){
l.p1.x -=dx * 2;
l.p1.y -=dy * 2;
}
}else if(l.p1.fixed){
if(!l.p2.fixed){
l.p2.x +=dx * 2;
l.p2.y +=dy * 2;
}
}else{
l.p1.x -=dx;
l.p1.y -=dy;
l.p2.x +=dx;
l.p2.y +=dy;
}
}
// locate the poitn closest to x,y (used for editing)
function closestPoint(x,y){
var min = 40;
var index = -2;
for(var i = 0; i < points.length; i ++){
var p = points[i];
var dist = Math.hypot(p.x-x,p.y-y);
p.mouseDist = dist;
if(dist < min){
min = dist;
index = i;
}
}
return index;
}
function constrainPoints(){
for(var i = 0; i < points.length; i ++){
constrainPoint(points[i]);
}
}
function movePoints(){
for(var i = 0; i < points.length; i ++){
movePoint(points[i]);
}
}
function constrainLines(){
for(var i = 0; i < lines.length; i ++){
constrainLine(lines[i]);
}
}
function drawLines(){
// draw back images first
for(var i = 0; i < lines.length; i ++){
if(lines[i].image !== 1){
lines[i].draw();
}
}
for(var i = 0; i < lines.length; i ++){
if(lines[i].image === 1){
lines[i].draw();
}
}
}
// Adds the block at end of chain
function createBlock(x,y){
var i = chainImages[2];
var w = i.width;
var h = i.height;
var p1 = addPoint(x,y+16,0,0,8);
var p2 = addPoint(x-w/2,y+27,0,0,1);
var p3 = addPoint(x+w/2,y+27,0,0,1);
var p4 = addPoint(x+w/2,y+h,0,0,1);
var p5 = addPoint(x-w/2,y+h,0,0,1);
var p6 = addPoint(x,y+h/2,0,0,1);
addLine(p1,p2);
addLine(p1,p3);
addLine(p1,p4);
addLine(p1,p5);
addLine(p1,p6,2);
addLine(p2,p3);
addLine(p2,p4);
addLine(p2,p5);
addLine(p2,p6);
addLine(p3,p4);
addLine(p3,p5);
addLine(p3,p6);
addLine(p4,p5);
addLine(p4,p6);
addLine(p5,p6);
var p7 = addPoint(x,y + 16-(chainImages[0].width-ballRad * 2),0,0,ballRad);
addLine(p1,p7,1);
}
var lastChainLink = 0;
function addChainLink(){
var lp = points[points.length-1];
addPoint(lp.x,lp.y-(chainImages[0].width-ballRad*2),0,0,ballRad);
addLine(points[points.length-2],points[points.length-1],lastChainLink % 2);
lastChainLink += 1;
}
function loading(){
ctx.setTransform(1,0,0,1,0,0)
ctx.clearRect(0,0,w,h);
ctx.fillStyle = "black";
ctx.fillText("Loading media pleaase wait!!",w/2,30);
if(chainImages.every(image=>image.complete)){
doSim = runSim;
}
}
var onResize = function(){ // called from boilerplate
blockAttached = false;
lines.length = 0; // remove all lines and points.
points.length = 0;
lastChainLink = 0; // controls which chain image to use next
holdingCount = 0;
holding = -1;
mouse.buttonRaw = 0;
}
var blockAttached = false;
var linkAddSpeed = 20;
var linkAddCount = 0;
var holding = -1; // the index of the link the mouse has grabbed
var holdingCount = 0;
function runSim(){
ctx.setTransform(1,0,0,1,0,0)
ctx.clearRect(0,0,w,h);
ctx.fillStyle = "black";
if(points.length < 12){
ctx.fillText("Right mouse button click hold to add chain.",w/2,30);
}
if(holdingCount < 180){
if(mouse.buttonRaw & 1 && holding === -2){
ctx.fillText("Nothing to grab here.",w/2,66);
}else{
ctx.fillText("Left mouse button to grab and move chain.",w/2,66);
}
}
if(mouse.buttonRaw & 4){
if(linkAddCount > 0){ // delay adding links
linkAddCount-=1;
}else{
if(!blockAttached ){
createBlock(mouse.x,mouse.y)
blockAttached = true;
}else{
addChainLink(mouse.x,mouse.y);
}
linkAddCount = linkAddSpeed;
}
}
if(points.length > 0){
if(mouse.buttonRaw & 1){
if(holding < 0){
holding = closestPoint(mouse.x,mouse.y);
}
}else{
holding = -1;
}
movePoints();
constrainPoints();
// attach the last link to the mouse
if(holding > -1){
var mousehold = points[holding];
mousehold.ox = mousehold.x = mouse.x;
mousehold.oy = mousehold.y = mouse.y;
holdingCount += 1; // used to hide help;
}
for(var i = 0; i < stiffness; i++){
constrainLines();
if(holding > -1){
mousehold.ox = mousehold.x = mouse.x;
mousehold.oy = mousehold.y = mouse.y;
}
}
drawLines();
}else{
holding = -1;
}
}
var doSim = loading;
/*********************************************************************************************/
/* Boilerplate not part of answer from here down */
/*********************************************************************************************/
var w, h, cw, ch, canvas, ctx, mouse, globalTime = 0, firstRun = true;
function start(x,y,col,w){ctx.lineWidth = w;ctx.strokeStyle = col;ctx.beginPath();ctx.moveTo(x,y)}
function line(x,y){ctx.lineTo(x,y)}
function end(){ctx.stroke()}
function drawLine(l) {ctx.lineWidth = 1;ctx.strokeStyle = "Black";ctx.beginPath();ctx.moveTo(l.p1.x,l.p1.y);ctx.lineTo(l.p2.x,l.p2.y); ctx.stroke();}
function drawPoint(p,col = "black", size = 3){ctx.fillStyle = col;ctx.beginPath();ctx.arc(p.x,p.y,size,0,Math.PI * 2);ctx.fill();}
;(function(){
const RESIZE_DEBOUNCE_TIME = 100;
var createCanvas, resizeCanvas, setGlobals, resizeCount = 0;
createCanvas = function () {
var c, cs;
cs = (c = document.createElement("canvas")).style;
cs.position = "absolute";
cs.top = cs.left = "0px";
cs.zIndex = 1000;
document.body.appendChild(c);
return c;
}
resizeCanvas = function () {
if (canvas === undefined) {
canvas = createCanvas();
}
canvas.width = innerWidth;
canvas.height = innerHeight;
ctx = canvas.getContext("2d");
if (typeof setGlobals === "function") {
setGlobals();
}
if (typeof onResize === "function") {
if(firstRun){
onResize();
firstRun = false;
}else{
resizeCount += 1;
setTimeout(debounceResize, RESIZE_DEBOUNCE_TIME);
}
}
}
function debounceResize() {
resizeCount -= 1;
if (resizeCount <= 0) {
onResize();
}
}
setGlobals = function () {
cw = (w = canvas.width) / 2;
ch = (h = canvas.height) / 2;
ctx.font = fontSize + "px arial";
ctx.textAlign = "center";
ctx.textBaseline = "middle";
}
mouse = (function () {
function preventDefault(e) {
e.preventDefault();
}
var mouse = {
x : 0,
y : 0,
w : 0,
buttonRaw : 0,
over : false,
bm : [1, 2, 4, 6, 5, 3],
active : false,
bounds : null,
mouseEvents : "mousemove,mousedown,mouseup,mouseout,mouseover,mousewheel,DOMMouseScroll".split(",")
};
var m = mouse;
function mouseMove(e) {
var t = e.type;
m.bounds = m.element.getBoundingClientRect();
m.x = e.pageX - m.bounds.left;
m.y = e.pageY - m.bounds.top;
if (t === "mousedown") {
m.buttonRaw |= m.bm[e.which - 1];
} else if (t === "mouseup") {
m.buttonRaw &= m.bm[e.which + 2];
} else if (t === "mouseout") {
m.buttonRaw = 0;
m.over = false;
} else if (t === "mouseover") {
m.over = true;
} else if (t === "mousewheel") {
m.w = e.wheelDelta;
} else if (t === "DOMMouseScroll") {
m.w = -e.detail;
}
e.preventDefault();
}
m.start = function (element) {
m.element = element === undefined ? document : element;
m.mouseEvents.forEach(n => {
m.element.addEventListener(n, mouseMove);
});
m.element.addEventListener("contextmenu", preventDefault, false);
m.active = true;
}
return mouse;
})();
function update(timer) { // Main update loop
doSim(); // call demo code
requestAnimationFrame(update);
}
setTimeout(function(){
resizeCanvas();
mouse.start(canvas, true);
window.addEventListener("resize", resizeCanvas);
requestAnimationFrame(update);
},0);
})();
Images used in demo
![enter image description here]()
![enter image description here]()
![enter image description here]()