Data structure to search name of files and get its path

Question

I will be inserting names of files in a dynamically way, approximately till 1 billion of names. Besides, I do also want to store the path where the files are located in order to do the following queries:

• Searching wheter the name of a file is stored in order to get its path.
• Searching the name of all the files which matches with a substring, a kinda of a like-query (e.g. If a search *o*, it will return me joel, hola, ola, oso, osea, algo, if a search aa*, it will return me aaab and if I search *so, It will return oso).
• Delete the name of a file.

So, I am trying to make a kind of trie data structure in the following way:

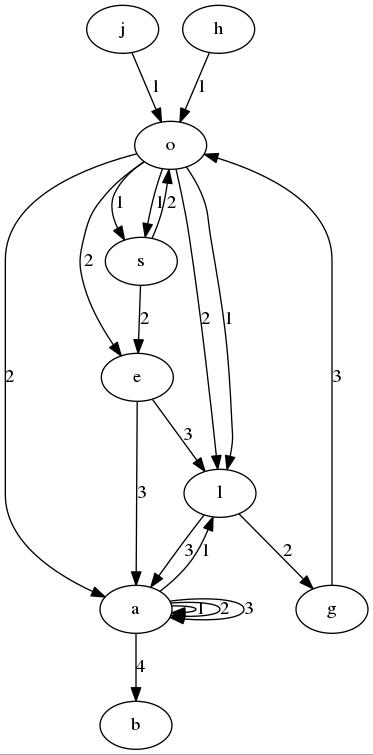
I got 26 nodes (the english alphabet a-z, I am not going to put all the nodes in the image because space) such that if I insert the word "hola" then I create an edge from node with the letter 'h' to node with the letter 'o' and whose edge has a data 1 since this number represent the level of the depth. Furthermore, in the node where 'a' is stored, I will have a map structure in order to store the path of the file, this is because I will surely have a lot of paths stored in the node which contains the letter 'a'.

Having said that, I inserted the following words: joel, hola, ola, oso, osea, algo, aaab.

I have done so because I do not want to have many nodes with the sama lettres (e.g. a, b, etc) but the problem is that I got a lot of edges and the sctructure needs

bytes of memory (I am programming in C++) where w is a string of size .

As you can see, if I search for the name of file "jola" (which is not inserted) no path will returned and this tell us that such file is not stored.

How can I improve this? Is it any way to reduce the number of edges? or there exists a better structure and way to do this? I am very open to hear of any suggestion.

Jester

For more memory savings, consider a Directed Acyclic Word Graph (DAWG). en.wikipedia.org/wiki/… Typically, you build a trie and then optimize it. – Tobar

What is the purpose of the data structure? what problem is it meant to solve? – Dramatic

Dear @Amit, the purpose is inserting in a dynamically way and searching a word. The problem is the structure has many edges with data of the level that would be expensive in the time. – Jester

I'm pretty sure your diagram is incorrect for your example (for example, why is -> b = 4 ??). Also, this data structure doesn't support the use case you describe - how will it indicate that "jola" is not a word? – Dramatic

Dear @Amit, thank you for your comment. Clearly you are right, but when I insert a string, by example hola, in the node which contains 'a' I write a 'path' (e.g. /home/user/hola)' which means hola is in this path. As I have not inserted jola, it will not return me any path. Sorry for omitting this explanation in the question – Jester

So in the end you'll have a list of all "paths" that end with the letter stored in a single collection attached to that letter's node? Sounds like you gain nothing by building this data structure - to validate a match you'll have to iterate the collection (hopefully it will be maintained sorted and you could binary search), and for non matches you'll still have a good chance of hitting a false end node. Not trying to be negative, but this looks less & less effective - sorry. – Dramatic

When you say "substring", do you mean "prefix"? If so, then a trie (optimized) is a good data structure as @Jim Mischel commented. – Vaudois

Dear @mikep, thank you for your comment. I already clarified the examples in the question. If it is so, please explain your answer in more detail, I already trying a kind of a trie, but I think it is not optimized. – Jester

I really think you're looking for a directed acyclic word graph (DAWG), which is a highly optimized trie. The idea is that you build a normal trie and then apply some well-known optimizations. I've seen this used to encode a 650,000 word English dictionary in about a megabyte of memory. – Tobar

Do you actually have about a billion of different names? or do the names repeat? – Pomace

@StefanHaustein They are all different. – Jester

May fzf codebase give some inspiration? – Proponent

Here is a link to directed acyclic word graph, that mentioned JohnPaul Adamovsky's Implementation in C. – Noleta

Answer 1

I have solved a somewhat similar problem in the past, for storing wordlists for crossword puzzles, and finding words very fast. I called it a "superindex". My main goal was speed, not storage size, but the original question does not state what the author considers as an "improvement": maybe it is size, maybe it is speed, maybe it is algorithm complexity. My approach yielded tremendous speed at relatively small complexity, but with rather moderate savings in storage size. The approach was as follows:

1. Use a tree, not a graph. Each node in the tree has up to 26 "entries". Each entry stands for a letter of the alphabet and contains a link to a child node, or, if the entry belongs to a leaf node, then a link to the "payload", which in your case is a "path". So, when a node contains an entry for a given letter, this signifies that there exists a "name" with that letter in that position. (The position being the depth of the node in the tree.)

2. Separate all names by name-length, because that's very easy to determine. Use an entirely separate tree for each name-length. This means that in each tree all leaf nodes are at exactly the same depth, and the only nodes in the tree that contain additional data (a path in your case) are the leaf nodes. This keeps things very simple.

So, the search algorithm is as follows:

1. Among all different trees for different name lengths, use the one which corresponds to the length of the "name" you are searching for.
2. Begin with the first letter of the "name" you are looking for, and at the root node of the tree.
3. Find the entry for the current letter in the current node; if no such entry exists, then the name was not found, done. Otherwise:
4. If we have reached a leaf node, then the name has been found, return the payload, which in your case is a "path". Otherwise:
5. Move on to the next letter of the word you are looking for; follow the link from the found entry in the current node to the next child node; go to step 3.

As you can see, this is a fairly simple algorithm, and it is guaranteed to be very fast. Without any further optimizations, the storage requirements will be of the order of one "entry" per name stored, and an "entry" will consist of a character plus a pointer.

Then, there is a multitude of optimizations possible. For example, an "entry", might be useful concept when reasoning about your data structure, but it can be completely annihilated in the actual implementation: in each node you can have a single "summary" 32-bit machine word where each of the first 26 bits indicates whether the corresponding letter of the alphabet is present or not in the node, followed by an array of pointers to child nodes (or payloads) which contains as many elements as there are set bits in the summary word.

Mesocratic