3D collision detection : convex hull vs convex hull , need Position and Normal

Question

I want to know an approximate 3D position and 3D normal of collision site between two 3D convex hulls (A vs B).

The CPU in parenthesis shows relative CPU-time needed in my finished program.

Part 1: Early-out (CPU 1%)

In the first step, I use a very cheap algorithm - separation axis theorem.
For example, I use 15 axis for 2 cubes. (In real cases, the shapes are more complex.)
If there is at least 1 axis that can separate, return "no-collide".
Otherwise, do the next part.

Part 2: Vertex vs Volume (CPU 10%)

• Check every vertices of A - whether it is inside B.
• Check every vertices of B - whether it is inside A.

Part 3: Edge vs Edge (CPU >20%)

There is a strange case e.g. https://gamedev.stackexchange.com/questions/75437/collision-detection-3d-rectangles-using-sat . I stole the image from there:-

Thus, I also need edge vs edge.

• For every pair of A & B edges (12 * 12 = 144 pairs), find a nearest point in edge of A against the edge of B. Check whether the vertex is inside B.
• (vice versa) For every pair of B & A edges, check whether such vertex is inside A.

Wow, that is a lot of computation.
However, it is not over yet.

Problem

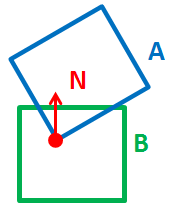
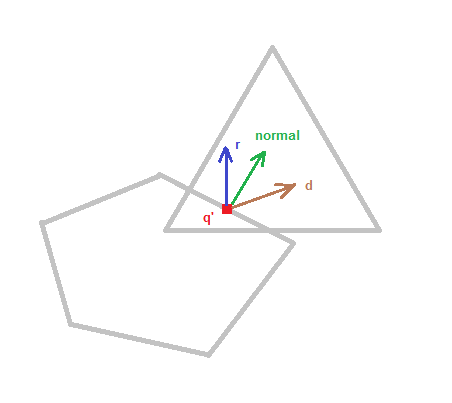
1. The reported collision position is not so accurate (left:current , right:wish) :-

   To solve it, I thought about generating a new convex shape = A intersect B.
   There are some C++ free libraries out there (e.g. OpenMesh), but I think it is too CPU-expensive.
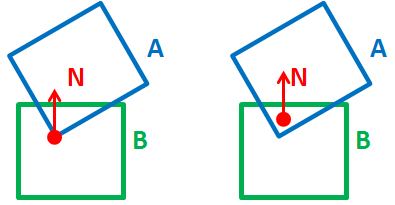
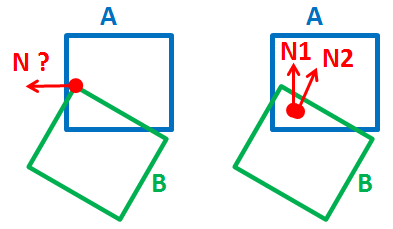
   Note that I don't need it to be precisely correct.

2. It also sometimes reports wrong normal (left:current , right:wish) :-

   ^ This problem might be solved by adding edge (of A) vs face (of B) check, but that would make the whole collision detection even more expensive.

Question

It looks like common algorithms in the internet (from which I copy) recognizes only micro feature.
IMHO, the vertex-volume/edge-edge algorithm focus on topology rather that the fact that both shapes are solid volumes.

What is the algorithm that is more accurate (1st priority) and perhaps cheaper?
My approach might be wrong at the foundation level.

To speed things up, I already did some pruning e.g. select only pair of edge A & B that is close together.

References :-

• Algorithms for Collision Detection between Arbitrarily sized Convex Polygons checks only whether collision occurs.

• https://pybullet.org/Bullet/BulletFull/btBoxBoxDetector_8cpp_source.html : inspiring full code of box vs box collision detection in Bullet Physics library - it is hard to understand.

• https://math.stackexchange.com/questions/397413/determine-direction-of-minimum-overlap-of-convex-polygons Unanswered Math question that is very similar to this.

Edit (10 days later)

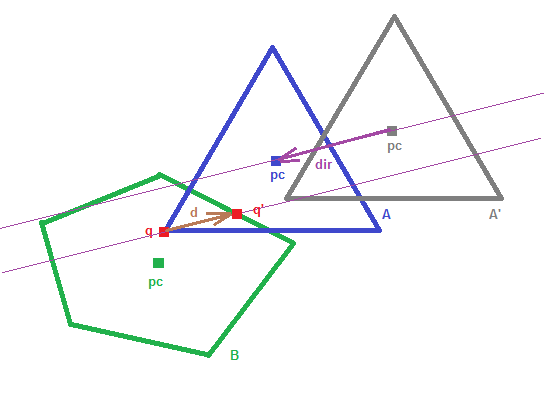
Now, I can find all intersecting convex point (the convex is depicted as a pink triangle/rectangle) :-

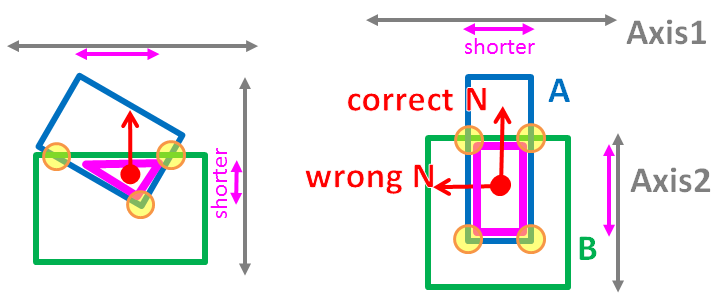
Here is how I find the normal.

For-each separating axis (all=15 axis), I project the pink convex on to the axis.
The axis that yields the shortest projection distance (pink arrow) should be the direction of normal.

My above assumption is often correct (e.g. left), but sometimes wrong (e.g. right).
How to improve it CPU-cheaply?

Donniedonnish

Is this homework? – Katiekatina

@Willem Van Onsem Ha ha. No, it is a part of my ECS game engine. I am crazy enough to create my own Physics Engine too (Bullet is not suitable for me). – Donniedonnish

In your first current vs wish image, I don't understand what is the problem? Why the image on the left shows "wrong" but the image on the right shows "correct" collision point?. About part 3, If you follow the link you gave, an answer explains SAT is enough to detect the collision but you need to test 15 axes, not just 6 normal axes. gamedev.stackexchange.com/questions/44500/…. But you need more work to detect your desired contact point. – Subacid

@Subacid It is not so correct because the reported collision point should be around center of the overlapping zone. IMHO, a point that is near the overlapping boundary is not a so good representative for the collision event. About part 3, do you mean that I can extend the 15 axes SAT to find the contact position? – Donniedonnish

Have you considered going for exact collition point and time? You would need something like kinematic datastructures to track it happening, but it would make the determination of face and point much simpler when you have detected collition. You could also try to reverse the move and track the original point of collition. This would change the problem though. – Carabineer

@Carabineer Thank. I am new to this. What is the technique/approach name (so I can read more)? – Donniedonnish

What I mean is, SAT with 15 axes is enough to know whether a collision has happened or not, you do not need any special work to detect edge-edge collisions. If you look at the bullet source code, they do 15 tests. If the collision is an edge-edge collision ( if (code > 6) part ), they calculate contact points easier compared to non-edge collisions (rest of the function). I do not know the details of what they do to obtain contact points of non-edge collisions, but I am sure you can follow it given the code is well commented. – Subacid

@Subacid Cool, thank. I can't find any reference/theory about it (15 axes = no longer need edge-edge detection), but from your comment + various diagrams, now I feel/believe that it is true. Thank for confirming this. XD – Donniedonnish

You can look up kinetic data structures, Here is a link to a introduction to one: link. They are used for tracking things that changes structure over time (such as the convex hull of a set of moving points or which way objects move when they might collide). Reading about them should give you some nice abstraction to think about when you make your engine. It is generally harder to solve a problem with genetic data structures, but their solutions may have some significant advantages (here that you get exact time). – Carabineer

@Carabineer Whoa, that is a new universe for me ; kinda look like an advance kind of continuous collision detection. Thank. – Donniedonnish

If you have arbitrary convex hulls, then GJK algorithm might be handy for collision detection. As for penetration distance, I think computing it exactly is hardly feasible, so heuristics should be used. – Endurable

@stagtilov Thank. It is useful. Personally, I don't appreciate Simplex much because it is hard to make it (numerical) stable. E.g. mosh's C++ code in #3957450, but it gives wrong result of test case for me (coliru.stacked-crooked.com/a/5b750c415321058a). – Donniedonnish

Answer 1

Game engines typically simulate time a series of discrete steps. As a consequence, the collision system can get into difficult (computationally expensive) cases due to interpenetration (your case) or when things are moving fast -tunneling where A is on one side of B at step N and entirely on the other side of B at step N+1. It is even harder if you need to deal with multibody contact or continuous contact or non convex or jointed or soft object. Yikes! we are simulating the whole world.

You want to do "game physics" and use approximations to buy back frame rate... In the end, you can cover a lot of error with a bunch of smoke puffs or light flares. :-)

There is a class of algorithms which explicitly take simulated time into account to help the collision system. There are a lot of ways to implement a "continuous collision detection" system. You can start here, but you should read widely first, before you commit to code. Fortunately, there is a lot of literature on collision. here is a good place to start https://docs.unity3d.com/Manual/ContinuousCollisionDetection.html https://pybullet.org/Bullet/phpBB3/viewtopic.php?t=20

Here is one suggested heuristic that might work in your existing system.... This heuristic technique might work in a game like astroids 3d where objects float in freely in space. That might be good enough for what you need.

Image every object stores its current state vector (position, orientation, velocity, acceleration, rotation... ) and its previous state vector from the previous time step.

Suppose you detected a potential collision between objects A and B at time=current.

For time=previous, assume A and B are not in contact.

Compute the closest points on the surfaces of A and B, respectively at time=prev using the previous state vectors of A and B. (closestA, closestB).

The line segment (closestA,closestB) will have non-zero length at time=previous. You could just use closestB for your position and normal, but it would have some error proportional to the length of the line segment..

So do a binary search in time, and minimize the error, by finding the time when A is arbitrarily close to B . At each pass of your search, cut search time step size in half. 0.5, 0.25, 0.125.. until the length of (closestA, closestB) is below an error threshold or you give up.

That should give you an acceptable approximate solution for the simple cases...

Also, you said you are using the separation axis theorem as your "first check". That actually sounds expensive to me if that is really the "first check"..

The fastest computation is the one you do not do, so fast collision means lots of cheap pretesting and avoiding the expensive cases.

You can consider using spatial techniques like a coarse spatial grid and only check objects which you already know are near each other.

Also, the sphere-sphere test is a very fast pretest to see if the bounding sphere of two convex object are even overlapping.

Proofread

Neutral comment : I already did AABB and boardphase, and I don't mind tunneling. I gave up the Binary Search, because it is very slow. It looks cool anyway. – Donniedonnish

yeah there is often a trade off between accuracy and speed. In practice its ok to have expensive branches in your code if they happen rarely "enough" for your situation. It's useful to implement the simplest thing first, that you can get away with, and add a comment "// OPTIMIZEME" and maybe you come back to it, maybe you never need to... – Proofread

Answer 2

I would do this:

1. definitions

   let have 2 triangulated 3D convex hulls A,B. Each of them has defined a center pc and list of surface points p0,p1,p2,... and list of triangles t0,t1,t2,.... Each triangle should have also computed its normal n0,n1,n2,... pointing out.

2. compute most inside hit point q

   so let test if A hits B. simply loop through all points A.p[i] and remember the inner most point that is inside B and closest to B.pc (if more than one). This assumes your simulation has small enough time step dt so interpolated positions do not miss hits ... If not the case another approach must be used.

3. compute displacement d

   for that we need to know direction of movement A relative to B. that can be computed like this:

   dir = (A.pc-B.pc) - (A'.pc-B'.pc)
   

   where A'.pc,B'.pc are positions from last iteration ... Here an image in relative therms (as B would stand still):

   now to compute displacement just cast a ray from q with direction -dir and test which triangle of B is hit. The intersection point q' is your hit point you looking for. The displacement:

    d = q'-q
   

   is what you need to translate A in order to just touch B instead of intersect.

   From this you can compute reflection r as the hit triangle of B has its own normal:

   so now just translate A by r so your A will have the position after reflection (so time is not lost during impact)... Also from the d size and relative speed between A,B you can estimate the time of impact and add the impact friction by scaling down speed and the r. Do not forget to reflect also speed of A. You can also do the impact physics on B.

   The q' and d can be also used to create a rotation torque on both A,B however simulating 3D rotations is very hard and usually is just faked by Euler angles... My understanding is that rigid body can have any number of rotations not just 3... but some of them combines or cancels out so in order to simulate that one would need to have a dynamic list of the rotations involved which would be slow and hard to implement stuff on top of it.

Take a look at:

• Cone to box collision

You can find my implementation of point inside convex_mesh test and much more there even AABB,OBB... In newer version of that I got even more primitives and convex_hull implemented but can't post it as it grow to 35 KByte which is pass the 30 KByte limit already.

To speed up the testing you can also add outscribed sphere to each convex_hull and test if they intersect before testing the convex_hull itself... You know perpendicular distance between the linear paths of A,B must be smaller than A.r+B.r ... colapsing to simple line/line closest point test which is also implemented in the link above.

Percentage