Good day SO community,
I am a CS student currently performing an experiment combining MergeSort and InsertionSort. It is understood that for a certain threshold, S, InsertionSort will have a quicker execution time than MergeSort. Hence, by merging both sorting algorithms, the total runtime will be optimized.
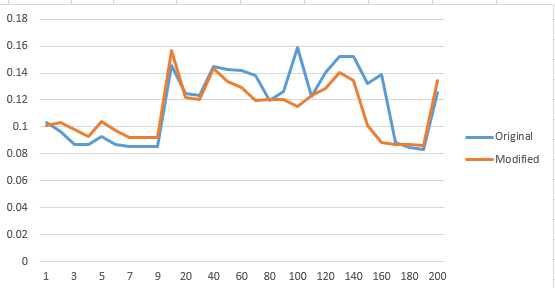
However, after running the experiment many times, using a sample size of 1000, and varying sizes of S, the results of the experiment does not give a definitive answer each time. Here is a picture of the better results obtained (Note that half of the time the result is not as definitive):
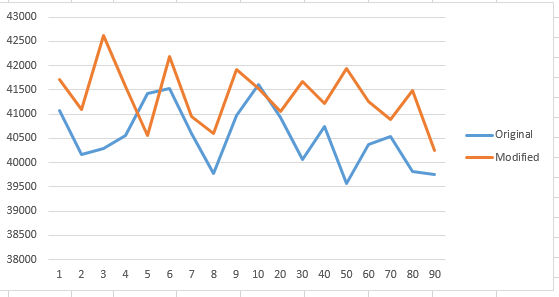
Now, trying the same algorithm code with a sample size of 3500:
Finally, trying the same algorithm code with a sample size of 500,000 (Note that the y-axis is in milliseconds:
Although logically, the Hybrid MergeSort will be faster when S<=10, as InsertionSort does not have recursive overhead time. However, the results of my mini experiment says otherwise.
Currently, these are the Time Complexities taught to me:
MergeSort: O(n log n)
InsertionSort:
- Best Case: θ(n)
- Worst Case: θ(n^2)
Finally, I have found an online source: https://cs.stackexchange.com/questions/68179/combining-merge-sort-and-insertion-sort that states that:
Hybrid MergeInsertionSort:
- Best Case: θ(n + n log (n/x))
- Worst Case: θ(nx + n log (n/x))
I would like to ask if there are results in the CS community that shows definitive proof that a Hybrid MergeSort algorithm will work better than a normal MergeSort algorithm below a certain threshold, S, and if so, why?
Thank you so much SO community, it might be a trivial question, but it really will clarify many questions that I currently have regarding Time Complexities and stuff :)
Note: I am using Java for the coding of the algorithm, and runtime could be affected by the way java stores data in memory..
Code in Java:
public static int mergeSort2(int n, int m, int s, int[] arr){
int mid = (n+m)/2, right=0, left=0;
if(m-n<=s)
return insertSort(arr,n,m);
else
{
right = mergeSort2(n, mid,s, arr);
left = mergeSort2(mid+1,m,s, arr);
return right+left+merge(n,m,s,arr);
}
}
public static int insertSort(int[] arr, int n, int m){
int temp, comp=0;
for(int i=n+1; i<= m; i++){
for(int j=i; j>n; j--){
comp++;
comparison2++;
if(arr[j]<arr[j-1]){
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
else
break;
}
}
return comp;
}
public static void shiftArr(int start, int m, int[] arr){
for(int i=m; i>start; i--)
arr[i] = arr[i-1];
}
public static int merge(int n, int m, int s, int[] arr){
int comp=0;
if(m-n<=s)
return 0;
int mid = (n+m)/2;
int temp, i=n, j=mid+1;
while(i<=mid && j<=m)
{
comp++;
comparison2++;
if(arr[i] >= arr[j])
{
if(i==mid++&&j==m && (arr[i]==arr[j]))
break;
temp = arr[j];
shiftArr(i,j++,arr);
arr[i] = temp;
if(arr[i+1]==arr[i]){
i++;
}
}
i++;
}
return comp;
}