Butterfly pattern appears in random walk using srand(), why?

Question

About 3 years ago I coded a 2D random walk togheter with a coleague in C++, first it seemed to work properly as we obtained a diferent pattern each time. But whenever we decided to increase the number of steps above some threshold an apparent butterfly pattern appeared, we noticed that with each run of the code the pattern would repeat but starting on a different place of the butterfly. We concluded and reported then that it was due to the pseudorandom generator associated with srand() function, but today I found again this report and there are still some things that I would like to understand. I would like to understand better how the pseudorandom generator works in order to obtain this sort of symmetry and ciclic pattern. The pattern I'm talking about is this (The steps are color coded in a rainbow sequence to apreciate the progression of the walk):

EDIT:

I'm adding the code used to obtain this figure:

#include<iostream>
#include<cmath>
#include<stdlib.h>
#include<time.h>
#include <fstream>
#include <string.h>
#include <string>
#include <iomanip>

using namespace std;

int main ()
{
srand(time(NULL));
int num1,n=250000;



ofstream rnd_coordinates("Random2D.txt");
float x=0,y=0,sumx_f=0,sumy_f=0,sum_d=0,d_m,X,t,d;
float x_m,y_m;

x=0;
y=0;

for(int i=0;i<n;i++){

    t=i;
    num1= rand()%4;

    if(num1==0){
        x++;
    }
    if(num1==1){
        x--;
    }
    if(num1==2){
        y++;
    }
    if(num1==3){
        y--;
    }

    rnd_coordinates<<x<<','<<y<<','<<t<<endl;

}

rnd_coordinates.close();


return 0;
}

Edom

We don't know what that picture means. What is meaning of a certain color, or location on the page? How does any of that related to the RNG? – Respirator

Well, I tried to explain it in the text but yes it lacks axis and color legend... It is related to PRNG because it uses a "random number" to go with equal probability either up, down, right or left in succesive steps, starting at the point (0,0). The color is just a reference for the step number, it goes from purple all the way to red in the visible color spectrum. This is the result after 2.5 milion steps. – Edom

Answer 1

You never hit rand()'s period, but keep in mind you don't actually use the entire rand() range that in its entirety guarantees a 2^32 period.

With that in mind, you have 2 options:

1. Use all the bits. rand() returns 2 bytes (16 bits), and you need 2 bits (for 4 possible values). Split that 16 bit output into chunks of 2 bits and use them all in sequence.
2. At the very least if you insist on using the lazy %n way, choose a modulo that's not a divisor of your period. For example choose 5 instead of 4, since 5 is prime, and if you get the 5th value reroll.

Yellowweed

The second option actually solved the problem and I'm obtaining a diferent pattern each time with a lot more steps. If I do even more steps another cyclic pattern would appear? Also, why the symmetry on the butterfly pattern? – Edom

The way rand() is implemented is just a * x + b, and if all you look at is the first 2 bits the period is a lot smaller than the otherwise guaranteed 4 billion. The actual period obviously depends on the a and b values, but you can math it out from your own C++ RT implementation if you want. I think overall it's just blind luck that you hit an easily recognizable pattern that fast. – Yellowweed

And keep in mind that the modulo operation skews your random distribution towards 0. A better operation is to divide by the maximum value in the floating point space. And both issues would be averted in this case by the simple fact that your 2 required bits can easily be extracted from the 16 bit result (16 % 2 = 0), just use all the bits and you get the full use of your period! – Yellowweed

Answer 2

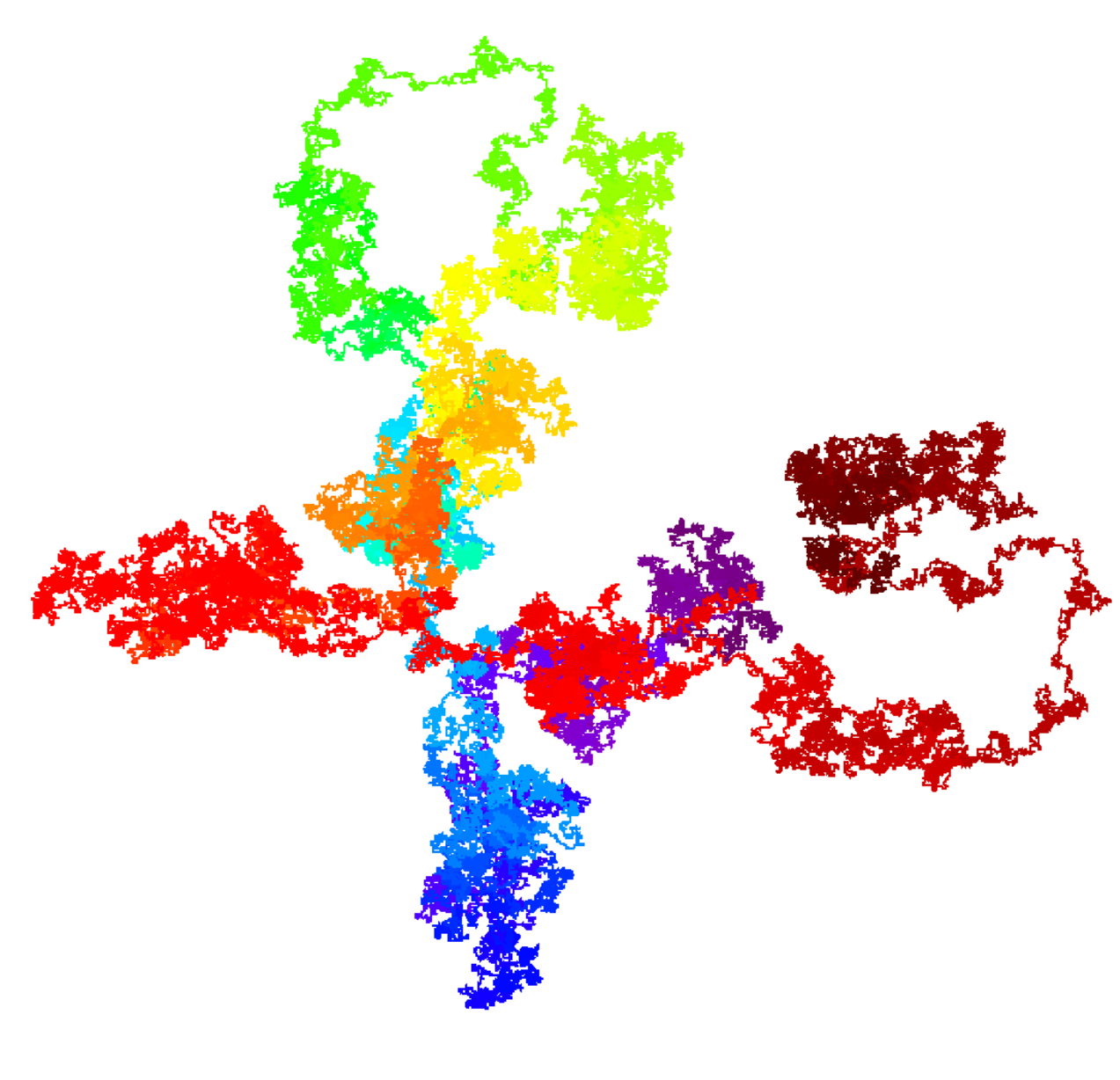
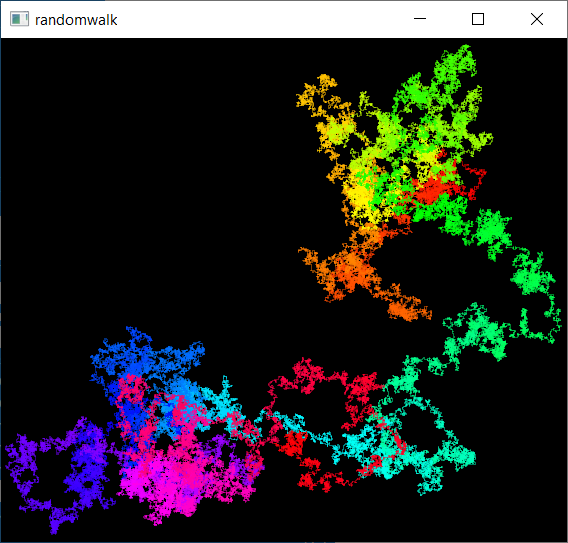
The code below constitutes a complete compileable example.

Your issue is with dropping bits from the random generator. Lets's see how one could write a source of random bit pairs that doesn't drop bits. It requires that RAND_MAX is of the form 2^n−1, but the idea could be extended to support any RAND_MAX >= 3.

#include <cassert>
#include <cstdint>
#include <cstdlib>

class RandomBitSource {
    int64_t bits = rand();
    int64_t bitMask = RAND_MAX;
    static_assert((int64_t(RAND_MAX + 1) & RAND_MAX) == 0, "No support for RAND_MAX != 2^(n-1)");
public:
    auto get2Bits() {
        if (!bitMask) // got 0 bits
            bits = rand(), bitMask = RAND_MAX;
        else if (bitMask == 1) // got 1 bit
            bits = (bits * (RAND_MAX+1)) | rand(), bitMask = (RAND_MAX+1) | RAND_MAX;

        assert(bitMask & 3);
        bitMask >>= 2;
        int result = bits & 3;
        bits >>= 2;
        return result;
    }
};

Then, the random walk implementation could be as follows. Note that the ' digit separator is a C++14 feature - quite handy.

#include <vector>

using num_t = int;
struct Coord { num_t x, y; };

struct Walk {
    std::vector<Coord> points;
    num_t min_x = {}, max_x = {}, min_y = {}, max_y = {};
    Walk(size_t n) : points(n) {}
};

auto makeWalk(size_t n = 250'000)
{
    Walk walk { n };
    RandomBitSource src;
    num_t x = 0, y = 0;

    for (auto& point : walk.points)
    {
        const int bits = src.get2Bits(), b0 = bits & 1, b1 = bits >> 1;
        x = x + (((~b0 & ~b1) & 1) - ((b0 & ~b1) & 1));
        y = y + (((~b0 & b1) & 1) - ((b0 & b1) & 1));

        if (x < walk.min_x)
            walk.min_x = x;
        else if (x > walk.max_x)
            walk.max_x = x;
        if (y < walk.min_y)
            walk.min_y = y;
        else if (y > walk.max_y)
            walk.max_y = y;

        point = { x, y };
    }
    return walk;
}

With a bit more effort, we can make this into an interactive Qt application. Pressing Return generates a new image.

The image is viewed at the native resolution of the screen it's displayed on, i.e. it maps to physical device pixels. The image is not scaled. Instead, it is rotated when needed to better fit into the screen's orientation (portrait vs landscape). That's for portrait monitor aficionados :)

#include <QtWidgets>

QImage renderWalk(const Walk& walk, Qt::ScreenOrientation orient)
{
    using std::swap;
    auto width = walk.max_x - walk.min_x + 3;
    auto height = walk.max_y - walk.min_y + 3;
    bool const rotated = (width < height) == (orient == Qt::LandscapeOrientation);
    if (rotated) swap(width, height);
    QImage image(width, height, QPixmap(1, 1).toImage().format());
    image.fill(Qt::black);

    QPainter p(&image);
    if (rotated) {
        p.translate(width, 0);
        p.rotate(90);
    }
    p.translate(-walk.min_x, -walk.min_y);

    auto constexpr hueStep = 1.0/720.0;
    qreal hue = 0;
    int const huePeriod = walk.points.size() * hueStep;
    int i = 0;
    for (auto& point : walk.points) {
        if (!i--) {
            p.setPen(QColor::fromHsvF(hue, 1.0, 1.0, 0.5));
            hue += hueStep;
            i = huePeriod;
        }
        p.drawPoint(point.x, point.y);
    }
    return image;
}

#include <ctime>

int main(int argc, char* argv[])
{
    srand(time(NULL));
    QApplication a(argc, argv);
    QLabel view;
    view.setAlignment(Qt::AlignCenter);
    view.setStyleSheet("QLabel {background-color: black;}");
    view.show();

    auto const refresh = [&view] {
        auto *screen = view.screen();
        auto orientation = screen->orientation();
        auto pixmap = QPixmap::fromImage(renderWalk(makeWalk(), orientation));
        pixmap.setDevicePixelRatio(screen->devicePixelRatio());
        view.setPixmap(pixmap);
        view.resize(view.size().expandedTo(pixmap.size()));
    };
    refresh();
    QShortcut enter(Qt::Key_Return, &view);
    enter.setContext(Qt::ApplicationShortcut);
    QObject::connect(&enter, &QShortcut::activated, &view, refresh);
    return a.exec();
}

Electrosurgery

Answer 3

Every pseudorandom generator is a cycle of some sequence of numbers. One of the ways we distinguish "good" prngs from "bad" prngs is the length of this sequence. There is some state associated with the generator, so the maximum period is bounded by how many distinct states there are.

Your implementation has a "short" period, because it repeats in less than the age of the universe. It probably has 32 bits of state, so the period is at most 2^32.

As you are using C++, you can try again using a randomly seeded std::mt19937, and you won't see repeats.

Barbate

"and you won't see repeats" even if true, that is a terrible deduction. You mentioned a period of 2^32 and he didn't generate 4 billion numbers, so he never hit the period. – Yellowweed

Yes I didn't hit that period. I understand what the answer says about prngs but what I want to understand is why the pattern in the random walk case repeats itself with the symmetry displayed and then closes on itself... Is the sequence mirrored in some way? – Edom

The sequence can be mirrored, of course. It can do anything in fact. It just so happens that for the particular number of points you chose (250'000), there's a mirror image in the lower bits of the sequence you're using. Choose a different RNG and you won't see the same effect. It's an artifact of incorrect use of rand()'s output, and the choice of the RNG. – Shebashebang

Answer 4

You might want to look at my answer to another question here about older rand() implementations. Sometimes with the old rand() and srand() functions the lower order bits are much less random than the higher order bits. Some of these older implementations still persist, it's possible you used one.

Truelove