How to fix this non-recursive odd-even-merge sort algorithm?

Question

I was searching for non-recursive odd-even-merge sort algorithm and found 2 sources:

• a book from Sedgewick R.
• this SO question

Both algorithms are identical but false. The resulting sorting network is not an odd-even-merge sort network.

Here is an image of the resulting network with 32 inputs. A vertical line between 2 horizontal lines means compare value a[x] with a[y], if greater then swap the values in the array.

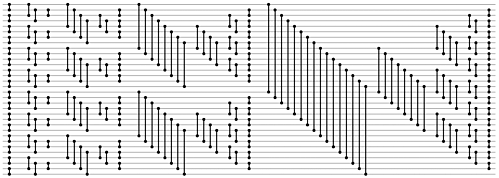
_{(source: flylib.com)}
(clickable)

I copied the code from Java to C and replaced the exch function by a printf to print the exchange candidates.

When one draws a diagram of the pairs, it can be seen that too many pairs are generated.

Has anyone an idea how to fix this algorithm?

Why do I need non-recursive version?
I want to transform this sorting network into hardware. It's easy to insert pipeline stages into a non-recursive algorithms.

I also investigated the recursive version, but it's too complex to transform the algorithm into pipelined hardware.

My C code:

#include <stdlib.h>
#include <stdio.h>

void sort(int l, int r)
{ int n = r-l+1;

  for (int p=1; p<n; p+=p)
    for (int k=p; k>0; k/=2)
      for (int j=k%p; j+k<n; j+=(k+k))
        for (int i=0; i<n-j-k; i++)
          if ((j+i)/(p+p) == (j+i+k)/(p+p))
              printf("%2i cmp %2i\n", l+j+i, l+j+i+k);
}
int main(char* argv, int args)
{ const int COUNT = 8;
  sort(0, COUNT);
}

The result:

0 -o--------o-------------------------o---------------o-------------------------
   |        |                         |               |
1 -o--------|-o------o----------------|-o-------------o-o-----------------------
            | |      |                | |               |
2 -o-o------o-|------o-o--------------|-|-o----o--------o-o---------------------
   | |        |        |              | | |    |          |
3 -o-o--------o--------o--------------|-|-|-o--|-o--------o-o-------o-----------
                                      | | | |  | |          |       |
4 -o-o-o----o---o----o-----o----------o-|-|-|--o-|-o--------o-o-----o-o---------
   | | |    |   |    |     |            | | |    | |          |       |
5 -o-o-o----|-o-|-o--o-o---o-o---o------o-|-|----o-|-o--------o-o-----o-o---o---
            | | | |    |     |   |        | |      | |          |       |   |
6 -o-o-o-o--o-|-o-|----o-o---o-o-o-o------o-|------o-|----------o-o-----o-o-o-o-
   | | | |    |   |      |     |   |        |        |            |       |   |
7 -o-o-o-o----o---o------o-----o---o--------o--------o------------o-------o---o-

When I know the correct exchange pairs and the algorithm is equal to the image, I'll translate it into VHDL for tests on my hardware platform.

Other open source hardware sorting network implementations:

• PoC.sort.sortnet.oddevensort
• PoC.sort.sortnet.bitonicsort

---

Appendix:
Odd-even mergesort (a.k.a Batcher's sort) is like bitonic sort (not to confuse with Batcher's bitonic sort). But in hardware this algorithm has a better size complexity than bitonic sort, while latency is the same.

These algorithm can be implemented with good resource usage compared to fast software algorithms like quicksort.

Wikipedia: odd-even mergesort

Note:
Because sorting networks are static and independent of the input values, no compare and swap is needed to generate the network. That's one reason why it can be transformed into hardware. My code generates the indices for the compare operations. In hardware, these vertical connections will be replaced by compare and swap circuits. So unsorted data will travel throught the network and on the output side it will be sorted.

Kimberliekimberlin

Not sure how hard you are going to be on efficiency, but if the final result is accurate, does it really matter if it generates too many pairs during the process? – Rockweed

YES. In software it generates masses of compare operation with a big cache pollution. In hardware it increases area consumption and latency. Normally odd-even-merge sort has a O(N * log N * log N) size complexity. My diagram looks like N^3. – Kimberliekimberlin

I don't understand: what do you dislike about the current algorithm? Why do you claim it generates too many pairs? Is there a particular pair that you are sure is unnecessary? What is an odd-even merge sort? – Donte

Right! I understand what you mean, the concept, etc... however I am not deeply knowledged enough in Math algorithms to help you much. Hopefully someone can help you. – Rockweed

Maybe this helps? academia.edu/9035484/…. Try dsp.stackexchange.com – Fife

I finished my result diagram as ASCII-art :). – Kimberliekimberlin

Thanks, Paebbels. It is much clearer what the problem is now. The 2-3, 4-5, and 6-7 sorts in the second column are clearly redundant. – Donte

I think I found a solution. Can anybody check my code or should I ask this on CR.SE? – Kimberliekimberlin

Answer 1

I think I found a solution. I checked it for length = 2, 4, 8, 16.

Here is my code:

void sort(int length)
{ int G = log2ceil(length);                      // number of groups
  for (int g = 0; g < G; g++)                    // iterate groups
  { int B = 1 << (G - g - 1);                    // number of blocks
    for (int b = 0; b < B; b++)                  // iterate blocks in a group
    { for (int s = 0; s <= g; s++)               // iterate stages in a block
      { int d = 1 << (g - s);                    // compare distance
        int J = (s == 0) ? 0 : d;                // starting point
        for (int j = J; j+d < (2<<g); j += 2*d)  // iterate startpoints
        { for (int i = 0; i < d; i++)            // shift startpoints
          { int x = (b * (length / B)) + j + i;  // index 1
            int y = x + d;                       // index 2
            printf("%2i cmp %2i\n", x, y);
          }
        }
      }
   }
}

This solution introduces a fifth for-loop to handle subblocks in a group. The j loop has a changed start and abort value to handle odd counts of post merge steps without generating doubled compare steps.

Kimberliekimberlin

Answer 2

The following code works for arrays of any size and isn't recursive. It is a straight port from the implementation of the corresponding function in Perl's Algorithm::Networksort module. The implementation happens to correspond to the algorithm as described by Knuth in The Art of Computer Programming, vol 3 (algorithm 5.2.2M). It doesn't help to actually fix your algorithm, but it at least gives you a working non-recursive implementation of Batcher's odd-even mergesort with only three nested loops :)

#include <math.h>
#include <stdio.h>

void oddeven_merge_sort(int length)
{
    int t = ceil(log2(length));
    int p = pow(2, t - 1);

    while (p > 0) {
        int q = pow(2, t - 1);
        int r = 0;
        int d = p;

        while (d > 0) {
            for (int i = 0 ; i < length - d ; ++i) {
                if ((i & p) == r) {
                    printf("%2i cmp %2i\n", i, i + d);
                }
            }

            d = q - p;
            q /= 2;
            r = p;
        }
        p /= 2;
    }
}

If you can get your hands on a copy of The Art of Computer Programming, vol 3, you will have a nice explanation of how and why the algorithm works, as well as a few additional details.

Social

I'll try to find this book in the library. – Kimberliekimberlin

Answer 3

This is a fixed non-recursive subroutine.

void sort(int n)
{
  for (int p = 1; p < n; p += p)
    for (int k = p; k > 0; k /= 2)
      for (int j = k % p; j + k < n; j += k + k)
        //for (int i = 0; i < n - (j + k); i++) // wrong
        for (int i = 0; i < k; i++) // correct
          if ((i + j)/(p + p) == (i + j + k)/(p + p))
            printf("%2i cmp %2i\n", i + j, i + j + k);
}

or

void sort(int n)
{
  for (int p = 1; p < n; p += p)
    for (int k = p; k > 0; k /= 2)
      for (int j = 0; j < k; j++)
        for (int i = k % p; i + k < n; i += k + k)
          if ((i + j)/(p + p) == (i + j + k)/(p + p))
            printf("%2i cmp %2i\n", i + j, i + j + k);
}

Dyandyana