Imo, the missing piece of key information with most explanations of consistent hashing is that they don't detail the part about "multiple hash functions."
For whatever reason, most "consistent hashing for dummies" articles gloss over the implementation detail that makes the virtual nodes work with random distribution.
Before talking about how it does work, let me clarify the above with an example of how it does not work.
How it does not work
A naive implementation of vnodes looks like this:
![naive vnodes]() source
source
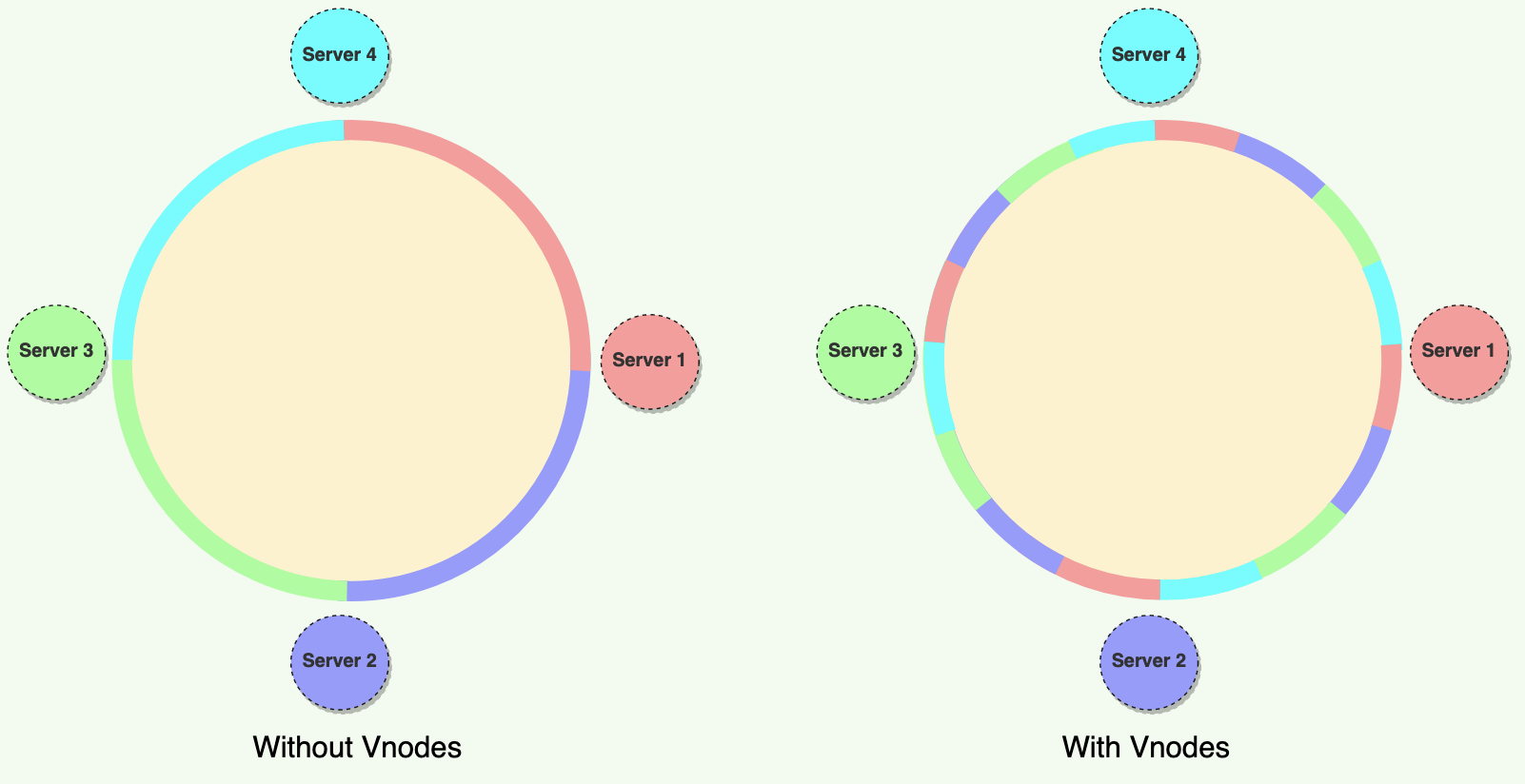
This is naive because you'll notice that, for example, the green vnode always precedes the blue vnode. This means that if the green vnode goes offline then it will be replaced solely by the blue vnode, which defeats the entire purpose of moving from single-token nodes to distributed virtual nodes.
The article quickly mentions that practically, Vnodes are randomly distributed across the cluster. It then shows a separate picture indicating this but without explaining the mechanics of how this is achieved.
How it does work
Random distribution of vnodes is achieved via the use of multiple, unique hash functions. These multiple functions are where the random distribution comes from.
This makes the implementation look something roughly like this:
A) Ring Formation
- You have a ring consisting of
n physical nodes via physical_nodes = ['192.168.1.1', '192.168.1.2', '192.168.1.3', '192.168.1.4']; (think of this as B/R/P/G in the prior picture's left-side)
- You decide to distribute each physical node into
k "virtual slices," i.e. a single physical node is sliced into k pieces
- In this example, we use
k = 4, but in practice we use should use k ≈ log2(num_items) to obtain reasonably balanced loads for storing a total of num_items in the entire datastore
- This means that
num_virtual_nodes == n * k; (this corresponds to the 16 pieces in the prior picture's right-side)
- Assign a unique hashing algo for each
k via hash_funcs = [md5, sha, crc, etc]
- (You can also use a single function that is recursively called
k times)
- Divy up the ring by the following:
virtual_physical_map = {}
virtual_node_ids = []
for hash_func in hash_funcs:
for physical_node in physical_nodes:
virtual_hash = hash_func(physical_node)
virtual_node_ids.append(virtual_hash)
virtual_physical_map[virtual_hash] = physical_node
virtual_node_ids.sort()
You now have a ring composed of n * k virtual nodes, which are randomly distributed across the n physical nodes.
B) Partition Request Flow
- A partition-request is made with a provided
key_tuple to key off of
- The
key_tuple is hashed to get key_hash
- Find the next clock-wise node via
virtual_node = binary_search(key_hash, virtual_node_ids)
- Lookup the real node via
physical_id = virtual_physical_map[virtual_node]
Page 6 of this Stanford Lecture was very helpful to me in understanding this.
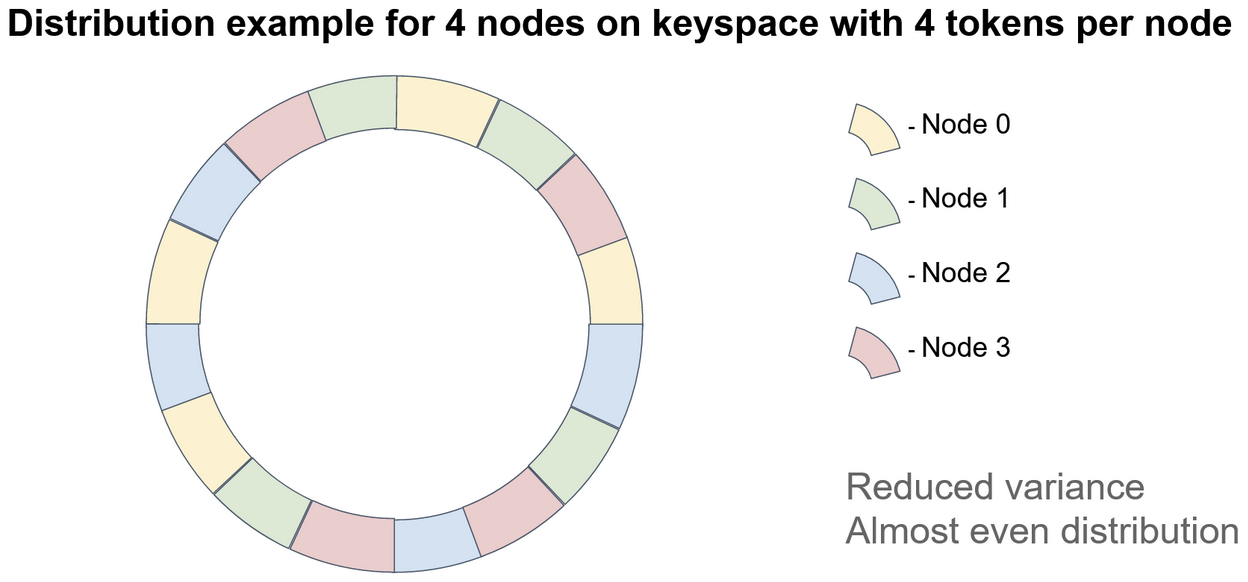
The net effect is that the distribution of vnodes across the ring looks like this:
![distributed vnodes]() source
source