I wrote a function that multiplies Eigen matrices of dimension 10x10 together. Then I wrote a naive multiply function CustomMultiply which was surprisingly 2x faster than Eigen's implementation.
I tried a couple of different compilation flags like -O2 and -O3, which did not make a difference.
#include <Eigen/Core>
constexpr int dimension = 10;
using Matrix = Eigen::Matrix<double, dimension, dimension>;
Matrix CustomMultiply(const Matrix& a, const Matrix& b) {
Matrix result = Matrix::Zero();
for (int bcol_idx = 0; bcol_idx < dimension; ++bcol_idx) {
for (int brow_idx = 0; brow_idx < dimension; ++brow_idx) {
result.col(bcol_idx).noalias() += a.col(brow_idx) * b(brow_idx, bcol_idx);
}
}
return result;
}
Matrix PairwiseMultiplyEachMatrixNoAlias(int num_repetitions, const std::vector<Matrix>& input) {
Matrix acc = Matrix::Zero();
for (int i = 0; i < num_repetitions; ++i) {
for (const auto& matrix_a : input) {
for (const auto& matrix_b : input) {
acc.noalias() += matrix_a * matrix_b;
}
}
}
return acc;
}
Matrix PairwiseMultiplyEachMatrixCustom(int num_repetitions, const std::vector<Matrix>& input) {
Matrix acc = Matrix::Zero();
for (int i = 0; i < num_repetitions; ++i) {
for (const auto& matrix_a : input) {
for (const auto& matrix_b : input) {
acc.noalias() += CustomMultiply(matrix_a, matrix_b);
}
}
}
return acc;
}
PairwiseMultiplyEachMatrixNoAlias is 2x slower on PairwiseMultiplyEachMatrixCustom on my machine when I pass in 100 random matrices as input and use 100 as num_repetitions.
My machine details: Intel Xeon CPU E5-2630 v4, Ubuntu 16.04, Eigen 3
Updates: Results are unchanged after the following modifications after helpful discussion in the comments
num_repetitions = 1andinput.size() = 1000- using
.lazyProduct()and using.eval()actually leads to further slowdown - clang 8.0.0
- g++ 9.2
- using flags
-march=native -DNDEBUG
Updates 2:
Following up on @dtell's findings with Google Benchmark library, I found an interesting result. Multiplying 2 matrices with Eigen is faster than custom, but multiplying many matrices with Eigen is 2x slower, in line with the previous findings.
Here is my Google Benchmark code. (Note: There was an off-by one in the GenerateRandomMatrices() function below which is now fixed.)
#include <Eigen/Core>
#include <Eigen/StdVector>
#include <benchmark/benchmark.h>
constexpr int dimension = 10;
constexpr int num_random_matrices = 10;
using Matrix = Eigen::Matrix<double, dimension, dimension>;
using Eigen_std_vector = std::vector<Matrix,Eigen::aligned_allocator<Matrix>>;
Eigen_std_vector GetRandomMatrices(int num_matrices) {
Eigen_std_vector matrices;
for (int i = 0; i < num_matrices; ++i) {
matrices.push_back(Matrix::Random());
}
return matrices;
}
Matrix CustomMultiply(const Matrix& a, const Matrix& b) {
Matrix result = Matrix::Zero();
for (int bcol_idx = 0; bcol_idx < dimension; ++bcol_idx) {
for (int brow_idx = 0; brow_idx < dimension; ++brow_idx) {
result.col(bcol_idx).noalias() += a.col(brow_idx) * b(brow_idx, bcol_idx);
}
}
return result;
}
Matrix PairwiseMultiplyEachMatrixNoAlias(int num_repetitions, const Eigen_std_vector& input) {
Matrix acc = Matrix::Zero();
for (int i = 0; i < num_repetitions; ++i) {
for (const auto& matrix_a : input) {
for (const auto& matrix_b : input) {
acc.noalias() += matrix_a * matrix_b;
}
}
}
return acc;
}
Matrix PairwiseMultiplyEachMatrixCustom(int num_repetitions, const Eigen_std_vector& input) {
Matrix acc = Matrix::Zero();
for (int i = 0; i < num_repetitions; ++i) {
for (const auto& matrix_a : input) {
for (const auto& matrix_b : input) {
acc.noalias() += CustomMultiply(matrix_a, matrix_b);
}
}
}
return acc;
}
void BM_PairwiseMultiplyEachMatrixNoAlias(benchmark::State& state) {
// Perform setup here
const auto random_matrices = GetRandomMatrices(num_random_matrices);
for (auto _ : state) {
benchmark::DoNotOptimize(PairwiseMultiplyEachMatrixNoAlias(1, random_matrices));
}
}
BENCHMARK(BM_PairwiseMultiplyEachMatrixNoAlias);
void BM_PairwiseMultiplyEachMatrixCustom(benchmark::State& state) {
// Perform setup here
const auto random_matrices = GetRandomMatrices(num_random_matrices);
for (auto _ : state) {
benchmark::DoNotOptimize(PairwiseMultiplyEachMatrixCustom(1, random_matrices));
}
}
BENCHMARK(BM_PairwiseMultiplyEachMatrixCustom);
void BM_MultiplySingle(benchmark::State& state) {
// Perform setup here
const auto random_matrices = GetRandomMatrices(2);
for (auto _ : state) {
benchmark::DoNotOptimize((random_matrices[0] * random_matrices[1]).eval());
}
}
BENCHMARK(BM_MultiplySingle);
void BM_MultiplySingleCustom(benchmark::State& state) {
// Perform setup here
const auto random_matrices = GetRandomMatrices(2);
for (auto _ : state) {
benchmark::DoNotOptimize(CustomMultiply(random_matrices[0], random_matrices[1]));
}
}
BENCHMARK(BM_MultiplySingleCustom);
double TestCustom() {
const Matrix a = Matrix::Random();
const Matrix b = Matrix::Random();
const Matrix c = a * b;
const Matrix custom_c = CustomMultiply(a, b);
const double err = (c - custom_c).squaredNorm();
return err;
}
// Just sanity check the multiplication
void BM_TestCustom(benchmark::State& state) {
if (TestCustom() > 1e-10) {
exit(-1);
}
}
BENCHMARK(BM_TestCustom);
This yields the following mysterious report
Run on (20 X 3100 MHz CPU s)
CPU Caches:
L1 Data 32K (x10)
L1 Instruction 32K (x10)
L2 Unified 256K (x10)
L3 Unified 25600K (x1)
***WARNING*** CPU scaling is enabled, the benchmark real time measurements may be noisy and will incur extra overhead.
----------------------------------------------------------------------------
Benchmark Time CPU Iterations
----------------------------------------------------------------------------
BM_PairwiseMultiplyEachMatrixNoAlias 28283 ns 28285 ns 20250
BM_PairwiseMultiplyEachMatrixCustom 14442 ns 14443 ns 48488
BM_MultiplySingle 791 ns 791 ns 876969
BM_MultiplySingleCustom 874 ns 874 ns 802052
BM_TestCustom 0 ns 0 ns 0
My current hypothesis is that the slowdown is attributable to instruction cache misses. It's possible Eigen's matrix multiply function does bad things to the instruction cache.
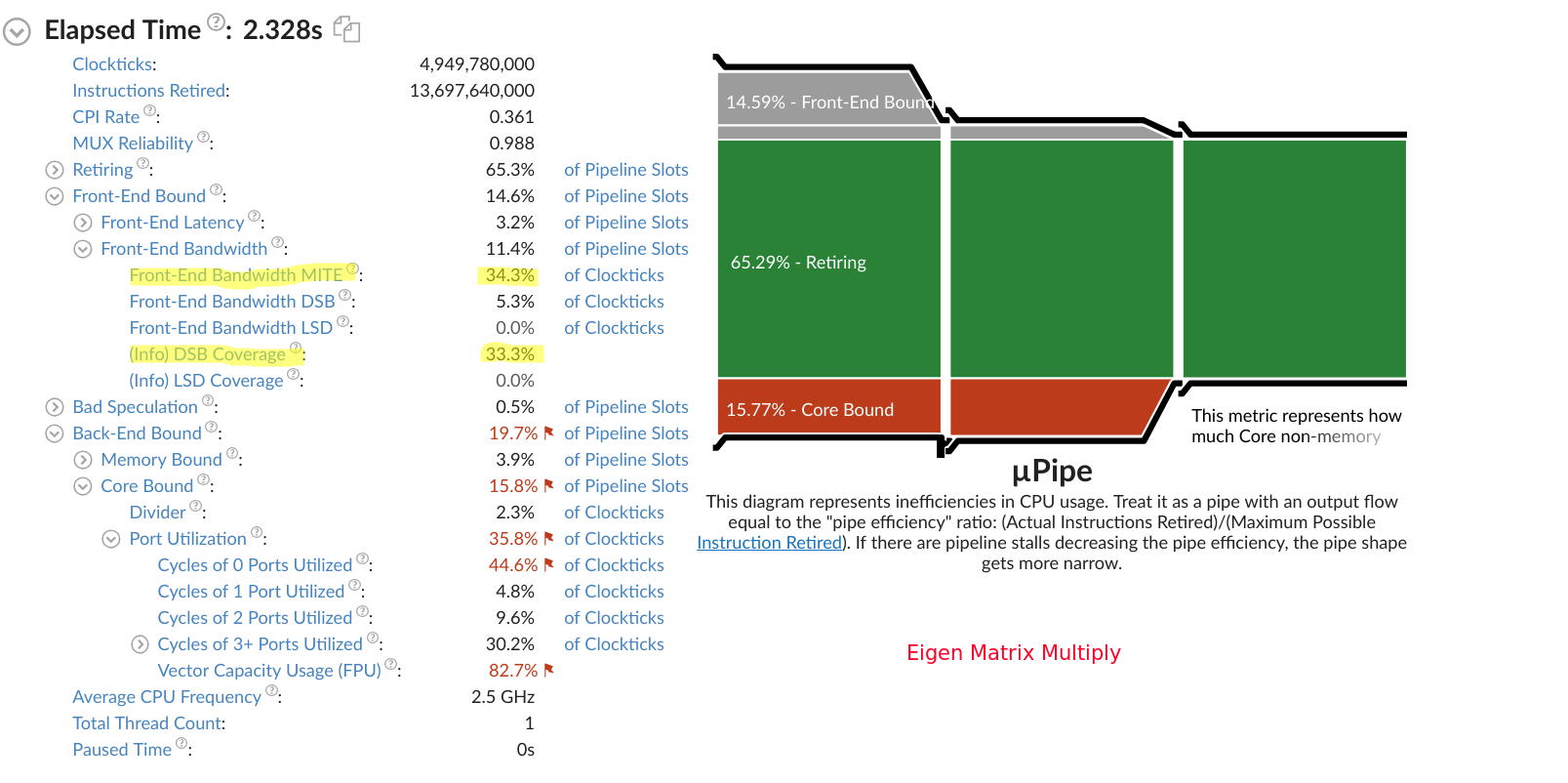
Maybe someone with more experience with VTune can tell me if I am interpreting this result correctly. The DSB is the decoded instruction cache and MITE has something to do with instruction decoder bandwidth. The Eigen version shows that most instructions are missing the DSB (66% miss rate) and a marked increase in stalling due to MITE bandwidth.
Update 3: After getting reports that the single version of custom was faster, I also reproduced it on my machine. This goes against @dtell's original findings on their machine.
CPU Caches:
L1 Data 32K (x10)
L1 Instruction 32K (x10)
L2 Unified 256K (x10)
L3 Unified 25600K (x1)
***WARNING*** CPU scaling is enabled, the benchmark real time measurements may be noisy and will incur extra overhead.
----------------------------------------------------------------------------
Benchmark Time CPU Iterations
----------------------------------------------------------------------------
BM_PairwiseMultiplyEachMatrixNoAlias 34787 ns 34789 ns 16477
BM_PairwiseMultiplyEachMatrixCustom 17901 ns 17902 ns 37759
BM_MultiplySingle 349 ns 349 ns 2054295
BM_MultiplySingleCustom 178 ns 178 ns 4624183
BM_TestCustom 0 ns 0 ns 0
I wonder if in my previous benchmark result I had left out an optimization flag. In any case, I think the issue is confirmed that Eigen incurs an overhead when multiplying small matrices. If anyone out there has a machine that does not use a uop cache, I would be interested in seeing if the slowdown is less severe.


-O2. – Disc-march=native -O2 -DNDEBUGand can you trymatrix_a.lazyProduct(matrix_b)instead ofmatrix_a * matrix_b? It appears to me that the threshold for switching to the cache-optimized GEMM is set too low. – Billingsleyconst. For that reason, I have repeated the benchmark forinput = 1andnum_matrices = 1000and found the same effect – Nightly.noalias()+=on col/rows avoids allocation in both cases. In theory thematrix += a*bcould be done with no actual allocation of a matrix, whilematrix += custommult(a,b)cannot as written. – WhopperlazyProductsped up the computation, but not as much as the naive version - only 1.5x slower than naive. – Nightly.noalias()might block evaluate-before-assigning flag on the right (unless the cost model says do it anyhow)? Then if the cost model is off on your hardware, it might spend more time than needed? Try a(matrix_a * matrix_b).eval(); that should make the*code run for certain, which is what your naive version does. – Whopper.eval()did not help, and neither did the raw expressionacc += matrix_a * matrix_b;.noalias()leads to a consistent speedup on my machine. – Nightly