Is it possible to add a UILabel or CATextLayer to a CGPath in Swift, similar to Photoshop's type to path feature?

You'll need to do this by hand, by computing the Bezier function and its slope at each point you care about, and then drawing a glyph at that point and rotation. You'll need to know 4 points (traditionally called P0-P3). P0 is the starting point of the curve. P1 and P2 are the control points. And P3 is the ending point in the curve.

The Bezier function is defined such that as the "t" parameter moves from 0 to 1, the output will trace the desired curve. It's important to know here that "t" is not linear. t=0.25 does not necessarily mean "1/4 of the way along the curve." (In fact, that's almost never true.) This means that measuring distances long the curve is a little tricky. But we'll cover that.

First, you'll need the core functions and a helpful extension on CGPoint:

// The Bezier function at t
func bezier(_ t: CGFloat, _ P0: CGFloat, _ P1: CGFloat, _ P2: CGFloat, _ P3: CGFloat) -> CGFloat {
           (1-t)*(1-t)*(1-t)         * P0
     + 3 *       (1-t)*(1-t) *     t * P1
     + 3 *             (1-t) *   t*t * P2
     +                         t*t*t * P3
}

// The slope of the Bezier function at t
func bezierPrime(_ t: CGFloat, _ P0: CGFloat, _ P1: CGFloat, _ P2: CGFloat, _ P3: CGFloat) -> CGFloat {
       0
    -  3 * (1-t)*(1-t) * P0
    + (3 * (1-t)*(1-t) * P1) - (6 * t * (1-t) * P1)
    - (3 *         t*t * P2) + (6 * t * (1-t) * P2)
    +  3 * t*t * P3
}

extension CGPoint {
    func distance(to other: CGPoint) -> CGFloat {
        let dx = x - other.x
        let dy = y - other.y
        return hypot(dx, dy)
    }
}

t*t*t is dramatically faster than using the pow function, which is why the code is written this way. These functions will be called a lot, so they need to be reasonably fast.

Then there is the view itself:

class PathTextView: UIView { ... }

First it includes the control points, and the text:

var P0 = CGPoint.zero
var P1 = CGPoint.zero
var P2 = CGPoint.zero
var P3 = CGPoint.zero

var text: NSAttributedString {
    get { textStorage }
    set {
        textStorage.setAttributedString(newValue)
        locations = (0..<layoutManager.numberOfGlyphs).map { [layoutManager] glyphIndex in
            layoutManager.location(forGlyphAt: glyphIndex)
        }

        lineFragmentOrigin = layoutManager
            .lineFragmentRect(forGlyphAt: 0, effectiveRange: nil)
            .origin
    }
}

Every time the text is changed, the layoutManager recomputes the locations of all of the glyphs. We'll later adjust those values to fit the curve, but these are the baseline. The positions are the positions of each glyph relative to the fragment origin, which is why we need to keep track of that, too.

Some odds and ends:

private let layoutManager = NSLayoutManager()
private let textStorage = NSTextStorage()

private var locations: [CGPoint] = []
private var lineFragmentOrigin = CGPoint.zero

init() {
    textStorage.addLayoutManager(layoutManager)
    super.init(frame: .zero)
    backgroundColor = .clear
}

required init?(coder: NSCoder) { fatalError("init(coder:) has not been implemented") }

The Bezier function is actually a one-dimensional function. In order to use it in two dimensions, we call it twice, once for x and once for y, and similarly to compute the rotations at each point.

func getPoint(forOffset t: CGFloat) -> CGPoint {
    CGPoint(x: bezier(t, P0.x, P1.x, P2.x, P3.x),
            y: bezier(t, P0.y, P1.y, P2.y, P3.y))
}

func getAngle(forOffset t: CGFloat) -> CGFloat {
    let dx = bezierPrime(t, P0.x, P1.x, P2.x, P3.x)
    let dy = bezierPrime(t, P0.y, P1.y, P2.y, P3.y)
    return atan2(dy, dx)
}

One last piece of housekeeping, and it'll be time to dive into the real function. We need a way to compute how much we must change "t" (the offset) in order to move a certain distance along the path. I do not believe there is any simple way to compute this, so instead we iterate to approximate it.

// Simplistic routine to find the offset along Bezier that is
// aDistance away from aPoint. anOffset is the offset used to
// generate aPoint, and saves us the trouble of recalculating it
// This routine just walks forward until it finds a point at least
// aDistance away. Good optimizations here would reduce the number
// of guesses, but this is tricky since if we go too far out, the
// curve might loop back on leading to incorrect results. Tuning
// kStep is good start.
func getOffset(atDistance distance: CGFloat, from point: CGPoint, offset: CGFloat) -> CGFloat {
    let kStep: CGFloat = 0.001 // 0.0001 - 0.001 work well
    var newDistance: CGFloat = 0
    var newOffset = offset + kStep
    while newDistance <= distance && newOffset < 1.0 {
        newOffset += kStep
        newDistance = point.distance(to: getPoint(forOffset: newOffset))
    }
    return newOffset
}

OK, finally! Time to draw something.

override func draw(_ rect: CGRect) {

    let context = UIGraphicsGetCurrentContext()!

    var offset: CGFloat = 0.0
    var lastGlyphPoint = P0
    var lastX: CGFloat = 0.0

    // Compute location for each glyph, transform the context, and then draw
    for (index, location) in locations.enumerated() {
        context.saveGState()

        let distance = location.x - lastX
        offset = getOffset(atDistance: distance, from: lastGlyphPoint, offset: offset)

        let glyphPoint = getPoint(forOffset: offset)
        let angle = getAngle(forOffset: offset)

        lastGlyphPoint = glyphPoint
        lastX = location.x

        context.translateBy(x: glyphPoint.x, y: glyphPoint.y)
        context.rotate(by: angle)

        // The "at:" in drawGlyphs is the origin of the line fragment. We've already adjusted the
        // context, so take that back out.
        let adjustedOrigin = CGPoint(x: -(lineFragmentOrigin.x + location.x),
                                     y: -(lineFragmentOrigin.y + location.y))

        layoutManager.drawGlyphs(forGlyphRange: NSRange(location: index, length: 1),
                                 at: adjustedOrigin)

        context.restoreGState()
    }
}

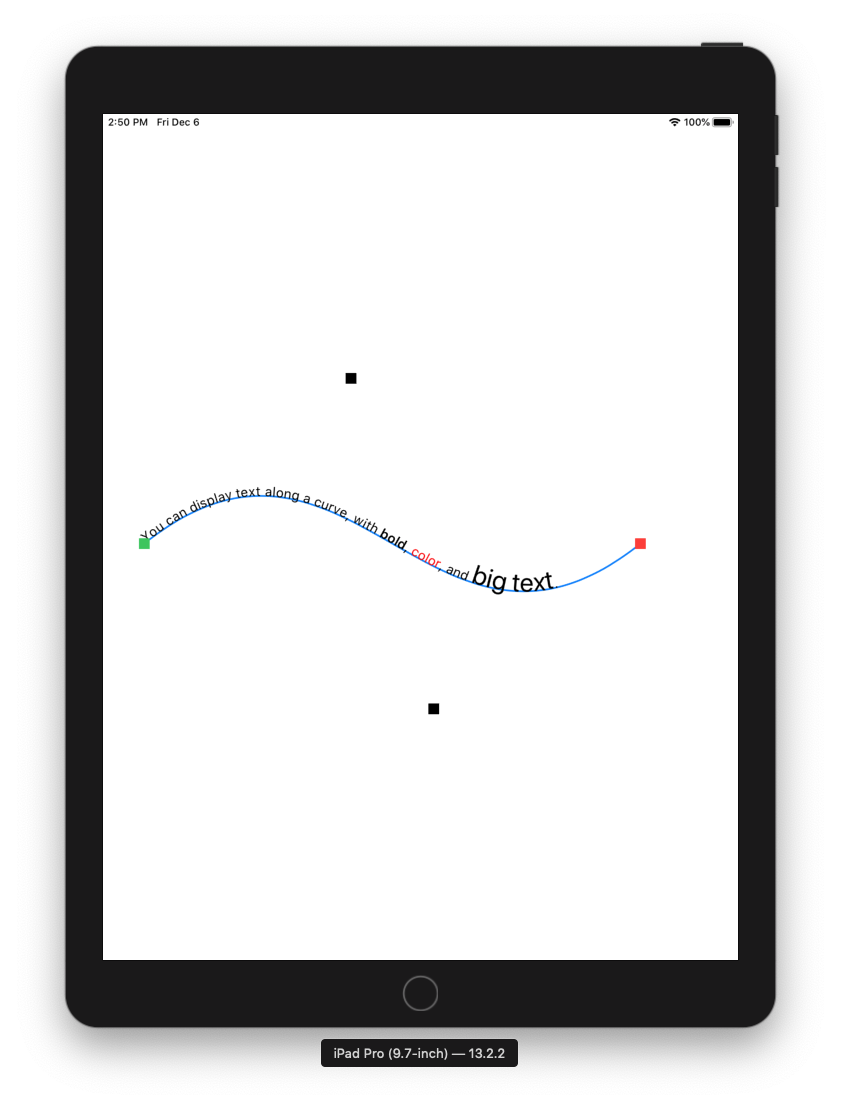
And with that you can draw text along any cubic Bezier.

This doesn't handle arbitrary CGPaths. It's explicitly for cubic Bezier. It's pretty straightforward to adjust this to work along any of the other types of paths (quad curves, arcs, lines, and even rounded rects). However, dealing with multi-element paths opens up a lot more complexity.

For a complete example using SwiftUI, see CurvyText.

Recommended topics

Hot tags