Why does SymPy calculate wrong intersections of planes?

Question

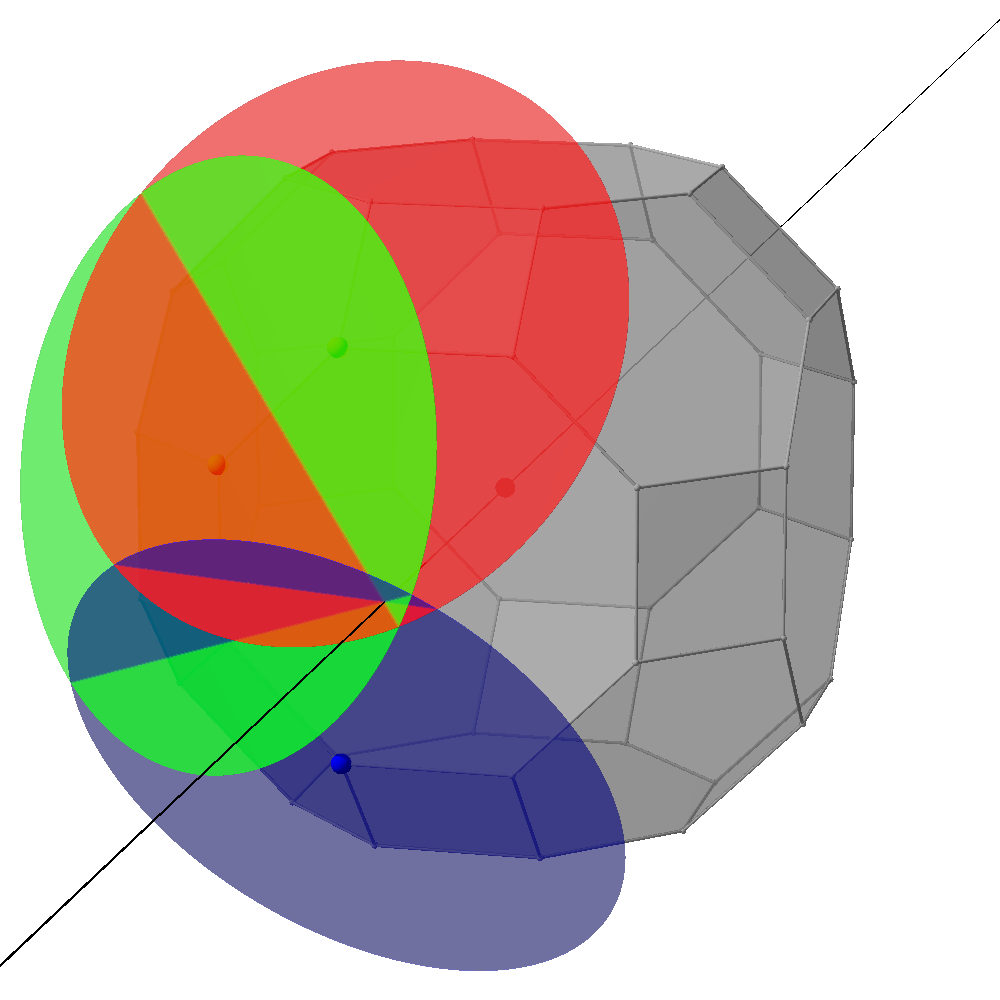
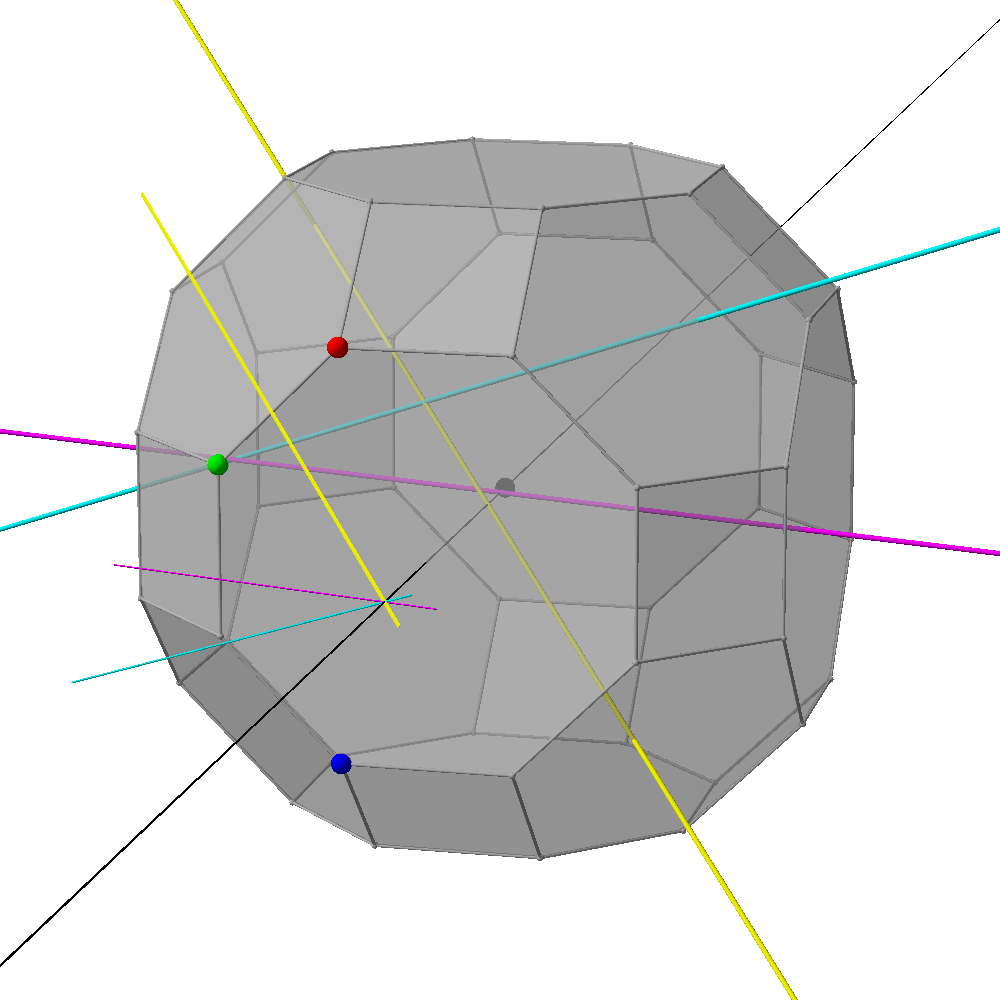
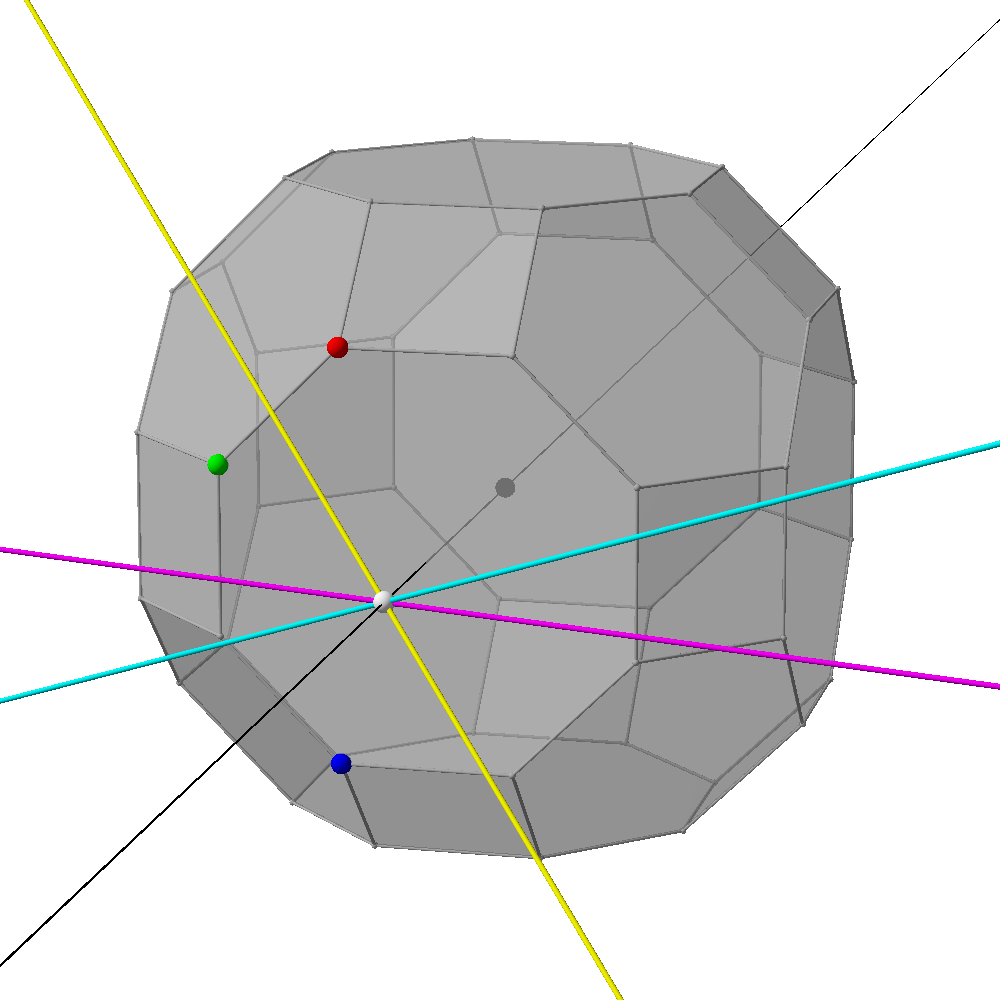
I have the strange problem, that the intersection of planes in SymPy works with simple examples, but fails for one with more complicated coordinates. I post both a simple example that works, and the one that fails. As the Povray images show, I have three planes that go through vertices of a polyhedron and are perpendicular to the line through the respective vertex and the center. I would like to calculate the point where these planes intersect, but SymPy gives wrong results for the lines in which pairs of planes intersect. In the images the correct intersections can be seen as short lines (created with CSG intersection). The long lines parallel to them are the ones calculated by SymPy.

Am I doing something wrong, or is this a bug in SymPy?

More images are here: http://paste.watchduck.net/1712/sympy_planes/
Does anyone know how to put many images on a page, without being kept from posting the question? ("Your post appears to contain code that is not properly formatted as code.")

Works

Code:

from sympy import Point3D, Plane


pointR = Point3D(1/2, 0, 1/2)
pointG = Point3D(1, 0, 0)

planeR = Plane(pointR, pointR)
planeG = Plane(pointG, pointG)

print('\n######## Intersection of the planes:')
lineRG = planeR.intersection(planeG)[0]  # yellow
print(lineRG)

print('\n######## Intersection of plane and contained line returns the line:')
lineRG_again = planeR.intersection(lineRG)[0]
print(lineRG_again.equals(lineRG))

Output:

######## Intersection of the planes:
Line3D(Point3D(1, 0, 0), Point3D(1, 1/2, 0))

######## Intersection of plane and contained line returns the line:
True

Fails

Code:

from sympy import sqrt, Point3D, Plane

pointR = Point3D(-1, 1 + sqrt(2), -2*sqrt(2) - 1)
pointG = Point3D(-sqrt(2) - 1, 1, -2*sqrt(2) - 1)
pointB = Point3D(-1, -sqrt(2) - 1, -2*sqrt(2) - 1)

planeR = Plane(pointR, pointR)
planeG = Plane(pointG, pointG)
planeB = Plane(pointB, pointB)

print('\n######## Intersections of the planes:')

lineRG = planeR.intersection(planeG)[0]  # yellow
lineRB = planeR.intersection(planeB)[0]  # magenta
lineGB = planeG.intersection(planeB)[0]  # cyan

print(lineRG)
print(lineRB)
print(lineGB)

print('\n######## Lines RG (yellow) and GB (cyan) intersect:')
print(lineRG.intersection(lineGB))
print('\n######## But line RB (magenta) is skew to both of them:')
print(lineRB.intersection(lineRG))
print(lineRB.intersection(lineGB))

print('\n######## Intersection of plane and contained line fails:')
lineRG_again = planeR.intersection(lineRG)

Output:

######## Intersections of the planes:
Line3D(Point3D(-1, 1, 0), Point3D((1 + sqrt(2))*(-2*sqrt(2) - 1) + 2*sqrt(2), -2*sqrt(2) + (-2*sqrt(2) - 1)*(-sqrt(2) - 1), -1 - (1 + sqrt(2))*(-sqrt(2) - 1)))
Line3D(Point3D(-1, 0, 0), Point3D((1 + sqrt(2))*(-2*sqrt(2) - 1) - (-2*sqrt(2) - 1)*(-sqrt(2) - 1) - 1, 0, 2 + 2*sqrt(2)))
Line3D(Point3D(-1, 1, 0), Point3D(-(-2*sqrt(2) - 1)*(-sqrt(2) - 1) - 2*sqrt(2) - 2, -(-2*sqrt(2) - 1)*(-sqrt(2) - 1) + 2 + 2*sqrt(2), 1 + (-sqrt(2) - 1)**2))

######## Lines RG (yellow) and GB (cyan) intersect:
[Point3D(-1, 1, 0)]

######## But line RB (magenta) is skew to both of them:
[]
[]

######## Intersection of plane and contained line fails:
Traceback (most recent call last):
  File "planes2.py", line 47, in <module>
    lineRG_again = planeR.intersection(lineRG)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/geometry/plane.py", line 390, in intersection
    p = a.subs(t, c[0])
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/core/basic.py", line 916, in subs
    rv = rv._subs(old, new, **kwargs)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/core/cache.py", line 93, in wrapper
    retval = cfunc(*args, **kwargs)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/core/basic.py", line 1030, in _subs
    rv = fallback(self, old, new)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/core/basic.py", line 1007, in fallback
    rv = self.func(*args)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/geometry/point.py", line 1104, in __new__
    args = Point(*args, **kwargs)
  File "/home/tilman/Code/024_polyhedron/env/lib/python3.5/site-packages/sympy/geometry/point.py", line 159, in __new__
    raise ValueError('Imaginary coordinates are not permitted.')
ValueError: Imaginary coordinates are not permitted.

Images:

Edit: Works with SymPy 1.1.2

After installing the development version of SymPy (pip install git+https://github.com/sympy/sympy.git) I get the correct results:

######## Intersections of pairs of planes:
Line3D(Point3D(-7 + sqrt(2)/2, -sqrt(2)/2 + 7, 0), Point3D((1 + sqrt(2))*(-2*sqrt(2) - 1) - 6 + 5*sqrt(2)/2, -5*sqrt(2)/2 + 6 + (-2*sqrt(2) - 1)*(-sqrt(2) - 1), -1 - (1 + sqrt(2))*(-sqrt(2) - 1)))
Line3D(Point3D(-13 - 6*sqrt(2), 0, 0), Point3D(-13 + (1 + sqrt(2))*(-2*sqrt(2) - 1) - (-2*sqrt(2) - 1)*(-sqrt(2) - 1) - 6*sqrt(2), 0, 2 + 2*sqrt(2)))
Line3D(Point3D(-13/2 - 3*sqrt(2), -7*sqrt(2)/2 + 1/2, 0), Point3D(-(-2*sqrt(2) - 1)*(-sqrt(2) - 1) - 15/2 - 5*sqrt(2), -(-2*sqrt(2) - 1)*(-sqrt(2) - 1) - 3*sqrt(2)/2 + 3/2, 1 + (-sqrt(2) - 1)**2))

######## Intersection of all planes:
[Point3D(0, 0, -20*sqrt(2)/7 - 11/7)]

Liverpudlian

Answer 1

In SymPy 1.1.1 and earlier versions, intersection returns wrong results when the normal vector involves a radical. Here is a simpler example:

p1 = Plane((1, 0, 0), (sqrt(2), 0, 0))
p2 = Plane((1, 1, 1), (1, 1, 1))
line = p1.intersection(p2)[0]      # this line is wrong
print(line.arbitrary_point())

This returns parametric equations of the line as Point3D(3, -sqrt(2)*t, sqrt(2)*t) which is wrong, since the first plane has equation sqrt(2)*(x-1) = 0, i.e., x=1.

You can still find the correct equations of intersection with

solve([p1.equation(), p2.equation()])

but this won't be as easy to use for plotting.

Good news

The bug (which was in linsolve method) is fixed in the current development version, 1.1.2.dev. Get it from GitHub repo.

Workaround for earlier versions

Replace radicals with floats:

pointR = Point3D(-1, N(1 + sqrt(2)), N(-2*sqrt(2) - 1))
pointG = Point3D(N(-sqrt(2) - 1), 1, N(-2*sqrt(2) - 1))
pointB = Point3D(-1, N(-sqrt(2) - 1), N(-2*sqrt(2) - 1))

This will not make everything perfect, but the impact of the bug should be diminished and you may be able to get reasonable intersections for your diagram.

Macaroon

Answer 2

This bug is not completely resolved on the version being developed. In particular concerning the intersections between the lines and circles of non simple coordinates. You can use shapely instead:

[What is most efficient way to find the intersection of a line and a circle in python?

Holds