Lowpass filter with a time-varying cutoff frequency, with Python

Question

How to apply a lowpass filter, with cutoff frequency varying linearly (or with a more general curve than linear) from e.g. 10000hz to 200hz along time, with numpy/scipy and possibly no other library?

Example:

• at 00:00,000, lowpass cutoff = 10000hz
• at 00:05,000, lowpass cutoff = 5000hz
• at 00:09,000, lowpass cutoff = 1000hz
• then cutoff stays at 1000hz during 10 seconds, then cutoff decreases down to 200hz

Here is how to do a simple 100hz lowpass:

from scipy.io import wavfile
import numpy as np
from scipy.signal import butter, lfilter

sr, x = wavfile.read('test.wav')
b, a = butter(2, 100.0 / sr, btype='low')  # Butterworth
y = lfilter(b, a, x)
wavfile.write('out.wav', sr, np.asarray(y, dtype=np.int16))

but how to make the cutoff vary?

Note: I've already read Applying time-variant filter in Python but the answer is quite complex (and it applies to many kinds of filter in general).

Cymoid

Always a 2nd order butterworth? – Yates

@StephenRauch Any IIR or FIR is ok, as long as the cutoff C(t) can vary smoothly along the time t (i.e. C(t) is not a piecewise constant function). – Cymoid

Sounds like a job for wavelet transforms, but I'm not experienced enough with them to give a good answer. Unfortuately pywavelets and pywt seem to be sort of dead tags. – Loathly

What is the initial sampling rate? – Loathly

@DanielF 44.1 Khz or 48 Khz or 96 Khz are typical values for which this would be useful. – Cymoid

Answer 1

One comparatively easy method is to keep the filter fixed and modulate signal time instead. For example, if signal time runs 10x faster a 10KHz lowpass will act like a 1KHz lowpass in standard time.

To do this we need to solve a simple ODE

dy       1
--  =  ----
dt     f(y)

Here t is modulated time y real time and f the desired cutoff at time y.

Prototype implementation:

from __future__ import division
import numpy as np
from scipy import integrate, interpolate
from scipy.signal import butter, lfilter, spectrogram

slack_l, slack = 0.1, 1
cutoff = 50
L = 25

from scipy.io import wavfile
sr, x = wavfile.read('capriccio.wav')
x = x[:(L + slack) * sr, 0]
x = x

# sr = 44100
# x = np.random.normal(size=((L + slack) * sr,))

b, a = butter(2, 2 * cutoff / sr, btype='low')  # Butterworth

# cutoff function
def f(t):
    return (10000 - 1000 * np.clip(t, 0, 9) - 1000 * np.clip(t-19, 0, 0.8)) \
        / cutoff

# and its reciprocal
def fr(_, t):
    return cutoff / (10000 - 1000 * t.clip(0, 9) - 1000 * (t-19).clip(0, 0.8))

# modulate time
# calculate upper end of td first
tdmax = integrate.quad(f, 0, L + slack_l, points=[9, 19, 19.8])[0]
span = (0, tdmax)
t = np.arange(x.size) / sr
tdinfo = integrate.solve_ivp(fr, span, np.zeros((1,)),
                             t_eval=np.arange(0, span[-1], 1 / sr),
                             vectorized=True)
td = tdinfo.y.ravel()
# modulate signal
xd = interpolate.interp1d(t, x)(td)
# and linearly filter
yd = lfilter(b, a, xd)
# modulate signal back to linear time
y = interpolate.interp1d(td, yd)(t[:-sr*slack])

# check
import pylab
xa, ya, z = spectrogram(y, sr)
pylab.pcolor(ya, xa, z, vmax=2**8, cmap='nipy_spectral')
pylab.savefig('tst.png')

wavfile.write('capriccio_vandalized.wav', sr, y.astype(np.int16))

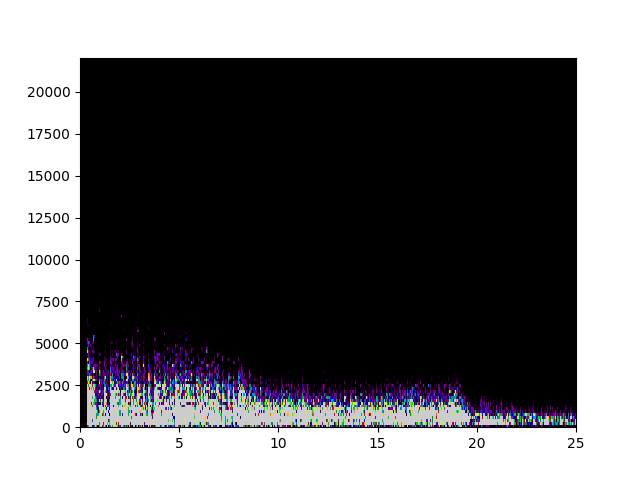
Sample output:

Spectrogram of first 25 seconds of BWV 826 Capriccio filtered with a time varying lowpass implemented via time bending.

Osbert

Thank you for your answer. When we're working on audio, making a signal run 10 times faster and then reslowing it will be heavily destructive (that would be similar to a 44.1 Khz => 4.1 Khz => 44.1 Khz resampling). If we apply a 1000 Hz lowpass anyway, it might not be too much of a problem, but in general this method wouldn't apply to a more general time-varying filter (example: you want to do the same as the original question, but with highpass or passband! then this solution would be too much destructive) – Cymoid

@Cymoid Three things: (1) your question as it stands is specifically about lowpass. (2) even if it weren't I think your concern can be resolved by either (a) fixing the filter at its lowest. Then only slowing down, i.e. upsampling of the signal would happen or (b) upsampling the signal before everything else or (c) a combination of (a) and (b) (equivalently (a) but fixing the filter even slower by a safety factor) (3) a bandpass with independently varying cutoffs could be done by applying the method twice. – Osbert

You're right about your remarks @PaulPanzer. Still, in the context of audio, resampling is a very very critical thing to do (even if done once, and even for close sampling rates 48 Khz => 44.1 khz), creating aliasing or other artefacts, etc., and requiring specific tools (there are lots of deep studies about that, and one of the most popular solutions nowadays is this library: mega-nerd.com/SRC). That's the reason why I preferred to not require such a destructive tool, just to apply a highpass or lowpass. – Cymoid

@Cymoid I may be wrong here but can't you just make the safety factor in (2c) so large that you are losing virtually no information? Aliasing should not be a problem since at the very end we are going back to the original time grid. It then becomes a question of computational cost. At some point brute forcing it by multiplying with a sparse total_no_samples x total_no_samples matrix might actually become cheaper. – Osbert

Here is the audio result of your code applied on Bach's Golbberg variations: gget.it/8sqvn/out.wav. As you can see, it's rather distorded (but not filtered!)... Yes Gould ;) – Cymoid

@Cymoid I've updated the code with (2c) and applied it to an example. To my untrained ear it sounds ok, and it definitely does filter, see spectrogram. I don't know how to paste audio; but the code should in theory run on any >25 sec 16 bit 44.1 kHz wav file you may choose to choose. – Osbert

@Cymoid I've uploaded the filtered audio here expirebox.com/download/4b9d2486abb784bc5a887430c83db977.html. It will expire after two days. (I feel I should mention that I don't know this hoster (just googled it), so I cannot guarantee it's safe.) – Osbert

@PaulPanzer, very interesting technique. – Yates

Answer 2

you can use scipy.fftpack.fftfreq and scipy.fftpack.rfft to set thresholds

fft = scipy.fftpack.fft(sound)
freqs = scipy.fftpack.fftfreq(sound.size, time_step)

for the time_step I did twice the sampling rate of the sound

fft[(freqs < 200)] = 0

this would set all set all frequencies less than 200 hz to zero

for the time varying cut off, I'd split the sound and apply the filters then. assuming the sound has a sampling rate of 44100, the 5000hz filter would start at sample 220500 (five seconds in)

10ksound = sound[:220500]
10kfreq = scipy.fftpack.fftreq(10ksound.size, time_step)
10kfft = scipy.fftpack.fft(10ksound)
10kfft[(10kfreqs < 10000)] = 0

then for the next filter:

5ksound = sound[220500:396900]
5kfreq = scipy.fftpack.fftreq(10ksound.size, time_step)
5kfft = scipy.fftpack.fft(10ksound)
5kfft[(5kfreqs < 5000)] = 0

etc

edit: to make it "sliding" or a gradual filter instead of piece wise, you could make the "pieces" much smaller and apply increasingly bigger frequency thresholds to the corresponding piece(5000 -> 5001 -> 5002)

Alie

Thanks for your answer, a few remarks: 1) Zeroing bins is not very good to do a filtering (but it kind of works), see DSP topics about this, 2) Lowpass means we keep the low frequencies and remove the higher freqs (you have done the contrary, this can easily be fixed). Biggest problem: 3) your filter is in fact 2 or 3 standard filters on each part of the sound. You have a "piece-wise constant cutoff" which is easy. The difficulty is having a "sliding" cutoff (see question). – Cymoid

You're right, doing it on small blocks (for example 1024 samples, i.e. ~23ms at 44.1Khz sampling rate) makes it work in the "sliding case": https://mcmap.net/q/1019544/-continuity-issue-when-applying-an-iir-filter-on-successive-time-frames. The important part is to care about the initial condition parameter. – Cymoid