python statsmodels: Help using ARIMA model for time series

ARIMA from statsmodels is giving me inaccurate answers for my output. I was wondering whether someone could help me understand what's wrong with my code.

This is a sample:

import pandas as pd
import numpy as np
import datetime as dt
from statsmodels.tsa.arima_model import ARIMA

# Setting up a data frame that looks twenty days into the past,
# and has linear data, from approximately 1 through 20
counts = np.arange(1, 21) + 0.2 * (np.random.random(size=(20,)) - 0.5)
start = dt.datetime.strptime("1 Nov 01", "%d %b %y")
daterange = pd.date_range(start, periods=20)
table = {"count": counts, "date": daterange}
data = pd.DataFrame(table)
data.set_index("date", inplace=True)

print data

               count
date
2001-11-01   0.998543
2001-11-02   1.914526
2001-11-03   3.057407
2001-11-04   4.044301
2001-11-05   4.952441
2001-11-06   6.002932
2001-11-07   6.930134
2001-11-08   8.011137
2001-11-09   9.040393
2001-11-10  10.097007
2001-11-11  11.063742
2001-11-12  12.051951
2001-11-13  13.062637
2001-11-14  14.086016
2001-11-15  15.096826
2001-11-16  15.944886
2001-11-17  17.027107
2001-11-18  17.930240
2001-11-19  18.984202
2001-11-20  19.971603

The rest of the code sets up the ARIMA model.

# Setting up ARIMA model
order = (2, 1, 2)
model = ARIMA(data, order, freq='D')
model = model.fit()
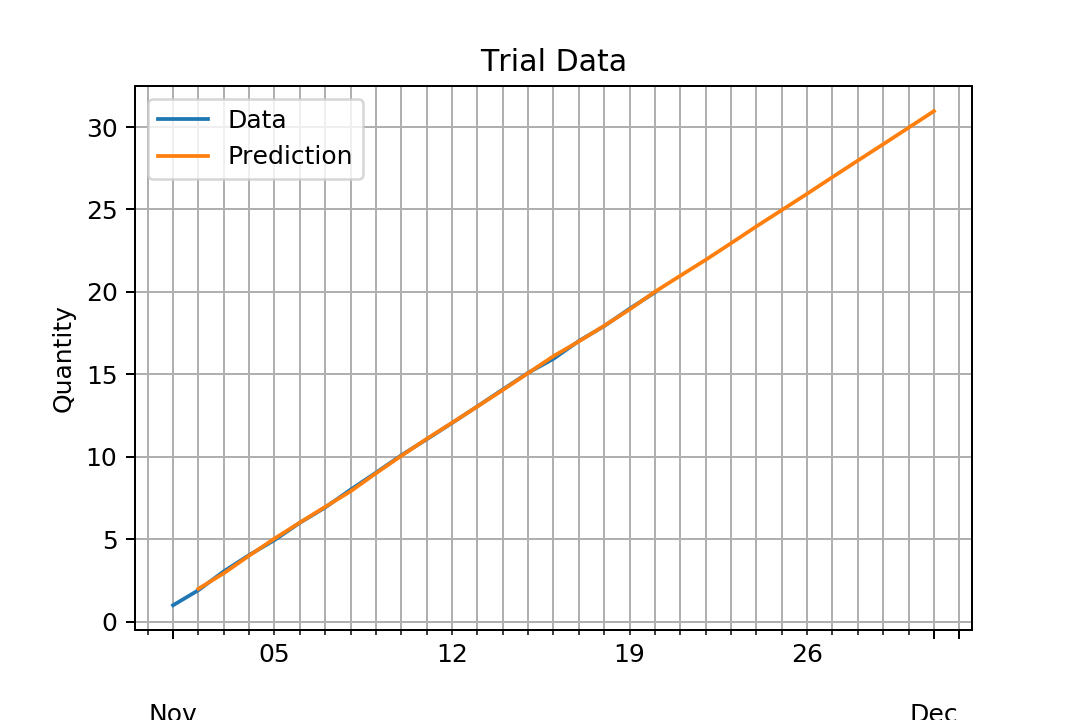
print model.predict(1, 20)

2001-11-02    1.006694
2001-11-03    1.056678
2001-11-04    1.116292
2001-11-05    1.049992
2001-11-06    0.869610
2001-11-07    1.016006
2001-11-08    1.110689
2001-11-09    0.945190
2001-11-10    0.882679
2001-11-11    1.139272
2001-11-12    1.094019
2001-11-13    0.918182
2001-11-14    1.027932
2001-11-15    1.041074
2001-11-16    0.898727
2001-11-17    1.078199
2001-11-18    1.027331
2001-11-19    0.978840
2001-11-20    0.943520
2001-11-21    1.040227
Freq: D, dtype: float64

As you could see, the data is just constant around 1 instead of increasing. What am I doing wrong here?

(On a side note, I can't pass in string dates like "2001-11-21" into the predict function for some reason. It would be helpful to know why.)

TL;DR

The way you use predict returns a linear prediction in terms of the differenced endogenous variable not a prediction of the levels of the original endogenous variable.

You must feed predict method with typ='levels' to change this behavior:

preds = fit.predict(1, 30, typ='levels')

See documentation of ARIMAResults.predict for details.

Step by step

Dataset

We load data you provided in your MCVE:

import io
import pandas as pd

raw = io.StringIO("""date        count
2001-11-01   0.998543
2001-11-02   1.914526
2001-11-03   3.057407
2001-11-04   4.044301
2001-11-05   4.952441
2001-11-06   6.002932
2001-11-07   6.930134
2001-11-08   8.011137
2001-11-09   9.040393
2001-11-10  10.097007
2001-11-11  11.063742
2001-11-12  12.051951
2001-11-13  13.062637
2001-11-14  14.086016
2001-11-15  15.096826
2001-11-16  15.944886
2001-11-17  17.027107
2001-11-18  17.930240
2001-11-19  18.984202
2001-11-20  19.971603""")

data = pd.read_fwf(raw, parse_dates=['date'], index_col='date')

As we may expect data are auto-correlated:

from pandas.plotting import autocorrelation_plot
autocorrelation_plot(data)

Model & Training

We create an ARIMA Model object for a given setup (P,D,Q) and we train it on our data using the fit method:

from statsmodels.tsa.arima_model import ARIMA

order = (2, 1, 2)
model = ARIMA(data, order, freq='D')
fit = model.fit()

It returns an ARIMAResults object which is matter of interest. We can check out the quality of our model:

fit.summary()

                            ARIMA Model Results                              
==============================================================================
Dep. Variable:                D.count   No. Observations:                   19
Model:                 ARIMA(2, 1, 2)   Log Likelihood                  25.395
Method:                       css-mle   S.D. of innovations              0.059
Date:                Fri, 18 Jan 2019   AIC                            -38.790
Time:                        07:54:36   BIC                            -33.123
Sample:                    11-02-2001   HQIC                           -37.831
                         - 11-20-2001                                         
==============================================================================
                  coef    std err          z      P>|z|      [0.025     0.975]
------------------------------------------------------------------------------
const           1.0001      0.014     73.731      0.000       0.973      1.027
ar.L1.D.count  -0.3971      0.295     -1.346      0.200      -0.975      0.181
ar.L2.D.count  -0.6571      0.230     -2.851      0.013      -1.109     -0.205
ma.L1.D.count   0.0892      0.208      0.429      0.674      -0.318      0.496
ma.L2.D.count   1.0000      0.640      1.563      0.140      -0.254      2.254
                                    Roots                                    
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -0.3022           -1.1961j            1.2336           -0.2894
AR.2            -0.3022           +1.1961j            1.2336            0.2894
MA.1            -0.0446           -0.9990j            1.0000           -0.2571
MA.2            -0.0446           +0.9990j            1.0000            0.2571
------------------------------------------------------------------------------

And we can roughly estimate how residuals are distributed:

residuals = pd.DataFrame(fit.resid, columns=['residuals'])
residuals.plot(kind='kde')

Prediction

If we are satisfied with our model, then we can predict some in-sample or out-sample data.

This can be done with the predict method which by default returns the differenced endogenous variable not the endogenous variable itself. To change this behavior, we must specify typ='levels':

preds = fit.predict(1, 30, typ='levels')

Then our predictions do have the same levels of our training data:

Additionally, if we are interested to also have confidence intervals, then we can use the forecast method.

String Argument

It is also possible to feed predict with strings (always use the ISO-8601 format if you want to avoid troubles) or datetime objects:

preds = fit.predict("2001-11-02", "2001-12-15", typ='levels')

Works as expected on StatsModels 0.9.0:

import statsmodels as sm
sm.__version__ # '0.9.0'