MATLAB: Find abbreviated version of matrix that minimises sum of matrix elements

Question

I have a 151-by-151 matrix A. It's a correlation matrix, so there are 1s on the main diagonal and repeated values above and below the main diagonal. Each row/column represents a person.

For a given integer n I will seek to reduce the size of the matrix by kicking people out, such that I am left with a n-by-n correlation matrix that minimises the total sum of the elements. In addition to obtaining the abbreviated matrix, I also need to know the row number of the people who should be booted out of the original matrix (or their column number - they'll be the same number).

As a starting point I take A = tril(A), which will remove redundant off-diagonal elements from the correlation matrix.

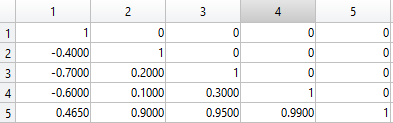
So, if n = 4 and we have the hypothetical 5-by-5 matrix above, it's very clear that person 5 should be kicked out of the matrix, since that person is contributing a lot of very high correlations.

It's also clear that person 1 should not be kicked out, since that person contributes a lot of negative correlations, and thus brings down the sum of the matrix elements.

I understand that sum(A(:)) will sum everything in the matrix. However, I'm very unclear about how to search for the minimum possible answer.

I noticed a similar question Finding sub-matrix with minimum elementwise sum, which has a brute force solution as the accepted answer. While that answer works fine there it's impractical for a 151-by-151 matrix.

EDIT: I had thought of iterating, but I don't think that truly minimizes the sum of elements in the reduced matrix. Below I have a 4-by-4 correlation matrix in bold, with sums of rows and columns on the edges. It's apparent that with n = 2 the optimal matrix is the 2-by-2 identity matrix involving Persons 1 and 4, but according to the iterative scheme I would have kicked out Person 1 in the first phase of iteration, and so the algorithm makes a solution that is not optimal. I wrote a program that always generated optimal solutions, and it works well when n or k are small, but when trying to make an optimal 75-by-75 matrix from a 151-by-151 matrix I realised my program would take billions of years to terminate.

I vaguely recalled that sometimes these n choose k problems can be resolved with dynamic programming approaches that avoid recomputing things, but I can't work out how to solve this, and nor did googling enlighten me.

I'm willing to sacrifice precision for speed if there's no other option, or the best program will take more than a week to generate a precise solution. However, I'm happy to let a program run for up to a week if it will generate a precise solution.

If it's not possible for a program to optimise the matrix within an reasonable timeframe, then I would accept an answer that explains why n choose k tasks of this particular sort can't be resolved within reasonable timeframes.

Smearcase

sum(A, 2) returns the sum of each row. – Houdon

Are you able to expand on how that code can help find the n-by-n abbreviated version of the matrix that minimises the sum of the matrix elements? – England

Let me see if I understand the question precisely. The problem is to choose a vector x to minimize x'*S*x where S is a given symmetric, positive definite matrix and x is subject to the constraints that the entries of x are either 1 or 0 and the elements of x sum to n. Correct? – Paronychia

This link may be helpful. Also, how willing are you to sacrifice precision for speed? – Paronychia

I edited the OP to clarify the precision vs speed issue. Your understanding of the question is correct, except that S is a correlation matrix, and thus is necessarily positive semidefinite and not necessarily positive definite. – England

Have you looked into genetic algorithms, if you want I can give you some hints in that direction. – Wimberly

So far I have not tried genetic algorithms. I welcome further suggestions about how to proceed. – England

This can be transformed into a maximum cut problem. Given that your problem is 151x151, this exact solver may be able to handle it. If not, you can instead write a very fast implementation of simulated annealing or tabu search. – Anorthosite

Answer 1

Working on a suggestion from Matthew Gunn and also some advice at the Gurobi forums, I came up with the following function. It seems to work pretty well.

I will award it the answer, but if someone can come up with code that works better I'll remove the tick from this answer and place it on their answer instead.

function [ values ] = the_optimal_method( CM , num_to_keep)
%the_iterative_method Takes correlation matrix CM and number to keep, returns list of people who should be kicked out 

N = size(CM,1);  

clear model;  
names = strseq('x',[1:N]);  
model.varnames = names;  
model.Q = sparse(CM); % Gurobi needs a sparse matrix as input  
model.A = sparse(ones(1,N));  
model.obj = zeros(1,N);  
model.rhs = num_to_keep;  
model.sense = '=';  
model.vtype = 'B';

gurobi_write(model, 'qp.mps');

results = gurobi(model);

values = results.x;

end

Smearcase

Answer 2

There are several approaches to finding an approximate solution (eg. quadratic programming on relaxed problem or greedy search), but finding the exact solution is an NP-hard problem.

Disclaimer: I'm not an expert on binary quadratic programming, and you may want to consult the academic literature for more sophisticated algorithms.

Mathematically equivalent formulation:

Your problem is equivalent to:

For some symmetric, positive semi-definite matrix S

minimize (over vector x)  x'*S*x

             subject to     0 <= x(i) <= 1        for all i
                            sum(x)==n
                            x(i) is either 1 or 0 for all i

This is a quadratic programming problem where the vector x is restricted to taking only binary values. Quadratic programming where the domain is restricted to a set of discrete values is called mixed integer quadratic programming (MIQP). The binary version is sometimes called Binary Quadratic Programming (BQP). The last restriction, that x is binary, makes the problem substantially more difficult; it destroys the problem's convexity!

Quick and dirty approach to finding an approximate answer:

If you don't need a precise solution, something to play around with might be a relaxed version of the problem: drop the binary constraint. If you drop the constraint that x(i) is either 1 or 0 for all i, then the problem becomes a trivial convex optimization problem and can be solved nearly instantaneously (eg. by Matlab's quadprog). You could try removing entries that, on the relaxed problem, quadprog assigns the lowest values in the x vector, but this does not truly solve the original problem!

Note also that the relaxed problem gives you a lower bound on the optimal value of the original problem. If your discretized version of the solution to the relaxed problem leads to a value for the objective function close to the lower bound, there may be a sense in which this ad-hoc solution can't be that far off from the true solution.

---

To solve the relaxed problem, you might try something like:

% k is number of observations to drop
n = size(S, 1);
Aeq = ones(1,n)
beq = n-k;
[x_relax, f_relax] = quadprog(S, zeros(n, 1), [], [], Aeq, beq, zeros(n, 1), ones(n, 1));
f_relax = f_relax * 2;  % Quadprog solves .5 * x' * S * x... so mult by 2
temp = sort(x_relax);
cutoff = temp(k);
x_approx = ones(n, 1);
x_approx(x_relax <= cutoff) = 0;
f_approx = x_approx' * S * x_approx;

I'm curious how good x_approx is? This doesn't solve your problem, but it might not be horrible! Note that f_relax is a lower bound on the solution to the original problem.

---

Software to solve your exact problem

You should check out this link and go down to the section on Mixed Integer Quadratic Programming (MIQP). It looks to me that Gurobi can solve problems of your type. Another list of solvers is here.

Paronychia

It's true that the problem is equivalent to what you just stated, aside from one thing. Correlation matrices are semipositive definite and not positive definite. See, for instance, stats.stackexchange.com/questions/182875/…. Does that change things? – England

@user1205901 basically same deal. You can get a zero eigenvalue (hence semi-definite rather than definite) if some linear combination of random variables is perfectly correlated with another. – Paronychia

Is there a typo in 0 <= x(i) <= 1 for all i? It's the elements in S that have to be between 0 and 1, whereas the elements in x have to be either 0 or 1. – England

In your problem, x(i) has to be either 1 or 0. In the relaxed problem, it has to be BETWEEN 1 and 0, inclusive. Eg. you allow x(i) to take the value .4 or .3 . Anything between 0 and 1 is allowed in the relaxed problem! The relaxed problem gives you back a vector x of doubles. – Paronychia

Can you explain why the problem is NP-hard? I can only prove NP-hardness if the positive semidefiniteness constraint is relaxed, in which case there's a straightforward reduction from the maximum clique problem. – Lax

It's been a long time since I did complexity theory. I'm just saying I think it's NP-hard because I read somewhere that binary quadratic programming is NP hard, but I'm not knowledgable enough about this area to know if there are qualifications/exceptions. If you drop the binary constraint, the problem can be solved about instantly. – Paronychia

@MatthewGunn What's the purpose of including both the specification 0 <= x(i) <= 1 for all i and the specification x(i) is either 1 or 0 for all i? Doesn't the first specification apply if we're taking a relaxed approach, and the second apply if we're taking the strict (binary constraint) approach? – England

clearly the first is redundant if you have the last one. I just put it in there so I could CLEANLY argue the latter problem is simply a less constrained version of the former. – Paronychia

I'm not sure how best to judge whether x_approx is horrible or somewhat reasonable. However, on my first attempt with random data it made a mistake. I gave it the correlation matrix from pastebin.com/MiLJnkvr, with k=2 and it wanted to kick out the fourth and fifth rows. Kicking out the fifth row is correct. However, the fourth row sums to 1.22, which is less than the first row's 1.25. – England

Checkout my link go Gurobi yet? This may be what you want. And what do you say the solution is to the one in pastebin? I think [1;1;1;0;0] is the solution to the S matrix you posted in patebin. – Paronychia

You are right that [1;1;1;0;0] is the solution to the S matrix I posted in pastebin. I'd incorrectly thought it was [0;1;1;1;0]. I'll check out Gurobi. – England

I haven't worked out how to use Gurobi yet, but I wrote a script at pastebin.com/e84dtxgy to compare the iterative method versus x_approx. It seems like they're usually equivalent, but x_approx occasionally does worse. – England

Answer 3

This is an approximate solution using a genetic algorithm.

I started with your test case:

data_points = 10; % How many data points will be generated for each person, in order to create the correlation matrix.
num_people = 25; % Number of people initially.
to_keep = 13; % Number of people to be kept in the correlation matrix.
to_drop = num_people - to_keep; % Number of people to drop from the correlation matrix.
num_comparisons = 100; % Number of times to compare the iterative and optimization techniques.
for j = 1:data_points
    rand_dat(j,:) = 1 + 2.*randn(num_people,1); % Generate random data.
end
A = corr(rand_dat);

then I defined the functions you need to evolve the genetic algorithm:

function individuals = user1205901individuals(nvars, FitnessFcn, gaoptions, num_people)

individuals = zeros(num_people,gaoptions.PopulationSize);
for cnt=1:gaoptions.PopulationSize
    individuals(:,cnt)=randperm(num_people);
end

individuals = individuals(1:nvars,:)';

is the individual generation function.

function fitness = user1205901fitness(ind, A)

fitness = sum(sum(A(ind,ind)));

is the fitness evaluation function

function offspring = user1205901mutations(parents, options, nvars, FitnessFcn, state, thisScore, thisPopulation, num_people)

offspring=zeros(length(parents),nvars);
for cnt=1:length(parents)
    original = thisPopulation(parents(cnt),:);
    extraneus = setdiff(1:num_people, original);
    original(fix(rand()*nvars)+1) = extraneus(fix(rand()*(num_people-nvars))+1);
    offspring(cnt,:)=original;
end

is the function to mutate an individual

function children = user1205901crossover(parents, options, nvars, FitnessFcn, unused, thisPopulation)

children=zeros(length(parents)/2,nvars);
cnt = 1;
for cnt1=1:2:length(parents)
    cnt2=cnt1+1;
        male = thisPopulation(parents(cnt1),:);
        female = thisPopulation(parents(cnt2),:);
        child = union(male, female);
        child = child(randperm(length(child)));
        child = child(1:nvars);
        children(cnt,:)=child;
        cnt = cnt + 1;

end

is the function to generate a new individual coupling two parents.

At this point you can define your problem:

gaproblem2.fitnessfcn=@(idx)user1205901fitness(idx,A)
gaproblem2.nvars = to_keep
gaproblem2.options = gaoptions()
gaproblem2.options.PopulationSize=40
gaproblem2.options.EliteCount=10
gaproblem2.options.CrossoverFraction=0.1
gaproblem2.options.StallGenLimit=inf
gaproblem2.options.CreationFcn= @(nvars,FitnessFcn,gaoptions)user1205901individuals(nvars,FitnessFcn,gaoptions,num_people)
gaproblem2.options.CrossoverFcn= @(parents,options,nvars,FitnessFcn,unused,thisPopulation)user1205901crossover(parents,options,nvars,FitnessFcn,unused,thisPopulation)
gaproblem2.options.MutationFcn=@(parents, options, nvars, FitnessFcn, state, thisScore, thisPopulation) user1205901mutations(parents, options, nvars, FitnessFcn, state, thisScore, thisPopulation, num_people)
gaproblem2.options.Vectorized='off'

open the genetic algorithm tool

gatool

from the File menu select Import Problem... and choose gaproblem2 in the window that opens.

Now, run the tool and wait for the iterations to stop.

The gatool enables you to change hundreds of parameters, so you can trade speed for precision in the selected output.

The resulting vector is the list of indices that you have to keep in the original matrix so A(garesults.x,garesults.x) is the matrix with only the desired persons.

Wimberly

Answer 4

If I have understood you problem statement, you have a N x N matrix M (which happens to be a correlation matrix), and you wish to find for integer n where 2 <= n < N, a n x n matrix m which minimises the sum over all elements of m which I denote f(m)?

In Matlab it is fairly easy and fast to obtain a sub-matrix of a matrix (see for example Removing rows and columns from matrix in Matlab), and the function f is relatively inexpensive to evaluate for n = 151. So why can't you implement an algorithm that solves this backwards dynamically in a program as below where I have sketched out the pseudocode:

function reduceM(M, n){

    m = M

    for (ii = N to n+1) {

        for (jj = 1 to ii) {

            val(jj) = f(m) where mhas column and row jj removed, f(X) being summation over all elements of X

        }

        JJ(ii) = jj s.t. val(jj) is smallest

        m = m updated by removing column and row JJ(ii)   
    }
}

In the end you end up with an m of dimension n which is the solution to your problem and a vector JJ which contains the indices removed at each iteration (you should easily be able to convert these back to indices applicable to the full matrix M)

Vulgar

This answer completely misunderstands the complexity of the problem. From the question, "I noticed a similar question 'Finding sub-matrix with minimum elementwise sum', which has a brute force solution as the accepted answer. While that answer works fine there it's impractical for a 151-by-151 matrix." If user wants to keep 140 rows/columns (eliminate 11), that involves nchoosek(151, 140) = approximately 10^29 different matrices to check! That doesn't work. ...solves this backwards dynamically... is vague. This question is a very hard problem, and this answer honestly does not help. – Paronychia

Appreciate your comment by the complexity you see comes from your chosen approach to the solution by seeing it as a combinatorial problem. – Vulgar

Where we differ is that I suggest we solve it through a backward induction approach. Given a matrix of size M, we can easily find the solution to the problem if we simply wish to reduce the dimension by 1, i.e. n = M -1. If we were to apply this process M - n times, we arrive at an answer that is optimal for n, and we get to record the removed "people" along the way. – Vulgar

No, that doesn't necessarily you give the answer!! Imagine two problems: (1) Reduce dimension by 1 or (2) Reduce the dimension by two. They can involve removing COMPLETELY different rows/columns. – Paronychia

If you understand my suggestion you will realise that we are not doing 10^29 checks of all possible solution matrix, but more like roughly x = 151+150+149... n times because at each iteration you have to examine as many number of possible solution as the dimension of the starting matrix – Vulgar

Write your code. Your greedy algorithm won't necessarily converge on the global optimum. Period. – Paronychia

Example where greedy fails: M = [1.0000, -0.3070, -0.8120, -0.3370; -0.3070, 1.0000, 0.4980 -0.4960;-0.8120, 0.4980,1.0000,0.4210; -0.3370,-0.4960 ,0.4210 ,1.0000]; If dropping one, you drop the 3rd row and column. If dropping two, it's optimal to drop the 2nd and fourth row and column. A greedy algorithm would drop rowcol = 3, then would be unable to find global optimum of dropping rowcol = 2,4. – Paronychia

I stand corrected. Matthew Gunn is right, my solution is incorrect. Please ingore. – Vulgar

No worries. The problem looks simple on its surface... Not until I started reading a bit did I realize it's surprisingly difficult! – Paronychia

That's why I love mathematics :) I still think there is a way to devise an efficient solution to this problem though and hope someone would come up with one! – Vulgar