What is the role of the bias in neural networks? [closed]

Question

I'm aware of the gradient descent and the back-propagation algorithm. What I don't get is: when is using a bias important and how do you use it?

For example, when mapping the AND function, when I use two inputs and one output, it does not give the correct weights. However, when I use three inputs (one of which is a bias), it gives the correct weights.

Anadem

Check out this question: https://mcmap.net/q/54483/-perceptron-learning-algorithm-not-converging-to-0 for an example of an actual problem where the OP was not using a bias term – Whitver

And here is a nice example in Python of why the bias is important :) #38249157 – Revis

here's a great article full of of backprop math, also covering bias updates: theclevermachine.wordpress.com/2014/09/06/… – Jacket

Answer 1

I think that biases are almost always helpful. In effect, a bias value allows you to shift the activation function to the left or right, which may be critical for successful learning.

It might help to look at a simple example. Consider this 1-input, 1-output network that has no bias:

The output of the network is computed by multiplying the input (x) by the weight (w₀) and passing the result through some kind of activation function (e.g. a sigmoid function.)

Here is the function that this network computes, for various values of w₀:

Changing the weight w₀ essentially changes the "steepness" of the sigmoid. That's useful, but what if you wanted the network to output 0 when x is 2? Just changing the steepness of the sigmoid won't really work -- you want to be able to shift the entire curve to the right.

That's exactly what the bias allows you to do. If we add a bias to that network, like so:

...then the output of the network becomes sig(w₀*x + w₁*1.0). Here is what the output of the network looks like for various values of w₁:

Having a weight of -5 for w₁ shifts the curve to the right, which allows us to have a network that outputs 0 when x is 2.

Downe

@user1621769: The simplest approach is a network with a single bias node that connects to all non-input nodes in the network. – Downe

would that be the most effective though? it seems to me that a bias unit at the output layer, or 1 per layer would make the prediction better. – Lipps

@user1621769: The main function of a bias is to provide every node with a trainable constant value (in addition to the normal inputs that the node recieves). You can achieve that with a single bias node with connections to N nodes, or with N bias nodes each with a single connection; the result should be the same. – Downe

@user1621769: You might be failing to take weightings into account? Each connection has a trainable weighting, and the bias node has a fixed value. – Unthoughtof

In case if I don't need to shift the curve to either left or right, then is it still necessary to add the bias unit or can I skip that? – Commiserate

@user132458 It's a little unusual to know such things about your desired solution, but I suppose you could skip it if you know the problem doesn't require it. – Downe

@user132458, if the training algorithm figures out that you don't need the bias shift, the bias weights will probably approach 0. Thus eliminating the bias signal. – Foudroyant

Then what is bias value for each node in neural network ? Is it the same thing as threshold value for each neuron ? Bcoz some people use bias keyword for each node as well having the number of bias nodes same as number of nodes in a layer. Since The BIAS NODE (for intercept) is only one for a layer as per above explanation... hence this doubt ! – Electrical

@NateKohl: I really like your answer, but you say something that sounds paradoxical to me: "a trainable constant value"... For me a constant value is a value that does not change. However you write trainable, which means this value is meant to change. So, is a bias constant, or trainable? – Majunga

@maikovich: Sorry -- I used 'constant' to differentiate the bias node's input (which doesn't change) from other input nodes (which receive input values that can vary). The weights coming out of the input/bias nodes are the trainable bits. Hope this helps. – Downe

If you see a neural network as a bunch of linear functions connected to non-linear neurons then you can see that the bias helps each linear function to fit better the data by fitting the function along the y-axis. – Fiddlestick

what would be a bias range? Is it also -1 to 1? – Nexus

In order for the layer to be a universal approximator, a bias with independent weights for each neuron is necessary, correct? – Proboscidean

@JuanCamiloZapata Doesn't the bias shift the function along the x-axis? – Proboscidean

@Gabriel: There should be one bias per hidden neuron. – Unstudied

@Lipps Their should be one bias per layer in network – Dope

@Dope we need 1 bias per neuron in order to have each sigmoid (for each neuron) shifted left or right. One bias for a whole layer would only shift all the sigmoids left or right at the same time during the learning. And that's not what we want. We want each neuron of a given layer to compete with the others in order to represent its own "knowledge". – Plate

The explanation is nice. How the output is 2 here. I can't figure it out. Please help – Phiphenomenon

Answer 2

A simpler way to understand what the bias is: it is somehow similar to the constant b of a linear function

y = ax + b

It allows you to move the line up and down to fit the prediction with the data better.

Without b, the line always goes through the origin (0, 0) and you may get a poorer fit.

Garda

nice anology but if we set the bias to 1 then why does it make difference to the fit now that every line will now go through (0,1) instead of (0,0)?As all lines are now biased to y=1 instead of y=0 why is this helpful? – Dollie

@Dollie Because by multiplying a bias by a weight, you can shift it by an arbitrary amount. – Manstopper

Is it correct to call b a "coefficient"? Isn't a "coefficient" a number used to multiply a variable? – Bounteous

b is not "coefficient" rather it is intercept. – Repine

b is the coefficient of $x^0$. a is the coefficient of $x^1$ – Grand

Yes! In particular, without a bias, 0 would be a fixed point for many neural nets (as 0 is also a fixed point for many activation functions). I.e. for input 0 the NN would always output 0 with no chance of learning to output a different value. – Hilton

Thanks for your answer - the top answer says it shifts it left and right? Can you please clarify? – Fluttery

@Fluttery If you think of a regular algebraic function like a parabola => f(x) = (x -a)^2 + c, then the a would shift the function left/right, while the c would shift it up and down. Technically, the above answer is more accurate since the bias is added before you use the activation function, so it would be shifting it left/right, but the general idea is still the same – Unicorn

Answer 3

Here are some further illustrations showing the result of a simple 2-layer feed forward neural network with and without bias units on a two-variable regression problem. Weights are initialized randomly and standard ReLU activation is used. As the answers before me concluded, without the bias the ReLU-network is not able to deviate from zero at (0,0).

Cassis

Can you please add the function that's plotted with axis labels? – Holley

Sorry, the points are just randomly chosen. There is no real function behind them. – Cassis

Can you share the code doing the animation? – Spirogyra

Are you still interested in this? What would be the best way to share code on stackoverflow? – Cassis

@JPK. share it as github link please – Biggin

here you go github.com/JaPhi/NN_autograd_bias – Cassis

Nice! This is a good illustration of how bias lets the model be more "flexible". – Corpulent

Answer 4

Two different kinds of parameters can be adjusted during the training of an ANN, the weights and the value in the activation functions. This is impractical and it would be easier if only one of the parameters should be adjusted. To cope with this problem a bias neuron is invented. The bias neuron lies in one layer, is connected to all the neurons in the next layer, but none in the previous layer and it always emits 1. Since the bias neuron emits 1 the weights, connected to the bias neuron, are added directly to the combined sum of the other weights (equation 2.1), just like the t value in the activation functions.1

The reason it's impractical is because you're simultaneously adjusting the weight and the value, so any change to the weight can neutralize the change to the value that was useful for a previous data instance... adding a bias neuron without a changing value allows you to control the behavior of the layer.

Furthermore the bias allows you to use a single neural net to represent similar cases. Consider the AND boolean function represented by the following neural network:

_{(source: aihorizon.com)}

• w0 corresponds to b.
• w1 corresponds to x1.
• w2 corresponds to x2.

A single perceptron can be used to represent many boolean functions.

For example, if we assume boolean values of 1 (true) and -1 (false), then one way to use a two-input perceptron to implement the AND function is to set the weights w0 = -3, and w1 = w2 = .5. This perceptron can be made to represent the OR function instead by altering the threshold to w0 = -.3. In fact, AND and OR can be viewed as special cases of m-of-n functions: that is, functions where at least m of the n inputs to the perceptron must be true. The OR function corresponds to m = 1 and the AND function to m = n. Any m-of-n function is easily represented using a perceptron by setting all input weights to the same value (e.g., 0.5) and then setting the threshold w0 accordingly.

Perceptrons can represent all of the primitive boolean functions AND, OR, NAND ( 1 AND), and NOR ( 1 OR). Machine Learning- Tom Mitchell)

The threshold is the bias and w0 is the weight associated with the bias/threshold neuron.

Lip

Think of it as a general rule of thumb: add bias! Neural networks are "unpredictable" to a certain extent so if you add a bias neuron you're more likely to find solutions faster then if you didn't use a bias. Of course this is not mathematically proven, but it's what I've observed in literature and in general use. – Lip

Answer 5

The bias is not an NN term. It's a generic algebra term to consider.

Y = M*X + C (straight line equation)

Now if C(Bias) = 0 then, the line will always pass through the origin, i.e. (0,0), and depends on only one parameter, i.e. M, which is the slope so we have less things to play with.

C, which is the bias takes any number and has the activity to shift the graph, and hence able to represent more complex situations.

In a logistic regression, the expected value of the target is transformed by a link function to restrict its value to the unit interval. In this way, model predictions can be viewed as primary outcome probabilities as shown:

Sigmoid function on Wikipedia

This is the final activation layer in the NN map that turns on and off the neuron. Here also bias has a role to play and it shifts the curve flexibly to help us map the model.

Ningsia

Answer 6

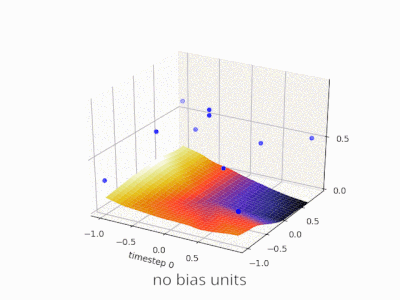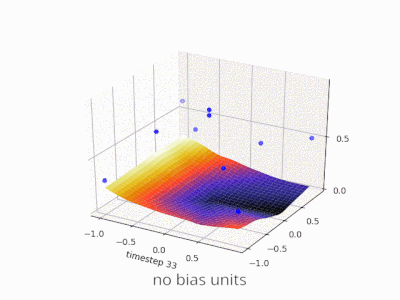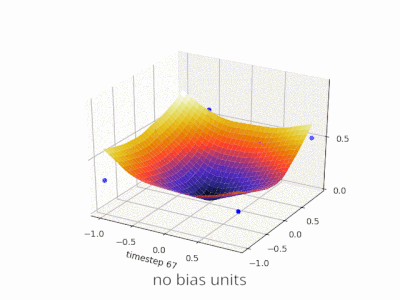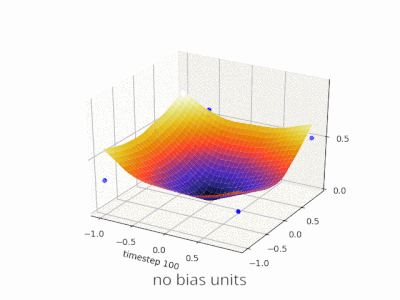
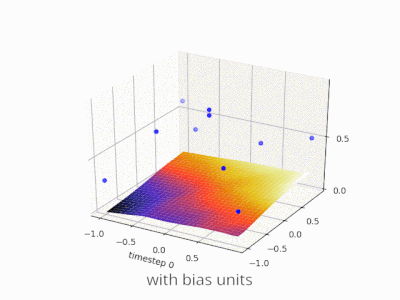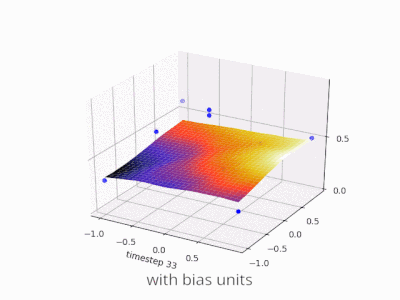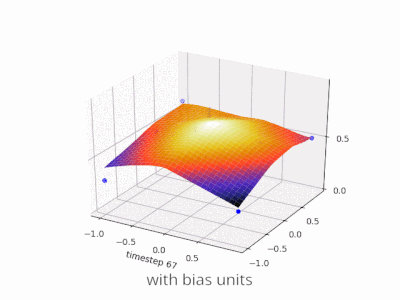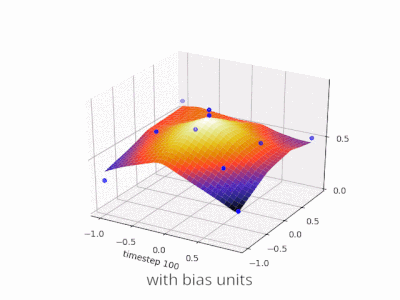
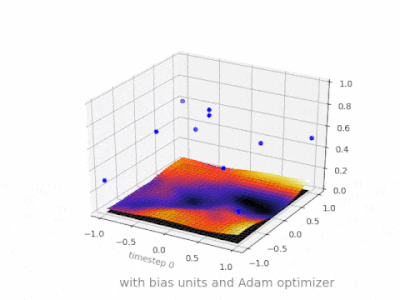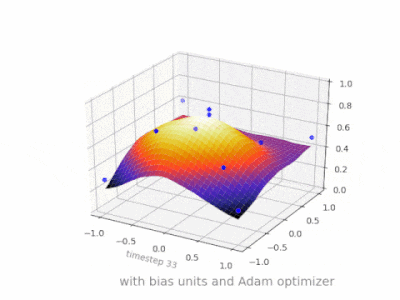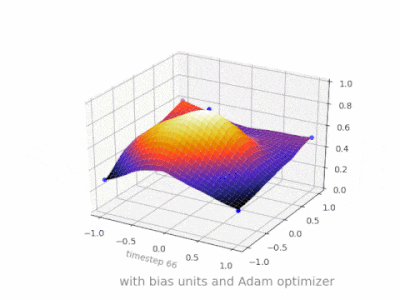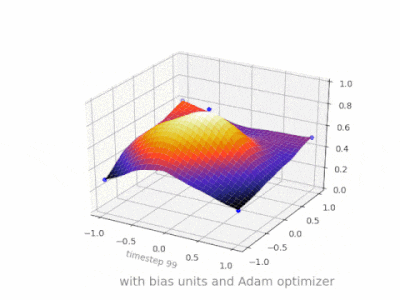
A layer in a neural network without a bias is nothing more than the multiplication of an input vector with a matrix. (The output vector might be passed through a sigmoid function for normalisation and for use in multi-layered ANN afterwards, but that’s not important.)

This means that you’re using a linear function and thus an input of all zeros will always be mapped to an output of all zeros. This might be a reasonable solution for some systems but in general it is too restrictive.

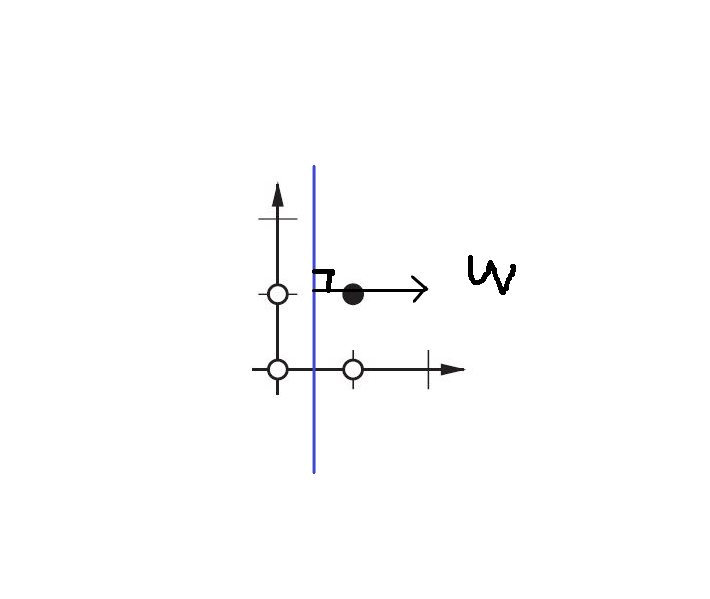
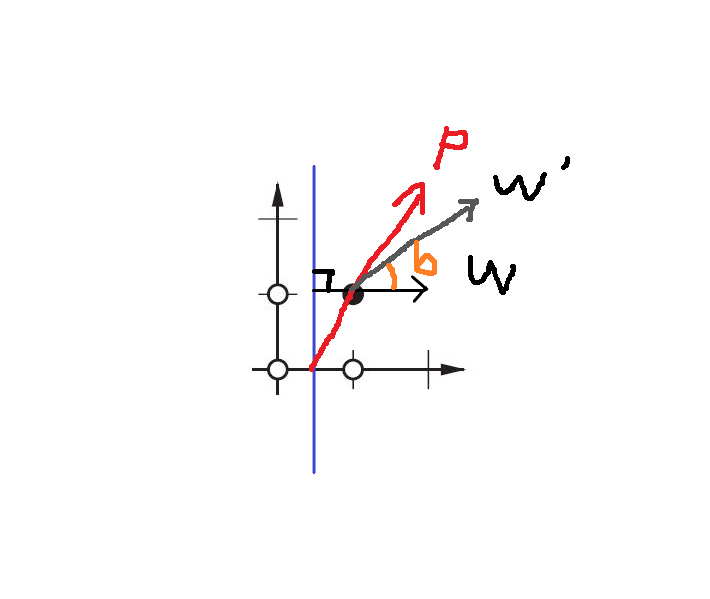
Using a bias, you’re effectively adding another dimension to your input space, which always takes the value one, so you’re avoiding an input vector of all zeros. You don’t lose any generality by this because your trained weight matrix needs not be surjective, so it still can map to all values previously possible.

2D ANN:

For a ANN mapping two dimensions to one dimension, as in reproducing the AND or the OR (or XOR) functions, you can think of a neuronal network as doing the following:

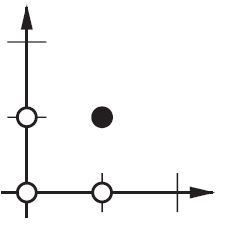
On the 2D plane mark all positions of input vectors. So, for boolean values, you’d want to mark (-1,-1), (1,1), (-1,1), (1,-1). What your ANN now does is drawing a straight line on the 2d plane, separating the positive output from the negative output values.

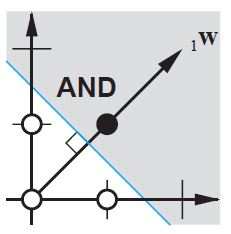
Without bias, this straight line has to go through zero, whereas with bias, you’re free to put it anywhere. So, you’ll see that without bias you’re facing a problem with the AND function, since you can’t put both (1,-1) and (-1,1) to the negative side. (They are not allowed to be on the line.) The problem is equal for the OR function. With a bias, however, it’s easy to draw the line.

Note that the XOR function in that situation can’t be solved even with bias.

Lisle

If you use a sigmoid transfer function, you introduce non-linearity. Stating that this is a linear function is wrong and also somehow dangerous, as the non-linearity of the sigmoid is key to the solution of several problems. Also, sigmoid(0) = 0.5, and there is no x for which sigmoid(x) = 0. – Lordsandladies

Yeah, but it is 0.5 for any input of 0 without a bias, regardless of what the linear function before looks like. And that’s the point. You don’t normally train your sigmoid function, you just live with it. The linearity problem happens well before the sigmoid function. – Lisle

I get your point: the layer is not able to learn a different output for 0 than the one it started out with. That's correct and important. However, the "linear function argument" just does not apply in my opinion. Even with a bias, the function is still linear. The linearity property is misleading here. (Yes, I might be nitpicking.) – Lordsandladies

I’d say, that with a bias it’s affine. ( en.wikipedia.org/wiki/Affine_transformation#Representation ) – Lisle

Yes, you're correct. Thanks for pointing out that difference to me. (Why do we call it linear regression then, btw, although it's affine?) – Lordsandladies

The regression model itself is linear. It just operates on the augmented input space, where every vector has an element ‘1’ added as the last component. This would probably be different if the bias was fixed, but I’m not sure about that. People might still call it linear even then. – Lisle

Answer 7

When you use ANNs, you rarely know about the internals of the systems you want to learn. Some things cannot be learned without a bias. E.g., have a look at the following data: (0, 1), (1, 1), (2, 1), basically a function that maps any x to 1.

If you have a one layered network (or a linear mapping), you cannot find a solution. However, if you have a bias it's trivial!

In an ideal setting, a bias could also map all points to the mean of the target points and let the hidden neurons model the differences from that point.

Lordsandladies

Answer 8

Modification of neuron WEIGHTS alone only serves to manipulate the shape/curvature of your transfer function, and not its equilibrium/zero crossing point.

The introduction of bias neurons allows you to shift the transfer function curve horizontally (left/right) along the input axis while leaving the shape/curvature unaltered. This will allow the network to produce arbitrary outputs different from the defaults and hence you can customize/shift the input-to-output mapping to suit your particular needs.

See here for graphical explanation: http://www.heatonresearch.com/wiki/Bias

Working

The link is dead. – Molotov

Answer 9

If you're working with images, you might actually prefer to not use a bias at all. In theory, that way your network will be more independent of data magnitude, as in whether the picture is dark, or bright and vivid. And the net is going to learn to do it's job through studying relativity inside your data. Lots of modern neural networks utilize this.

For other data having biases might be critical. It depends on what type of data you're dealing with. If your information is magnitude-invariant --- if inputting [1,0,0.1] should lead to the same result as if inputting [100,0,10], you might be better off without a bias.

Phlegm

you're probably better off with normalization. What's an example of a modern network that uses "lack of bias" to produce magnitude invariaance? – Cushitic

@Cushitic , I believe, the usual ResNet utilizes that, as it's a part of it's "initialization", but I'm not exactly sure they did this for strictly this purpose, or, maybe for considerations of model size/efficiency and I'm not sure this concept is published anywhere. But I think it's completely understandable on a theory level. If you don't have a bias that doesn't scale, when you scale values, all of the outputs simply scale accordingly. Aware of this concept, or not, large part of modern architectures don't have biases at least in a large part of their structures. – Lynea

Take this with a grain of salt, though, as I don't currently remember if back when I tested this, if I had accounted for batchNorm introducing it's own bias that throws out the need for bias. It's kind of a nice idea in theory, but, please, don't trust it blindly, test. – Lynea

This is correct. Batch normalization, which is commonly used in modern architectures subsumes bias. See section 3.1 arxiv.org/pdf/1502.03167.pdf – Souther

Answer 10

In a couple of experiments in my masters thesis (e.g. page 59), I found that the bias might be important for the first layer(s), but especially at the fully connected layers at the end it seems not to play a big role.

This might be highly dependent on the network architecture / dataset.

Microgroove

That sounds completely analogous to the process of modeling systems "by hand" with linear regression. The simplest model would be Y_bar=mean(Y). Then you add complexity by including various X terms, stopping when there is no significant information gain. – Oshea

Answer 11

Bias determines how much angle your weight will rotate.

In a two-dimensional chart, weight and bias can help us to find the decision boundary of outputs.

Say we need to build a AND function, the input(p)-output(t) pair should be

{p=[0,0], t=0},{p=[1,0], t=0},{p=[0,1], t=0},{p=[1,1], t=1}

Now we need to find a decision boundary, and the ideal boundary should be:

See? W is perpendicular to our boundary. Thus, we say W decided the direction of boundary.

However, it is hard to find correct W at first time. Mostly, we choose original W value randomly. Thus, the first boundary may be this:

Now the boundary is parallel to the y axis.

We want to rotate the boundary. How?

By changing the W.

So, we use the learning rule function: W'=W+P:

W'=W+P is equivalent to W' = W + bP, while b=1.

Therefore, by changing the value of b(bias), you can decide the angle between W' and W. That is "the learning rule of ANN".

You could also read Neural Network Design by Martin T. Hagan / Howard B. Demuth / Mark H. Beale, chapter 4 "Perceptron Learning Rule"

Sequacious

Answer 12

To think in a simple way, if you have y=w1*x where y is your output and w1 is the weight, imagine a condition where x=0 then y=w1*x equals to 0.

If you want to update your weight you have to compute how much change by delw=target-y where target is your target output. In this case 'delw' will not change since y is computed as 0. So, suppose if you can add some extra value it will help y = w1x + w01, where bias=1 and weight can be adjusted to get a correct bias. Consider the example below.

In terms of line slope, intercept is a specific form of linear equations.

y = mx + b

Check the image

image

Here b is (0,2)

If you want to increase it to (0,3) how will you do it by changing the value of b the bias.

Proscribe

Answer 13

In simpler terms, biases allow for more and more variations of weights to be learnt/stored... (side-note: sometimes given some threshold). Anyway, more variations mean that biases add richer representation of the input space to the model's learnt/stored weights. (Where better weights can enhance the neural net’s guessing power)

For example, in learning models, the hypothesis/guess is desirably bounded by y=0 or y=1 given some input, in maybe some classification task... i.e some y=0 for some x=(1,1) and some y=1 for some x=(0,1). (The condition on the hypothesis/outcome is the threshold I talked about above. Note that my examples setup inputs X to be each x=a double or 2 valued-vector, instead of Nate's single valued x inputs of some collection X).

If we ignore the bias, many inputs may end up being represented by a lot of the same weights (i.e. the learnt weights mostly occur close to the origin (0,0). The model would then be limited to poorer quantities of good weights, instead of the many many more good weights it could better learn with bias. (Where poorly learnt weights lead to poorer guesses or a decrease in the neural net’s guessing power)

So, it is optimal that the model learns both close to the origin, but also, in as many places as possible inside the threshold/decision boundary. With the bias we can enable degrees of freedom close to the origin, but not limited to origin's immediate region.

Fluviatile

Answer 14

Expanding on zfy's explanation:

The equation for one input, one neuron, one output should look:

y = a * x + b * 1    and out = f(y)

where x is the value from the input node and 1 is the value of the bias node; y can be directly your output or be passed into a function, often a sigmoid function. Also note that the bias could be any constant, but to make everything simpler we always pick 1 (and probably that's so common that zfy did it without showing & explaining it).

Your network is trying to learn coefficients a and b to adapt to your data. So you can see why adding the element b * 1 allows it to fit better to more data: now you can change both slope and intercept.

If you have more than one input your equation will look like:

y = a0 * x0 + a1 * x1 + ... + aN * 1

Note that the equation still describes a one neuron, one output network; if you have more neurons you just add one dimension to the coefficient matrix, to multiplex the inputs to all nodes and sum back each node contribution.

That you can write in vectorized format as

A = [a0, a1, .., aN] , X = [x0, x1, ..., 1]
Y = A . XT

i.e. putting coefficients in one array and (inputs + bias) in another you have your desired solution as the dot product of the two vectors (you need to transpose X for the shape to be correct, I wrote XT a 'X transposed')

So in the end you can also see your bias as is just one more input to represent the part of the output that is actually independent of your input.

Tonkin

I seem to remember from Andrew Ng's class that the bias was left out in part of the training process. could you update your answer to explain that considering your conclusion that it's "just another input"? – Cushitic

@Cushitic I do not remember that from Andrew Ng's class, but that was a few years ago. Also Bias can be on or off depending what you are trying to learn. I read that in image processing they do not use it to allow scaling. To me if you use it, you use it also in training. The effect is to stabilize coefficients when all or part of the inputs is null or almost null. Why would you not use bias during training and then use it when using the NN to predict outputs for new inputs? How could that be useful? – Tonkin

No, it was more like, use it in the forward pass, but don't use it when calculating the gradient for backprop, or something like that. – Cushitic

@Cushitic I suppose that is a way to save some memory and time. You can decide you do not care to learn coefficients for the bias units. That can be fine if you have at least one hidden layer as the bias will provide some input to that layer and the output can be learned by the coefficients from the first to the second layer. I am not sure if the convergence speed will change. In my one layer example you are forced to learn also the bias coefficient as it is applied to the output. – Tonkin

In many simple problems, the target data has been demeaned and scaled, so no bias is needed.and the potential for excessive outlier influence in variables with large ranges is reduced. – Oshea

Answer 15

For all the ML books I studied, the W is always defined as the connectivity index between two neurons, which means the higher connectivity between two neurons.

The stronger the signals will be transmitted from the firing neuron to the target neuron or Y = w * X as a result to maintain the biological character of neurons, we need to keep the 1 >=W >= -1, but in the real regression, the W will end up with |W| >=1 which contradicts how the neurons are working.

As a result, I propose W = cos(theta), while 1 >= |cos(theta)|, and Y= a * X = W * X + b while a = b + W = b + cos(theta), b is an integer.

Theodolite

You could've formulated your answer in a more visually appealing manner. – Stillman

Answer 16

Bias acts as our anchor. It's a way for us to have some kind of baseline where we don't go below that. In terms of a graph, think of like y=mx+b it's like a y-intercept of this function.

output = input times the weight value and added a bias value and then apply an activation function.

Ladyinwaiting

Answer 17

The term bias is used to adjust the final output matrix as the y-intercept does. For instance, in the classic equation, y = mx + c, if c = 0, then the line will always pass through 0. Adding the bias term provides more flexibility and better generalisation to our neural network model.

Woodbine

Answer 18

The bias helps to get a better equation.

Imagine the input and output like a function y = ax + b and you need to put the right line between the input(x) and output(y) to minimise the global error between each point and the line, if you keep the equation like this y = ax, you will have one parameter for adaptation only, even if you find the best a minimising the global error it will be kind of far from the wanted value.

You can say the bias makes the equation more flexible to adapt to the best values

Curule