What's the fastest way of checking if a point is inside a polygon in python

Question

I found two main methods to look if a point belongs inside a polygon. One is using the ray tracing method used here, which is the most recommended answer, the other is using matplotlib path.contains_points (which seems a bit obscure to me). I will have to check lots of points continuously. Does anybody know if any of these two is more recommendable than the other or if there are even better third options?

UPDATE:

I checked the two methods and matplotlib looks much faster.

from time import time
import numpy as np
import matplotlib.path as mpltPath

# regular polygon for testing
lenpoly = 100
polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in np.linspace(0,2*np.pi,lenpoly)[:-1]]

# random points set of points to test 
N = 10000
points = np.random.rand(N,2)


# Ray tracing
def ray_tracing_method(x,y,poly):

    n = len(poly)
    inside = False

    p1x,p1y = poly[0]
    for i in range(n+1):
        p2x,p2y = poly[i % n]
        if y > min(p1y,p2y):
            if y <= max(p1y,p2y):
                if x <= max(p1x,p2x):
                    if p1y != p2y:
                        xints = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                    if p1x == p2x or x <= xints:
                        inside = not inside
        p1x,p1y = p2x,p2y

    return inside

start_time = time()
inside1 = [ray_tracing_method(point[0], point[1], polygon) for point in points]
print("Ray Tracing Elapsed time: " + str(time()-start_time))

# Matplotlib mplPath
start_time = time()
path = mpltPath.Path(polygon)
inside2 = path.contains_points(points)
print("Matplotlib contains_points Elapsed time: " + str(time()-start_time))

which gives,

Ray Tracing Elapsed time: 0.441395998001
Matplotlib contains_points Elapsed time: 0.00994491577148

Same relative difference was obtained one using a triangle instead of the 100 sides polygon. I will also check shapely since it looks a package just devoted to these kind of problems

Dieselelectric

Since matplotlib's implementation is C++ you can probably expect it to be faster. Considering that matplotlib is very widely used and since this is a very fundamental function - it's probably also safe to assume it's working correctly (even though it may seem "obscure"). Last but not least: Why not simply test it? – Olivarez

I updated the question with the test, as you predicted, matplotlib is much faster. I was concerned because matplotlib is not the most famous response in the different places I have looked, and I wanted to know if I was overlooking something (or some better package). Also matplotlib looked to be a big guy for a such a simple question. – Dieselelectric

This algorithm is wrong. It's not working for this case: polygon = np.array([[0, 0],[1, 0],[ 0, 1],[ 1, 1]]) points = np.array([[0.5, 0.5]]) Only matplotlib.path returns the correct result. – Vachon

Answer 1

You can consider shapely:

from shapely.geometry import Point
from shapely.geometry.polygon import Polygon

point = Point(0.5, 0.5)
polygon = Polygon([(0, 0), (0, 1), (1, 1), (1, 0)])
print(polygon.contains(point))

From the methods you've mentioned I've only used the second, path.contains_points, and it works fine. In any case depending on the precision you need for your test I would suggest creating a numpy bool grid with all nodes inside the polygon to be True (False if not). If you are going to make a test for a lot of points this might be faster (although notice this relies you are making a test within a "pixel" tolerance):

from matplotlib import path
import matplotlib.pyplot as plt
import numpy as np

first = -3
size  = (3-first)/100
xv,yv = np.meshgrid(np.linspace(-3,3,100),np.linspace(-3,3,100))
p = path.Path([(0,0), (0, 1), (1, 1), (1, 0)])  # square with legs length 1 and bottom left corner at the origin
flags = p.contains_points(np.hstack((xv.flatten()[:,np.newaxis],yv.flatten()[:,np.newaxis])))
grid = np.zeros((101,101),dtype='bool')
grid[((xv.flatten()-first)/size).astype('int'),((yv.flatten()-first)/size).astype('int')] = flags

xi,yi = np.random.randint(-300,300,100)/100,np.random.randint(-300,300,100)/100
vflag = grid[((xi-first)/size).astype('int'),((yi-first)/size).astype('int')]
plt.imshow(grid.T,origin='lower',interpolation='nearest',cmap='binary')
plt.scatter(((xi-first)/size).astype('int'),((yi-first)/size).astype('int'),c=vflag,cmap='Greens',s=90)
plt.show()

, the results is this:

Smoothbore

do you know which algorithm they use to detect the points in polygon ? – Zoon

Answer 2

If speed is what you need and extra dependencies are not a problem, you maybe find numba quite useful (now it is pretty easy to install, on any platform). The classic ray_tracing approach you proposed can be easily ported to numba by using numba @jit decorator and casting the polygon to a numpy array. The code should look like:

@jit(nopython=True)
def ray_tracing(x,y,poly):
    n = len(poly)
    inside = False
    p2x = 0.0
    p2y = 0.0
    xints = 0.0
    p1x,p1y = poly[0]
    for i in range(n+1):
        p2x,p2y = poly[i % n]
        if y > min(p1y,p2y):
            if y <= max(p1y,p2y):
                if x <= max(p1x,p2x):
                    if p1y != p2y:
                        xints = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                    if p1x == p2x or x <= xints:
                        inside = not inside
        p1x,p1y = p2x,p2y

    return inside

The first execution will take a little longer than any subsequent call:

%%time
polygon=np.array(polygon)
inside1 = [numba_ray_tracing_method(point[0], point[1], polygon) for 
point in points]

CPU times: user 129 ms, sys: 4.08 ms, total: 133 ms
Wall time: 132 ms

Which, after compilation will decrease to:

CPU times: user 18.7 ms, sys: 320 µs, total: 19.1 ms
Wall time: 18.4 ms

If you need speed at the first call of the function you can then pre-compile the code in a module using pycc. Store the function in a src.py like:

from numba import jit
from numba.pycc import CC
cc = CC('nbspatial')


@cc.export('ray_tracing',  'b1(f8, f8, f8[:,:])')
@jit(nopython=True)
def ray_tracing(x,y,poly):
    n = len(poly)
    inside = False
    p2x = 0.0
    p2y = 0.0
    xints = 0.0
    p1x,p1y = poly[0]
    for i in range(n+1):
        p2x,p2y = poly[i % n]
        if y > min(p1y,p2y):
            if y <= max(p1y,p2y):
                if x <= max(p1x,p2x):
                    if p1y != p2y:
                        xints = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                    if p1x == p2x or x <= xints:
                        inside = not inside
        p1x,p1y = p2x,p2y

    return inside


if __name__ == "__main__":
    cc.compile()

Build it with python src.py and run:

import nbspatial

import numpy as np
lenpoly = 100
polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in 
np.linspace(0,2*np.pi,lenpoly)[:-1]]

# random points set of points to test 
N = 10000
# making a list instead of a generator to help debug
points = zip(np.random.random(N),np.random.random(N))

polygon = np.array(polygon)

%%time
result = [nbspatial.ray_tracing(point[0], point[1], polygon) for point in points]

CPU times: user 20.7 ms, sys: 64 µs, total: 20.8 ms
Wall time: 19.9 ms

In the numba code I used: 'b1(f8, f8, f8[:,:])'

In order to compile with nopython=True, each var needs to be declared before the for loop.

In the prebuild src code the line:

@cc.export('ray_tracing' , 'b1(f8, f8, f8[:,:])')

Is used to declare the function name and its I/O var types, a boolean output b1 and two floats f8 and a two-dimensional array of floats f8[:,:] as input.

Edit Jan/4/2021

For my use case, I need to check if multiple points are inside a single polygon - In such a context, it is useful to take advantage of numba parallel capabilities to loop over a series of points. The example above can be changed to:

from numba import jit, njit
import numba
import numpy as np 

@jit(nopython=True)
def pointinpolygon(x,y,poly):
    n = len(poly)
    inside = False
    p2x = 0.0
    p2y = 0.0
    xints = 0.0
    p1x,p1y = poly[0]
    for i in numba.prange(n+1):
        p2x,p2y = poly[i % n]
        if y > min(p1y,p2y):
            if y <= max(p1y,p2y):
                if x <= max(p1x,p2x):
                    if p1y != p2y:
                        xints = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                    if p1x == p2x or x <= xints:
                        inside = not inside
        p1x,p1y = p2x,p2y

    return inside


@njit(parallel=True)
def parallelpointinpolygon(points, polygon):
    D = np.empty(len(points), dtype=numba.boolean) 
    for i in numba.prange(0, len(D)):
        D[i] = pointinpolygon(points[i,0], points[i,1], polygon)
    return D    

Note: pre-compiling the above code will not enable the parallel capabilities of numba (parallel CPU target is not supported by pycc/AOT compilation) see: https://github.com/numba/numba/issues/3336

Test:

import numpy as np
lenpoly = 100
polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in np.linspace(0,2*np.pi,lenpoly)[:-1]]
polygon = np.array(polygon)
N = 10000
points = np.random.uniform(-1.5, 1.5, size=(N, 2))

For N=10000 on a 72 core machine, returns:

%%timeit
parallelpointinpolygon(points, polygon)
# 480 µs ± 8.19 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Edit 17 Feb '21:

• fixing loop to start from 0 instead of 1 (thanks @mehdi):

for i in numba.prange(0, len(D))

Edit 20 Feb '21:

Follow-up on the comparison made by @mehdi, I am adding a GPU-based method below. It uses the point_in_polygon method, from the cuspatial library:

    import numpy as np
    import cudf
    import cuspatial

    N = 100000002
    lenpoly = 1000
    polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in 
    np.linspace(0,2*np.pi,lenpoly)]
    polygon = np.array(polygon)
    points = np.random.uniform(-1.5, 1.5, size=(N, 2))


    x_pnt = points[:,0]
    y_pnt = points[:,1]
    x_poly =polygon[:,0]
    y_poly = polygon[:,1]
    result = cuspatial.point_in_polygon(
        x_pnt,
        y_pnt,
        cudf.Series([0], index=['geom']),
        cudf.Series([0], name='r_pos', dtype='int32'), 
        x_poly, 
        y_poly,
    )

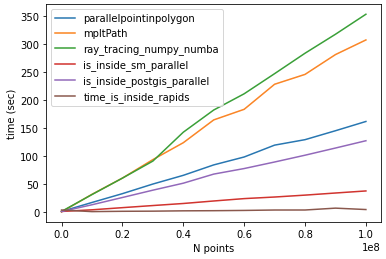
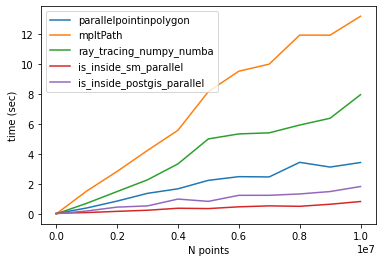
Following @Mehdi comparison. For N=100000002 and lenpoly=1000 - I got the following results:

 time_parallelpointinpolygon:         161.54760098457336 
 time_mpltPath:                       307.1664695739746 
 time_ray_tracing_numpy_numba:        353.07356882095337 
 time_is_inside_sm_parallel:          37.45389246940613 
 time_is_inside_postgis_parallel:     127.13793849945068 
 time_is_inside_rapids:               4.246025562286377

hardware specs:

• CPU Intel xeon E1240
• GPU Nvidia GTX 1070

Notes:

• The cuspatial.point_in_poligon method, is quite robust and powerful, it offers the ability to work with multiple and complex polygons (I guess at the expense of performance)

• The numba methods can also be 'ported' on the GPU - it will be interesting to see a comparison which includes a porting to cuda of fastest method mentioned by @Mehdi (is_inside_sm).

Antimonic

@epifanio, good implementation, but your code does not always return correct answers. The results of the original ray_tracing_method() from post#1 and matplotlib.path are always matching. – Vachon

@Mehdi, thanks for the comment - the code in the answer is supposed to replicate the code in the question (ray_tracing_method() from post#1) - do you a snipped of code to reproduce a mismatch between the two approaches that I can use to debug the problem? – Antimonic

@epifanio, the difference is the first point. use np.random.seed(2). The rest is your code. here is the code: path = mpltPath.Path(polygon) inside1 = path.contains_points(points) inside2=parallelpointinpolygon(points, polygon) print('number of diffs:',len(inside1) - sum(inside2==inside1)) – Vachon

@epifanio, I found the issue! You missed the 1sr point in parallelpointinpolygon: for i in numba.prange(1, len(D)): . It must start from zero. for i in numba.prange(0, len(D)): – Vachon

Hi, what is the is_inside_rapids? we see it in the graph but not in text/code. Ty for the comparisons. – Lombroso

is_inside_rapid is a wrapper around the method: cuspatial.point_in_polygon the code is in the 'edit 20 Feb 21' – Antimonic

How does the shapely package compare to the other solutions? – Conceptualism

Answer 3

Comparison of different methods

I found other methods to check if a point is inside a polygon (here). I tested two of them only (is_inside_sm and is_inside_postgis) and the results were the same as the other methods.

Thanks to @epifanio, I parallelized the codes and compared them with @epifanio and @user3274748 (ray_tracing_numpy) methods. Note that both methods had a bug so I fixed them as shown in their codes below.

One more thing that I found is that the code provided for creating a polygon does not generate a closed path np.linspace(0,2*np.pi,lenpoly)[:-1]. As a result, the codes provided in above GitHub repository may not work properly. So It's better to create a closed path (first and last points should be the same).

Codes

Method 1: parallelpointinpolygon

from numba import jit, njit
import numba
import numpy as np 

@jit(nopython=True)
def pointinpolygon(x,y,poly):
    n = len(poly)
    inside = False
    p2x = 0.0
    p2y = 0.0
    xints = 0.0
    p1x,p1y = poly[0]
    for i in numba.prange(n+1):
        p2x,p2y = poly[i % n]
        if y > min(p1y,p2y):
            if y <= max(p1y,p2y):
                if x <= max(p1x,p2x):
                    if p1y != p2y:
                        xints = (y-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
                    if p1x == p2x or x <= xints:
                        inside = not inside
        p1x,p1y = p2x,p2y

    return inside


@njit(parallel=True)
def parallelpointinpolygon(points, polygon):
    D = np.empty(len(points), dtype=numba.boolean) 
    for i in numba.prange(0, len(D)):   #<-- Fixed here, must start from zero
        D[i] = pointinpolygon(points[i,0], points[i,1], polygon)
    return D  

---

Method 2: ray_tracing_numpy_numba

@jit(nopython=True)
def ray_tracing_numpy_numba(points,poly):
    x,y = points[:,0], points[:,1]
    n = len(poly)
    inside = np.zeros(len(x),np.bool_)
    p2x = 0.0
    p2y = 0.0
    p1x,p1y = poly[0]
    for i in range(n+1):
        p2x,p2y = poly[i % n]
        idx = np.nonzero((y > min(p1y,p2y)) & (y <= max(p1y,p2y)) & (x <= max(p1x,p2x)))[0]
        if len(idx):    # <-- Fixed here. If idx is null skip comparisons below.
            if p1y != p2y:
                xints = (y[idx]-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
            if p1x == p2x:
                inside[idx] = ~inside[idx]
            else:
                idxx = idx[x[idx] <= xints]
                inside[idxx] = ~inside[idxx]    

        p1x,p1y = p2x,p2y
    return inside 

Method 3: Matplotlib contains_points

path = mpltPath.Path(polygon,closed=True)  # <-- Very important to mention that the path 
                                           #     is closed (default is false)

Method 4: is_inside_sm (got it from here)

@jit(nopython=True)
def is_inside_sm(polygon, point):
    length = len(polygon)-1
    dy2 = point[1] - polygon[0][1]
    intersections = 0
    ii = 0
    jj = 1

    while ii<length:
        dy  = dy2
        dy2 = point[1] - polygon[jj][1]

        # consider only lines which are not completely above/bellow/right from the point
        if dy*dy2 <= 0.0 and (point[0] >= polygon[ii][0] or point[0] >= polygon[jj][0]):

            # non-horizontal line
            if dy<0 or dy2<0:
                F = dy*(polygon[jj][0] - polygon[ii][0])/(dy-dy2) + polygon[ii][0]

                if point[0] > F: # if line is left from the point - the ray moving towards left, will intersect it
                    intersections += 1
                elif point[0] == F: # point on line
                    return 2

            # point on upper peak (dy2=dx2=0) or horizontal line (dy=dy2=0 and dx*dx2<=0)
            elif dy2==0 and (point[0]==polygon[jj][0] or (dy==0 and (point[0]-polygon[ii][0])*(point[0]-polygon[jj][0])<=0)):
                return 2

        ii = jj
        jj += 1

    #print 'intersections =', intersections
    return intersections & 1  


@njit(parallel=True)
def is_inside_sm_parallel(points, polygon):
    ln = len(points)
    D = np.empty(ln, dtype=numba.boolean) 
    for i in numba.prange(ln):
        D[i] = is_inside_sm(polygon,points[i])
    return D  

Method 5: is_inside_postgis (got it from here)

@jit(nopython=True)
def is_inside_postgis(polygon, point):
    length = len(polygon)
    intersections = 0

    dx2 = point[0] - polygon[0][0]
    dy2 = point[1] - polygon[0][1]
    ii = 0
    jj = 1

    while jj<length:
        dx  = dx2
        dy  = dy2
        dx2 = point[0] - polygon[jj][0]
        dy2 = point[1] - polygon[jj][1]

        F =(dx-dx2)*dy - dx*(dy-dy2);
        if 0.0==F and dx*dx2<=0 and dy*dy2<=0:
            return 2;

        if (dy>=0 and dy2<0) or (dy2>=0 and dy<0):
            if F > 0:
                intersections += 1
            elif F < 0:
                intersections -= 1

        ii = jj
        jj += 1

    #print 'intersections =', intersections
    return intersections != 0  


@njit(parallel=True)
def is_inside_postgis_parallel(points, polygon):
    ln = len(points)
    D = np.empty(ln, dtype=numba.boolean) 
    for i in numba.prange(ln):
        D[i] = is_inside_postgis(polygon,points[i])
    return D  

Benchmark

Timing for 10 million points:

parallelpointinpolygon Elapsed time:      4.0122294425964355
Matplotlib contains_points Elapsed time: 14.117807388305664
ray_tracing_numpy_numba Elapsed time:     7.908452272415161
sm_parallel Elapsed time:                 0.7710440158843994
is_inside_postgis_parallel Elapsed time:  2.131121873855591

Here is the code.

import matplotlib.pyplot as plt
import matplotlib.path as mpltPath
from time import time
import numpy as np

np.random.seed(2)

time_parallelpointinpolygon=[]
time_mpltPath=[]
time_ray_tracing_numpy_numba=[]
time_is_inside_sm_parallel=[]
time_is_inside_postgis_parallel=[]
n_points=[]

for i in range(1, 10000002, 1000000): 
    n_points.append(i)
    
    lenpoly = 100
    polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in np.linspace(0,2*np.pi,lenpoly)]
    polygon = np.array(polygon)
    N = i
    points = np.random.uniform(-1.5, 1.5, size=(N, 2))
    
    
    #Method 1
    start_time = time()
    inside1=parallelpointinpolygon(points, polygon)
    time_parallelpointinpolygon.append(time()-start_time)

    # Method 2
    start_time = time()
    path = mpltPath.Path(polygon,closed=True)
    inside2 = path.contains_points(points)
    time_mpltPath.append(time()-start_time)

    # Method 3
    start_time = time()
    inside3=ray_tracing_numpy_numba(points,polygon)
    time_ray_tracing_numpy_numba.append(time()-start_time)

    # Method 4
    start_time = time()
    inside4=is_inside_sm_parallel(points,polygon)
    time_is_inside_sm_parallel.append(time()-start_time)

    # Method 5
    start_time = time()
    inside5=is_inside_postgis_parallel(points,polygon)
    time_is_inside_postgis_parallel.append(time()-start_time)


    
plt.plot(n_points,time_parallelpointinpolygon,label='parallelpointinpolygon')
plt.plot(n_points,time_mpltPath,label='mpltPath')
plt.plot(n_points,time_ray_tracing_numpy_numba,label='ray_tracing_numpy_numba')
plt.plot(n_points,time_is_inside_sm_parallel,label='is_inside_sm_parallel')
plt.plot(n_points,time_is_inside_postgis_parallel,label='is_inside_postgis_parallel')
plt.xlabel("N points")
plt.ylabel("time (sec)")
plt.legend(loc = 'best')
plt.show()

CONCLUSION

The fastest algorithms are:

1- is_inside_sm_parallel

2- is_inside_postgis_parallel

3- parallelpointinpolygon (@epifanio)

Vachon

Great job @Mehdi, will you be interested in testing a GPU version as well? I'd like if there is any speed up in applying the point_in_polygon methods on a set of points stored in a cudf datfarme. I also noticed that cuspatial from rapidsai has a point in polygon method which I didn't test yet. – Antimonic

I would like to test it, but I don't have access to cuda gpu at the moment. – Vachon

A free instance of google-colab has GPU support - if of interest we can share a notebook to perform the comparison there. – Antimonic

Looks interesting. – Vachon

I added the point_in_polygon method from the cuspatial library. (100000000 points) - I will add the relative code and pics to the answer. What is left is to try the numba-cuda methods. – Antimonic

No idea how to use them. I got errors TypingError: Invalid use of Function(<built-in function getitem>) with argument(s) of type(s): (reflected list(reflected list(int64)), (slice<a:b>, Literal[int](0))). Seems like list not supported and shapely.polygons also. – Fissile

Answer 4

Your test is good, but it measures only some specific situation: we have one polygon with many vertices, and long array of points to check them within polygon.

Moreover, I suppose that you're measuring not matplotlib-inside-polygon-method vs ray-method, but matplotlib-somehow-optimized-iteration vs simple-list-iteration

Let's make N independent comparisons (N pairs of point and polygon)?

# ... your code...
lenpoly = 100
polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in np.linspace(0,2*np.pi,lenpoly)[:-1]]

M = 10000
start_time = time()
# Ray tracing
for i in range(M):
    x,y = np.random.random(), np.random.random()
    inside1 = ray_tracing_method(x,y, polygon)
print "Ray Tracing Elapsed time: " + str(time()-start_time)

# Matplotlib mplPath
start_time = time()
for i in range(M):
    x,y = np.random.random(), np.random.random()
    inside2 = path.contains_points([[x,y]])
print "Matplotlib contains_points Elapsed time: " + str(time()-start_time)

Result:

Ray Tracing Elapsed time: 0.548588991165
Matplotlib contains_points Elapsed time: 0.103765010834

Matplotlib is still much better, but not 100 times better. Now let's try much simpler polygon...

lenpoly = 5
# ... same code

result:

Ray Tracing Elapsed time: 0.0727779865265
Matplotlib contains_points Elapsed time: 0.105288982391

Geaghan

Answer 5

I will just leave it here, just rewrote the code above using numpy, maybe somebody finds it useful:

def ray_tracing_numpy(x,y,poly):
    n = len(poly)
    inside = np.zeros(len(x),np.bool_)
    p2x = 0.0
    p2y = 0.0
    xints = 0.0
    p1x,p1y = poly[0]
    for i in range(n+1):
        p2x,p2y = poly[i % n]
        idx = np.nonzero((y > min(p1y,p2y)) & (y <= max(p1y,p2y)) & (x <= max(p1x,p2x)))[0]
        if p1y != p2y:
            xints = (y[idx]-p1y)*(p2x-p1x)/(p2y-p1y)+p1x
        if p1x == p2x:
            inside[idx] = ~inside[idx]
        else:
            idxx = idx[x[idx] <= xints]
            inside[idxx] = ~inside[idxx]    

        p1x,p1y = p2x,p2y
    return inside    

Wrapped ray_tracing into

def ray_tracing_mult(x,y,poly):
    return [ray_tracing(xi, yi, poly[:-1,:]) for xi,yi in zip(x,y)]

Tested on 100000 points, results:

ray_tracing_mult 0:00:00.850656
ray_tracing_numpy 0:00:00.003769

Erichericha

how can i return only true or false for one poly and one x,y ? – Diaconicum

I would use @Antimonic solution if you are only doing one poly. The NumPy solution is better for computation in larger batches. – Turro

Would be great if working example was provided. Don't want spend 20 minutes trying to figure out what shapes you are expecting. – Inhere

Answer 6

pure numpy vectorized implementation of the Even-odd rule

The other answers are either a slow python loop or requires external dependancies or cython treatment.

import numpy as np
        
def points_in_polygon(polygon, pts):
    pts = np.asarray(pts,dtype='float32')
    polygon = np.asarray(polygon,dtype='float32')
    contour2 = np.vstack((polygon[1:], polygon[:1]))
    test_diff = contour2-polygon
    mask1 = (pts[:,None] == polygon).all(-1).any(-1)
    m1 = (polygon[:,1] > pts[:,None,1]) != (contour2[:,1] > pts[:,None,1])
    slope = ((pts[:,None,0]-polygon[:,0])*test_diff[:,1])-(test_diff[:,0]*(pts[:,None,1]-polygon[:,1]))
    m2 = slope == 0
    mask2 = (m1 & m2).any(-1)
    m3 = (slope < 0) != (contour2[:,1] < polygon[:,1])
    m4 = m1 & m3
    count = np.count_nonzero(m4,axis=-1)
    mask3 = ~(count%2==0)
    mask = mask1 | mask2 | mask3
    return mask

    
N = 1000000
lenpoly = 1000
polygon = [[np.sin(x)+0.5,np.cos(x)+0.5] for x in np.linspace(0,2*np.pi,lenpoly)]
polygon = np.array(polygon,dtype='float32')
points = np.random.uniform(-1.5, 1.5, size=(N, 2)).astype('float32')
mask = points_in_polygon(polygon, points)

1 mil points with polygon of size 1000 took 44s.

Its orders of magnitude slower than the other implementations but still faster than the python loop and only uses numpy.

Wiggly

@GeneralCode python opencv's implementation is fast for testing a single point (faster than my code even). but running 1 million points would take forever in a loop. I created this algo to batch calculate bc opencv in a loop was too slow for me to test 1000s of points – Wiggly

Answer 7

inpoly is the gold standard for doing in polygon checks in python, and can handle huge queries:

https://github.com/dengwirda/inpoly-python

simple usage:

from inpoly import inpoly2
import numpy as np
    
xmin, xmax, ymin, ymax = 0, 1, 0, 1
x0, y0, x1, y1 = 0.5, 0.5, 0, 1

#define any n-sided polygon
p = np.array([[xmin, ymin],
              [xmax, ymin],
              [xmax, ymax],
              [xmin, ymax],
              [xmin, ymin]])

#define some coords
coords = np.array([[x0, y0],
                   [x1, y1]])

#get boolean mask for points if in or on polygon perimeter
isin, ison = inpoly2(coords, p)

the C implementation in the backend is lightning fast

Rheta

This is far slower than matplotlibs point_in_path – Parkinson

@Parkinson I'm assuming you mean matplotlib.path's contains_points. It depends on the query size and size of the polygon. For example, 1000pts in a 4pt box, MPL twice as fast. 10M points in a 10K pt box, inpoly2 about 60x faster than MPL. As with most things, depends on the application. Inpoly2 is amazing for large queries. – Rheta

Answer 8

The Asymptotically fastest algorithm is the following.

    def build_edge_list(polygon):
        edge_list = []
        for i in range(0, len(polygon) - 1):
            if (polygon[i].imag, polygon[i].real) < (
                polygon[i + 1].imag,
                polygon[i + 1].real,
            ):
                edge_list.append((polygon[i], i))
                edge_list.append((polygon[i + 1], ~i))
            else:
                edge_list.append((polygon[i], ~i))
                edge_list.append((polygon[i + 1], i))
    
        def sort_key(e):
            return e[0].imag, e[0].real, ~e[1]
    
        edge_list.sort(key=sort_key)
        return edge_list
    
    
    def build_scanbeam(edge_list):
        actives = []
        actives_table = []
        events = []
        y = -float("inf")
        for pt, index in edge_list:
            if y != pt.imag:
                actives_table.append(list(actives))
                events.append(pt.imag)
            if index >= 0:
                actives.append(index)
            else:
                actives.remove(~index)
            y = pt.imag
        actives_table.append(list(actives))
        largest_actives = max([len(a) for a in actives_table])
        scan = np.zeros((len(actives_table), largest_actives), dtype=int)
        scan -= 1
        for i, active in enumerate(actives_table):
            scan[i, 0 : len(active)] = active
        return scan, events
    
    
    def points_in_polygon(polygon, point):
        edge_list = build_edge_list(polygon)
        scan, events = build_scanbeam(edge_list)
        pts_y = np.imag(point)
        idx = np.searchsorted(events, pts_y)
        actives = scan[idx]
        a = polygon[actives]
        b = polygon[actives + 1]
    
        a = np.where(actives == -1, np.nan + np.nan * 1j, a)
        b = np.where(actives == -1, np.nan + np.nan * 1j, b)
    
        old_np_seterr = np.seterr(invalid="ignore", divide="ignore")
        try:
            # If horizontal slope is undefined. But, all x-ints are at x since x0=x1
            m = (b.imag - a.imag) / (b.real - a.real)
            y0 = a.imag - (m * a.real)
            ys = np.reshape(np.repeat(np.imag(point), y0.shape[1]), y0.shape)
            x_intercepts = np.where(~np.isinf(m), (ys - y0) / m, a.real)
        finally:
            np.seterr(**old_np_seterr)
    
        xs = np.reshape(np.repeat(np.real(point), y0.shape[1]), y0.shape)
        results = np.sum(x_intercepts <= xs, axis=1)
        results %= 2
        return results

This is actually faster (in time complexity than inpoly). Though the C++ means that it doesn't actually go faster until it's in the trillions of polygons. (but, we're talking 1 order of magnitude rather not even close).

import time

import numpy as np

def points_in_polygon_Ta946(polygon, pts):
    pts = np.asarray(pts, dtype="float32")
    polygon = np.asarray(polygon, dtype="float32")
    contour2 = np.vstack((polygon[1:], polygon[:1]))
    test_diff = contour2 - polygon
    mask1 = (pts[:, None] == polygon).all(-1).any(-1)
    m1 = (polygon[:, 1] > pts[:, None, 1]) != (contour2[:, 1] > pts[:, None, 1])
    slope = ((pts[:, None, 0] - polygon[:, 0]) * test_diff[:, 1]) - (
            test_diff[:, 0] * (pts[:, None, 1] - polygon[:, 1])
    )
    m2 = slope == 0
    mask2 = (m1 & m2).any(-1)
    m3 = (slope < 0) != (contour2[:, 1] < polygon[:, 1])
    m4 = m1 & m3
    count = np.count_nonzero(m4, axis=-1)
    mask3 = ~(count % 2 == 0)
    mask = mask1 | mask2 | mask3
    return mask


def build_edge_list(polygon):
    edge_list = []
    for i in range(0, len(polygon) - 1):
        if (polygon[i].imag, polygon[i].real) < (
                polygon[i + 1].imag,
                polygon[i + 1].real,
        ):
            edge_list.append((polygon[i], i))
            edge_list.append((polygon[i + 1], ~i))
        else:
            edge_list.append((polygon[i], ~i))
            edge_list.append((polygon[i + 1], i))

    def sort_key(e):
        return e[0].imag, e[0].real, ~e[1]

    edge_list.sort(key=sort_key)
    return edge_list


def build_scanbeam(edge_list):
    actives = []
    actives_table = []
    events = []
    y = -float("inf")
    for pt, index in edge_list:
        if y != pt.imag:
            actives_table.append(list(actives))
            events.append(pt.imag)
        if index >= 0:
            actives.append(index)
        else:
            actives.remove(~index)
        y = pt.imag
    actives_table.append(list(actives))
    largest_actives = max([len(a) for a in actives_table])
    scan = np.zeros((len(actives_table), largest_actives), dtype=int)
    scan -= 1
    for i, active in enumerate(actives_table):
        scan[i, 0: len(active)] = active
    return scan, events


def points_in_polygon(polygon, point):
    edge_list = build_edge_list(polygon)
    scan, events = build_scanbeam(edge_list)
    pts_y = np.imag(point)
    idx = np.searchsorted(events, pts_y)
    actives = scan[idx]
    a = polygon[actives]
    b = polygon[actives + 1]

    a = np.where(actives == -1, np.nan + np.nan * 1j, a)
    b = np.where(actives == -1, np.nan + np.nan * 1j, b)

    old_np_seterr = np.seterr(invalid="ignore", divide="ignore")
    try:
        # If horizontal slope is undefined. But, all x-ints are at x since x0=x1
        m = (b.imag - a.imag) / (b.real - a.real)
        y0 = a.imag - (m * a.real)
        ys = np.reshape(np.repeat(np.imag(point), y0.shape[1]), y0.shape)
        x_intercepts = np.where(~np.isinf(m), (ys - y0) / m, a.real)
    finally:
        np.seterr(**old_np_seterr)

    xs = np.reshape(np.repeat(np.real(point), y0.shape[1]), y0.shape)
    results = np.sum(x_intercepts <= xs, axis=1)
    results %= 2
    return results


N = 50000
lenpoly = 1000
polygon = [
    [np.sin(x) + 0.5, np.cos(x) + 0.5]
    for x in np.linspace(0, 2 * np.pi, lenpoly)
]
polygon = np.array(polygon, dtype="float32")

points = np.random.uniform(-1.5, 1.5, size=(N, 2)).astype("float32")
t = time.time()
mask = points_in_polygon_Ta946(polygon, points)
t1 = time.time() - t

# Convert to correct format.
t = time.time()
points = points[:, 0] + points[:, 1] * 1j
pg = polygon[:, 0] + polygon[:, 1] * 1j
r = points_in_polygon(pg, points)
t2 = time.time() - t

for i in range(N):
    assert(bool(mask[i]) == bool(r[i]))

try:
    print(
        f"geomstr points in poly took {t2} seconds. Raytraced-numpy took {t1}. Speed-up {t1 / t2}x"
    )
except ZeroDivisionError:
    pass

Of answers here in pure python (with numpy) Ta946's answer is by far the best. But, as an answer it's still doing raytracing which is ultimately a much slower algorithm, O(N*logN). inpoly is using a O(log(N)*K) algorithm and this algorithm here is a O(log(N)*log(K)) algorithm. Though K is almost always a fraction of the size of N so it's not easy to beat the running it in C++ aspect of that solution.

geomstr points in poly took 0.03299069404602051 seconds. Raytraced-numpy took 3.781247615814209. Speed-up 114.61558251971121x

And that's at 50k points, the difference gets more pronounced with higher sample sizes.

Fenella

Answer 9

you can use Geopandas sjoin. probably the easiest

import geopandas as gpd
gpd.sjoin(points, polygon, op = 'within') 

Shedd