Covering an arbitrary area with circles of equal radius

Question

How would an algorithm work that covers an arbitrary area with circles of equal radius?

The radius of the circle and the size and shape of the area are arbitrarily given. The area should be covered with as few circles as possible. The circles may overlap.

Is there an algorithm that will handle this?

Counterfoil

Circles don't tesellate, so you can't do this perfectly without overlap. Can you clarify your problem? – Bindman

Edited my answer to include a method that covers the whole area. :-) – Tendon

How important is "covered with as few circles as possible"? If it isn't critical to use the absolute minimum number of circles, then techniques like Eric Bainville's can yield good results for many cases. – Telugu

Must the circles be the same size? May the circles overlap the edge of the shape? – Bindman

The circles have to be same size. They may overlap the edge of the shape. – Counterfoil

I think the hexagonal approach is a good approximation for solving the equal circle covering problem. However, it is sometimes the case that it does not perfectly solve the problem. You may want to check out: arxiv.org/abs/2003.04839 which uses genetic algorithms and BFGS optimization to solve this problem. The source code is contained in the paper as well. – Lubalubba

Answer 1

I know that question may be a bit outdated but recently I got a similar problem with covering geographic area with equal circles using hexagonal grid and this is how I solved it:

1. my input data were radius of circle given in meters and coordinates of borders of the area
2. first I found the bounds rectangle that covers given area
3. then starting from the left bottom I move the point by distance equaling double the height of the triangle used to build the hexagon (its side is the same of radius of my circle) and bearing of 0 degrees using Vincenty's formulae
4. for each point I found, I check if it intersects with my input area, if does I save it, other way I skip it
5. when I got to the edge I do one more check to ensure that I will get all points within the area
6. I move the point by bearing of 60 degrees, check it, then by 120 degrees, check again
7. go back to 3rd step but now I move the points by bearing of 180 degrees
8. and the edge again one more check and then like in step 6th but first 120 degrees then 60 degrees
9. continue until you got to the top edge of rectangle

like in given image, of course you can increase the accuracy by decreasing radius of circle

I know that this is not the best option but it works pretty well for me.

I hope it's quite understandable and will help anyone.

Nealah

Hi, I'm looking to solve the exact same problem though I'm not totally following your sudo code. Would you be able to provide me with your implementation? Thanks! – Workable

Answer 2

Hope I have understood your question right...

It can be proved that Hexagonal Close Packing (HCP) of spheres covers the maximum volume, using spheres. Therefore, I assume that doing HCP with circles will also cover the maximum area using circles. Tessellate your area with triangles and place a circle with the centre at each vertex of the triangle, with the radius half the length of the side of the triangle. See this for an image of the algorithm I am talking about.

Note: This is similar to the close packing of atoms in a unit cell.

EDIT: My previous method covers as much of the area as possible, without overlapping. If overlapping is allowed, then (I believe that) the following method would cover the whole area with minimum overlapping.

As you probably know, there are only 3 tessellations of 2D space with regular polygons - using squares, triangles or hexagons. The strategy is to tessellate using one of these polygons and then circumscribe a circle to every polygon. A hexagon would waste the minimum area using this method.

Therefore, from the radius of the given circle, calculate the size of the needed hexagons, tessellate the area using the hexagons and then circumscribe a circle onto each hexagon.

NB: Eric Bainville suggested a similar method.

-- Flaviu Cipcigan

Tendon

This technique does not work, because it doesn't cover the whole area. – Counterfoil

Answer 3

Without knowing more about your constraints, I would suggest taking a regular covering of the plane, with disks corresponding to the regular hexagons of an hexagonal tiling. Then keep all disks intersecting the shape.

Dorweiler

Answer 4

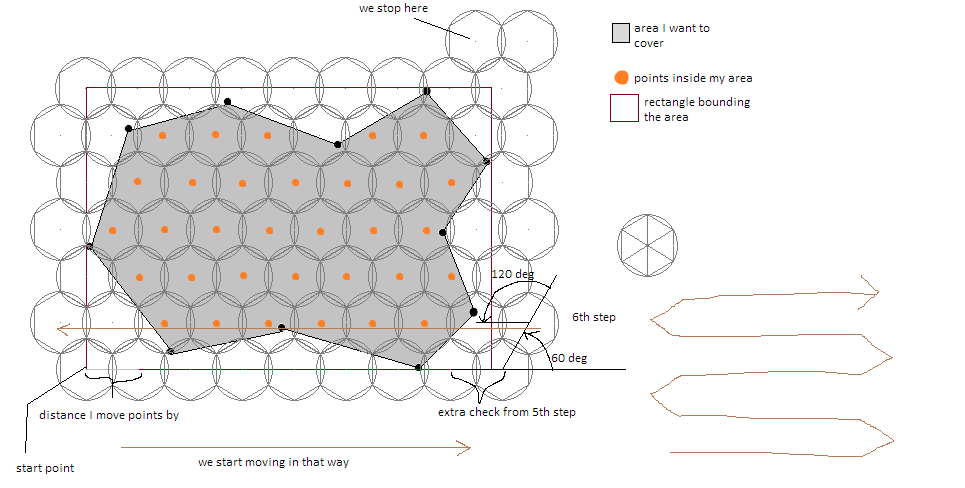
So far there's only one code snippet in the answer to this question and I couldn't get it work. I have a similar problem - I want to find every Ethiopian restaurant in the lower 48 of the USA. To do that I want to use the Google Places API "Nearby Search" feature and step across the lower 48, one 100km circle (the max search area for the API) at a time without missing any spots. I ended up using baskax's approach but instead of polygon's I used squares since they were just easier.

I wanted to make the code as polite as possible so that reviewers could more easily understand and improve or tweak it. Because of that, it's not terribly compact or fast.

from pyproj import Geod
import geopandas as gpd
from shapely.geometry import Point
from shapely.ops import nearest_points
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse, Rectangle
from math import sqrt
from decimal import Decimal
from types import SimpleNamespace


class RadarCoverage():
    def __init__(self, map_data_4326: gpd.GeoDataFrame, radar_radius_meters):
        # Setup our graph info so that we can visiualize the reesult
        self.fig, self.ax1 = plt.subplots(nrows=1, ncols=1, figsize=(12, 12))
        self.ax1.set_title("WGS84 Grid System")
        self.ax1.set_aspect(aspect=1)
        plt.tight_layout()

        # Map data
        self.geod = Geod(ellps="WGS84")
        self.map_data = map_data_4326
        self.map_data.plot(ax=self.ax1, facecolor="gray")
        self.ploygons_of_areas_of_interest = [i for i in self.map_data.geometry]

        # Bounding box, based on map data
        raw_bounds = self.map_data.bounds
        self.min_x = raw_bounds['minx'].min()
        self.min_y = raw_bounds['miny'].min()
        self.max_x = raw_bounds['maxx'].max()
        self.max_y = raw_bounds['maxy'].max()
        bounding_box_width = self.max_x-self.min_x
        bounding_box_height = self.max_y-self.min_y
        self.ax1.add_patch(plt.Rectangle((self.min_x, self.min_y), bounding_box_width, bounding_box_height, fill=False))

        # Base radar info
        self.radar_radius = Decimal(radar_radius_meters)
        half_of_square_side = sqrt((self.radar_radius**2)/2)
        self.square_side = 2*half_of_square_side
        self.initial_longitude_of_scan = self.min_x
        self.initial_latitude_of_scan = self.max_y

    def step(self, starting_long, starting_lat, direction, distance_meters):
        if direction == "up":
            azimuth = Decimal(0)
        if direction == "right":
            azimuth = Decimal(90)
        if direction == "down":
            azimuth = Decimal(180)
        if direction == "left":
            azimuth = Decimal(270)
        ending_long, ending_lat, back_azimuth = self.geod.fwd(lons=starting_long, lats=starting_lat, az=azimuth, dist=distance_meters)
        step_polite = {"long": ending_long, "lat": ending_lat, "long_delta": abs(ending_long-starting_long), "lat_delta": abs(ending_lat-starting_lat)}
        return SimpleNamespace(**step_polite)

    def scan(self):
        current_longitude = self.min_x
        current_latitude = self.max_y
        list_of_centers = []

        while current_latitude > self.min_y:
            while current_longitude < self.max_x:
                # Step down and over to define the area of the sqaure
                step_down_coord = self.step(current_longitude, current_latitude, "down", self.square_side)
                step_over_coord = self.step(step_down_coord.long, step_down_coord.lat, "right", self.square_side)

                # Create that square and find it's center
                square = Rectangle((step_down_coord.long, step_down_coord.lat), step_over_coord.long_delta, step_down_coord.lat_delta,  fill=False, color='red')
                square_center = square.get_center()
                shapely_square_center = Point(square_center)

                # Determine if the radar ping from the center of that square would cover an area of interet
                radar_touches_area_of_interest = False
                for poly in self.ploygons_of_areas_of_interest:
                    p1, p2 = nearest_points(poly, shapely_square_center)
                    azimuth1, azimuth2, distance = self.geod.inv(square_center[0], square_center[1], p1.x, p1.y)
                    if distance <= self.radar_radius:
                        radar_touches_area_of_interest = True

                # If it does, log the radar centerpoint, build the square tile, and build the radar coverage
                if radar_touches_area_of_interest:
                    list_of_centers.append(square_center)

                    plt.plot(square_center[0], square_center[1], 'r+')
                    self.ax1.add_patch(square)

                    # Note that the radar coverage will often be elliptical in shape due to projection distotion
                    # To account for this we build each arm of the ellipse idenpendently
                    top_step = self.step(square_center[0], square_center[1], "up", self.radar_radius)
                    bottom_step = self.step(square_center[0], square_center[1], "down", self.radar_radius)
                    right_step = self.step(square_center[0], square_center[1], "right", self.radar_radius)
                    left_step = self.step(square_center[0], square_center[1], "left", self.radar_radius)
                    ellipsis_width = right_step.long_delta + left_step.long_delta
                    ellipsis_height = top_step.lat_delta + bottom_step.lat_delta

                    radar_coverage = Ellipse(square_center, ellipsis_width, ellipsis_height, fill=False, color='red')
                    self.ax1.add_patch(radar_coverage)

                current_longitude = current_longitude + step_over_coord.long_delta

            current_latitude = current_latitude - step_down_coord.lat_delta
            current_longitude = self.initial_longitude_of_scan
        plt.show()
        return list_of_centers


if __name__ == "__main__":    
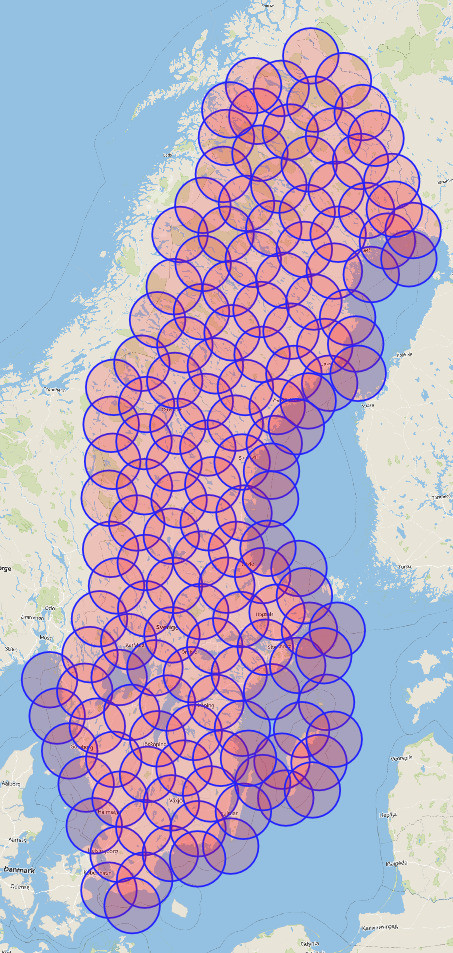
    world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
    sweden = world[world.name == "Sweden"]

    radius_meters = 50000

    scanner = RadarCoverage(sweden, radius_meters)
    result = scanner.scan()
    print(len(result))

Clarkin

Answer 5

I wrote a greedy algorithm: Pick a first point in the polygon, generate the circle, subtract the circle from the polygon. Repeat until none of the polygon is left.

It’s certainly not optimal, but it’s quick to implement and works with irregularly formed polygons and multipolygons as well.

Implementation in Python using GeoPandas and Shapely:

import geopandas as gpd
import pyproj
import shapely

def radius_covering(area_4326: gpd.GeoDataFrame, radius_meter: float, meter_crs):
    wgs84 = pyproj.CRS('EPSG:4326')
    meter_proj = pyproj.CRS(meter_crs)
    meter_to_wgs84 = pyproj.Transformer.from_crs(meter_proj, wgs84, always_xy=True).transform

    area_projected = area_4326.to_crs(meter_crs)
    remaining_area = area_projected.iloc[0].geometry
    while remaining_area.area > 0:
        remaining_buffered = remaining_area.buffer(-radius_meter / 3)
        use_for_border = remaining_buffered if remaining_buffered.area > 0 else remaining_area
        if use_for_border.geom_type == 'MultiPolygon':
            center = use_for_border.geoms[0].exterior.interpolate(0)
        else:
            center = use_for_border.exterior.interpolate(0)
        center_point = shapely.geometry.Point(center)
        center_wgs84 = shapely.ops.transform(meter_to_wgs84, center_point)
        yield center_wgs84
        circle = center_point.buffer(radius_meter)
        remaining_area = remaining_area.difference(circle)

Confute

Can you expand on this code - how does it produce the image in the answer? – Clarkin