How to compute a minimum bottleneck spanning tree in linear time?

Question

We can find a minimum bottleneck spanning tree in O(E log*V) in the worst case by using Kruskal's algorithm. This is because every minimum spanning tree is a minimum bottleneck spanning tree.

But I got stuck on this job-interview question from this course.

How can we find a minimum bottleneck spanning tree in linear time even in the worst case. Note that we can assume that we can compute the median of n keys in linear time in the worst case.

Ophthalmoscope

Use binary search. The log factor goes away with a little optimization. – Ruination

@DavidEisenstat I have thought about binary searching the answer. But how can you optimize the search. To check whether the current guess is correct, you will need a dfs which will in turn take linear time. – Ophthalmoscope

Answer 1

1. Get V, the median of the weights of the |E| edges.
2. Find all edge's value no more than V, and get the subgraph
   • If the subgraph is connected, V is the upper limit of the answer, and decrease the V, repeat the step 1, 2.
   • If the subgraph is not connected, let the connected component to become a node, and increase the V, repeat the step 1, 2.

Then you can solve the question in linear time.

PS: Using DFS to judge the subgraph is connected. and the complexity is O(E/2) + O(E/4) + O(E/8) + ... = O(E)

Mulford

+1. It's a bit confusing that you use the notation V for the value of the bottleneck, when the question (and convention) uses it for the (number of) vertices. :-) But that aside, I think in step 1 you mean "Get V, the median of the weights of the |E| edges, ...". – Eatmon

1.How do you find the median of the weights of |E| edges in linear time? 2.Could you please be more specific about "increasing" or "decreasing" v? – Kamp

You can find linear time median find algorithm in literature. One developed by M. Blum (divide and conquer algorithm by taking group of 5). – Ballista

how are we sure that contracting the connected components to nodes won't disrupt our ability to find a true bottleneck spanning tree? – Aberdare

Answer 2

The standard algorithm for finding Minimum Bottleneck Spanning Tree (MBST) is known as Camerini’s algorithm. It runs in linear time and is as follows:

 1. Find a median edge weight in graph and partition all edges in to two
    partitions A and B around it. Let A have all edges greater than
    pivot and B has all edges less than or equal to pivot.                
 2. Run DFS or BFS on partition B. If it connected graph then again run
    step 1 on it.        
 3. If partition B wasn't a connected graph then we must have more than
    1 connected components in it. Create a new graph by contracting each
    of these connected components as a single vertex and select edges
    from partition A that connects these components. MBST is given by
    edges in connected components + MBST of new graph.

In pseudo-code:

1:  procedure MBST(V, E)
2:      if |E| = 1 then
3:          Return E 
4:      else
5:          A, B ←  Partition E in two halves around median
6:                  A is higher half, B is lower half
7:          F ← Connected components of B
8:          if |F| = 1 and spans all vertices then
9:              Return MBST(V, B)
10:         else
11:             V' ← create one vertex for each connected component in F
12:                     plus vertices missing from F
13:             B' ← Edges from A that connects components in F
14:                     and edges to vertices not in F
15:             Return F ∪ MBST(V', B') 
16:         end if
17:     end if
18: end procedure

Implementation notes:

1. Median can be found in O(n).
2. Line 7 can generate disjoint-set data structure using BFS or DFS.
3. Line 13 involves filtering out edges in A where each edge has endpoints that are either in two different connected components in F or one endpoint is vertex not in F and other is in F or both are not in F. This tests can be done using efficient disjoint-set data structure in O(1) amortized time for each edge.

Update: I've now also created Wikipedia page on this topic.

Gigolo

This seems to forget as does wikipedia to mention that if there are multiple edges in A which go from the same non-F node to the same component in F. The minimum value should be taken and this is a very important detail if actually trying to implement this. Its intuitive as there is basically no other choice. Otherwise, you get multiple edges with multiple costs and it creates real complications. It also reduced the number of edges even more practically speaking. – Peanut

Answer 3

I found the other answers lacking detail, confusing or plain wrong. For example, ShitalShah's answer states:

Create a new graph by contracting each of these connected components as a single vertex and select edges from partition A that connects these components

Then in his pseudocode later:

11:             V' ← create one vertex for each connected component in F
12:                     plus vertices missing from F
13:             B' ← Edges from A that connects components in F
14:                     and edges to vertices not in F

"vertices missing from F" or "edges to vertices not in F" is not mentioned in the description immediately preceding the pseudocode. If we let that slide, we soon find more discrepancies:

Line 13 involves filtering out edges in A where each edge has endpoints that are either in two different connected components in F or one endpoint is vertex not in F and other is in F or both are not in F.

What? Description and pseudocode were talking about connecting the different connected components using the larger edges, and now we are suddenly filtering them out???

There's more: The link to the actual algorithm returns a 403 forbidden. The Wikipedia article is fraught with similar discrepancies. How do we create a super vertex when they completely degenerate into one vertex per connected component? How to handle parallel edges from partition A after contraction-which one should we choose? $&T^$#)*)

I believe when attempting to provide an answer, we should assume that the reader knows where we live. Thus I present working code, probably the only one found on the web. Drumroll.

public class MBST<E> {
    private static final NumberFormat formatter = NumberFormat.getNumberInstance(Locale.ENGLISH);

    static {
        formatter.setMinimumFractionDigits(2);
        formatter.setMaximumFractionDigits(2);
    }

    private final UndirectedGraph<E> mbst;

    public MBST(UndirectedGraph<E> g) {
        System.out.printf("Graph:%n%s", g);

        if (g.numEdges() <= 1) {
            mbst = g;
            return;
        }

        // can we calculate mean more efficiently?
        DoubleSummaryStatistics stats = g.edges().stream()
                .collect(summarizingDouble(e -> e.weight));
        System.out.printf("Mean: %s%n", formatter.format(stats.getAverage()));
        Map<Boolean, List<Edge<E>>> edgeMap = g.edges().stream()
                .collect(groupingBy(e -> e.weight < stats.getAverage()));

        List<Edge<E>> f = edgeMap.getOrDefault(true, emptyList());
        if (f.isEmpty()) {
            mbst = g;
            return;
        }

        UndirectedGraph<E> b = new UndirectedGraph<>(f);
        ConnectedComponents<E> cc = new ConnectedComponents<>(b);

        if (cc.size == 1 && b.numVertices() == g.numVertices()) {
            mbst = new MBST<>(b).mbst;
            return;
        }

        Map<Edge<E>, Edge<E>> bPrime = new HashMap<>();
        edgeMap.get(false)
                .forEach(e1 -> {
                    boolean vInB = b.containsVertex(e1.v);
                    boolean wInB = b.containsVertex(e1.w);
                    boolean edgeInB = vInB && wInB;
                    E v = vInB ? cc.id(e1.v) : e1.v;
                    E w = wInB ? cc.id(e1.w) : e1.w;

                    Edge<E> e2 = new Edge<>(v, w);

                    bPrime.compute(e2, (key, val) -> {
                        // same connected component
                        if (edgeInB && v.equals(w)) return null;
                        if (val == null || val.weight > e1.weight) return e1;
                        return val;
                    });
                });
        mbst = new MBST<>(new UndirectedGraph<>(bPrime.values())).mbst;
        for (Edge<E> e : f) mbst.addEdge(e);
    }

    public Iterable<Edge<E>> edges() {
        return mbst.edges();
    }
}

I tested it against the following graphs. The first image is from the Wikipedia article, the second from this paper.

Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (B, C), (D, E), (E, F), (F, G), (B, D), (C, E), (D, F), (E, G), (A, D), (B, E)]
Mean: 8.00
Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (C, E), (D, F), (E, G), (A, D), (B, E)]
Mean: 6.17
Graph:
Vertices = [A, B, E, G]
Edges = [(A, B), (E, G), (B, E)]
Mean: 7.00

Graph:
Vertices = [A, B, C, D, E, F, G]
Edges = [(A, B), (B, C), (C, D), (D, E), (F, G), (C, E), (D, F), (E, G), (B, G)]
Mean: 10.67
Graph:
Vertices = [E, G]
Edges = [(E, G)]

Unanimous

Answer 4

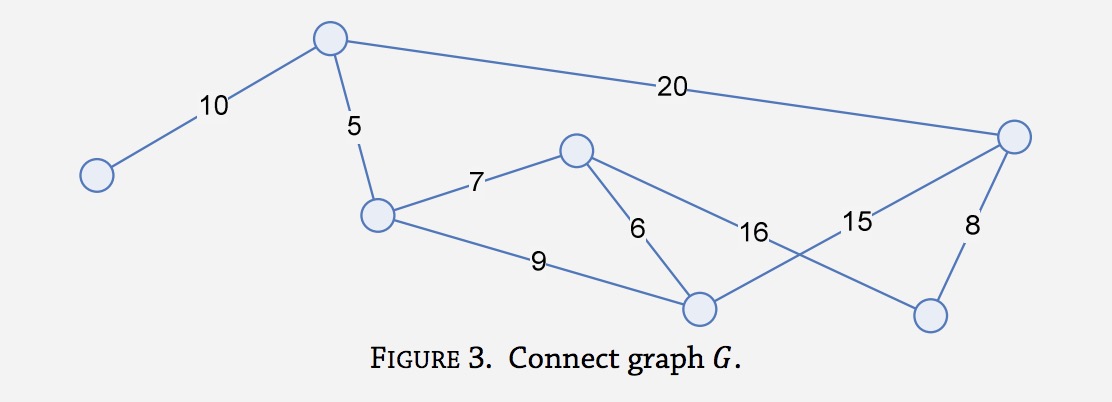
Important to note that the solution code in another answer here is incorrect. It does not only fail to get the linear time by using the median of medians algorithm which is strictly required for such time complexity, but it uses average instead of median and divides the list into potentially unequal parts which could cause an infinite loop or O(mn) time and both of which violate the assumptions of Camerini's original algorithm. Very limited test cases are not adequate to prove such an algorithm works, it takes a good amount of them before empirical verification can be considered adequate.

Here is Python code which will solve the problem using Camerini's algorithm with proper time complexity. The median of medians algorithm is quite long but the only way to achieve it. The Wikipedia example as well as a visualization function using graphviz is provided. It is assumed you are talking about undirected graphs per the question referencing Kruskal with O(m log n). Some unnecessary adjacency matrix to edge list conversions which is O(n^2) is here but it can be easily optimized out.

def adj_mat_to_edge_list(adj_mat):
    #undirected graph needs reflexivity check
    return {i+1:[j+1 for j, y in enumerate(row) if not y is None or not adj_mat[j][i] is None]
            for i, row in enumerate(adj_mat)}
def adj_mat_to_costs(adj_mat):
    return {(i+1, j+1): adj_mat[i][j] for i, row in enumerate(adj_mat)
            for j, y in enumerate(row) if not y is None or not adj_mat[j][i] is None}
def partition5(l, left, right):
    i = left + 1
    while i <= right:
        j = i
        while j > left and l[j-1] > l[j]:
            l[j], l[j-1] = l[j-1], l[j]
            j -= 1
        i += 1
    return (left + right) // 2
def pivot(l, left, right):
    if right - left < 5: return partition5(l, left, right)
    for i in range(left, right+1, 5):
        subRight = i + 4
        if subRight > right: subRight = right
        median5 = partition5(l, i, subRight)
        l[median5], l[left + (i-left) // 5] = l[left + (i-left) // 5], l[median5]
    mid = (right - left) // 10 + left + 1
    return medianofmedians(l, left, left + (right - left) // 5, mid)
def partition(l, left, right, pivotIndex, n):
    pivotValue = l[pivotIndex]
    l[pivotIndex], l[right] = l[right], l[pivotIndex]
    storeIndex = left
    for i in range(left, right):
        if l[i] < pivotValue:
            l[storeIndex], l[i] = l[i], l[storeIndex]
            storeIndex += 1
    storeIndexEq = storeIndex
    for i in range(storeIndex, right):
        if l[i] == pivotValue:
            l[storeIndexEq], l[i] = l[i], l[storeIndexEq]
            storeIndexEq += 1
    l[right], l[storeIndexEq] = l[storeIndexEq], l[right]
    if n < storeIndex: return storeIndex
    if n <= storeIndexEq: return n
    return storeIndexEq
def medianofmedians(l, left, right, n):
    while True:
        if left == right: return left
        pivotIndex = pivot(l, left, right)
        pivotIndex = partition(l, left, right, pivotIndex, n)
        if n == pivotIndex: return n
        elif n < pivotIndex: right = pivotIndex - 1
        else: left = pivotIndex + 1
def bfs(g, s):
    n, L = len(g), {}
    #for i in range(1, n+1): L[i] = 0
    L[s] = None; S = [s]
    while len(S) != 0:
        u = S.pop(0)
        for v in g[u]:
            if not v in L: L[v] = u; S.append(v)
    return L
def mbst(g, costs):
    if len(g) == 2 and len(g[next(iter(g))]) == 1: return g
    l = [(costs[(x, y)], (x, y)) for x in g for y in g[x] if x < y]
    medianofmedians(l, 0, len(l) - 1, len(l) // 2)
    A, B = l[len(l)//2:], l[:len(l)//2]
    Gb = {}
    for _, (x, y) in B:
        if x > y: continue
        if not x in Gb: Gb[x] = []
        if not y in Gb: Gb[y] = []
        Gb[x].append(y)
        Gb[y].append(x)
    F, Fr, S = {}, {}, set(Gb)
    while len(S) != 0:
        C = set(bfs(Gb, next(iter(S))))
        S -= C
        root = next(iter(C))
        F[root] = C
        for x in C: Fr[x] = root
    if len(F) == 1 and len(Fr) == len(g): return mbst(Gb, costs)
    else:
        Ga, ca, mp = {}, {}, {}
        for _, (x, y) in A:
            if x > y or (x in Fr and y in Fr): continue
            if x in Fr:
                skip = (Fr[x], y) in ca
                if not skip or ca[(Fr[x], y)] > costs[(x, y)]:
                    ca[(Fr[x], y)] = ca[(y, Fr[x])] = costs[(x, y)]
                if skip: continue
                mp[(Fr[x], y)] = (x, y); mp[(y, Fr[x])] = (y, x)
                x = Fr[x]
            elif y in Fr:
                skip = (x, Fr[y]) in ca
                if not skip or ca[(x, Fr[y])] > costs[(x, y)]:
                    ca[(x, Fr[y])] = ca[(Fr[y], x)] = costs[(x, y)]
                if skip: continue
                mp[(x, Fr[y])] = (x, y); mp[(Fr[y], x)] = (y, x)
                y = Fr[y]
            else: ca[(x, y)] = ca[(y, x)] = costs[(x, y)]
            if not x in Ga: Ga[x] = []
            if not y in Ga: Ga[y] = []
            Ga[x].append(y)
            Ga[y].append(x)
        res = mbst(Ga, ca)
        finres = {}
        for x in res:
            for y in res[x]:
                if x > y: continue
                if (x, y) in mp: x, y = mp[(x, y)]
                if not x in finres: finres[x] = []
                if not y in finres: finres[y] = []
                finres[x].append(y)
                finres[y].append(x)
        for x in Gb:
            for y in Gb[x]:
                if x > y: continue
                if not x in finres: finres[x] = []
                if not y in finres: finres[y] = []
                finres[x].append(y)
                finres[y].append(x)
        return finres
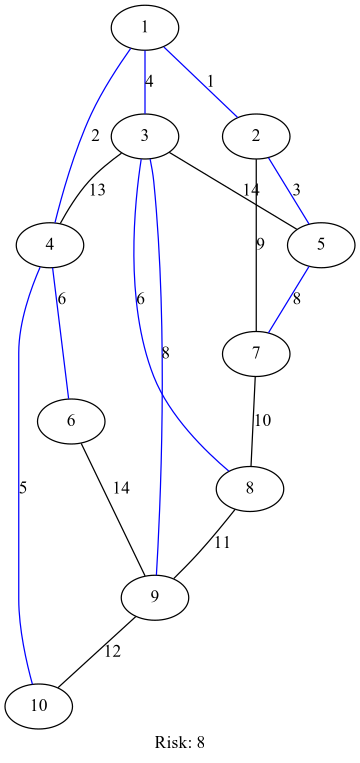
def camerini(adjmat):
    g = mbst(adj_mat_to_edge_list(riskadjmat), adj_mat_to_costs(riskadjmat))
    return {x-1: y-1 if not y is None else y for x, y in bfs(g, next(iter(g))).items()}
def operation_risk(riskadjmat):
    mst = camerini(riskadjmat)
    return max(riskadjmat[mst[x]][x] for x in mst if not mst[x] is None), mst
def risk_graph(adjmat, sr):
    risk, spantree = sr
    return ("graph {" +
            "label=\"Risk: " + str(risk) + "\"" +
            ";".join(str(i+1) + "--" + str(j+1) + "[label=" + str(col) +
                                (";color=blue" if spantree[i] == j or spantree[j] == i else "") + "]"
                                for i, row in enumerate(adjmat) for j, col in enumerate(row) if i < j and not col is None) + "}")
riskadjmat = [[None, 1, 4, 2, None, None, None, None, None, None],
            [1, None, None, None, 3, None, 9, None, None, None],
            [4, None, None, 13, 14, None, None, 6, 8, None],
            [2, None, 13, None, None, 6, None, None, None, 5],
            [None, 3, 14, None, None, None, 8, None, None, None],
            [None, None, None, 6, None, None, None, None, 14, None],
            [None, 9, None, None, 8, None, None, 10, None, None],
            [None, None, 6, None, None, None, 10, None, 11, None],
            [None, None, 8, None, None, 14, None, 11, None, 12],
            [None, None, None, 5, None, None, None, None, 12, None]]
import graphviz
graphviz.Source(risk_graph(riskadjmat, operation_risk(riskadjmat)))

Peanut