How to find the nearest line segment to a specific point more efficently?

Question

This is a problem I came across frequently and I'm searching a more effective way to solve it. Take a look at this pics:

Let's say you want to find the shortest distance from the red point to a line segment a_n. Assume you only know the start/end point (x,y) of the segments and the point. Now this can be done in O(n), where n are the line segments, by checking every distance from the point to a line segment. This is IMO not effective, because in the worst case there have to be n-1 distance checks till the right one is found.

This can be a real performance issue for n = 1000 f.e. (which is a likely number), especially if the distance calculation isn't just done in the euclidean space by the Pythagorean theorem but for example by a geodesic method like the haversine formula or Vincenty's.

This is a general problem in different situations:

• Is the point inside a radius of the vertices?
• Which set of vertices is nearest to the point?
• Is the point surrounded by line segments?

To answer these questions, the only approach I know is O(n). Now I would like to know if there is a data structure or a different strategy to solve these problems more efficiently?

To make it short: I'm searching a way, where the line segments / vertices could be "filtered" somehow to get a set of potential candidates before I start my distance calculations. Something to reduce the complexity to O(m) where m < n.

Amateur

There might be some efficiencies in checking individual line segments, such as when they share end points with other line segments, but I believe you'll always have to check all line segments, so the answer will always be order n. – Beforehand

This might be useful - en.wikipedia.org/wiki/Point_location . This for point queries, but you might be able to adapt it to your purpose – Airship

This is not a graph-theoretic problem, it belongs to the field of computational geometry. I updated the tag. – Trisaccharide

you could look into something like quad-trees in order to try and quickly cull a number of line segments that are too far away to be the "closest", although this approach might be more costly to run if n in small, or all the lines are tightly packed – Shaer

Something to keep in mind is that this problem is highly parallelizable. If your input is on the order of n=1000, the problem is effectively O(1) time complexity if executed on a GPU. – Overdose

@Overdose I already do parallel execution. But the overall performance could be increased if the right structure will be selected. – Amateur

Answer 1

Probably not an acceptable answer, but too long for a comment: The most appropriate answer here depends on details that you did not state in the question.

If you only want to perform this test once, then there will be no way avoid a linear search. However, if you have a fixed set of lines (or a set of lines that does not change too significantly over time), then you may employ various techniques for accelerating the queries. These are sometimes referred to as Spatial Indices, like a Quadtree.

You'll have to expect a trade-off between several factors, like the query time and the memory consumption, or the query time and the time that is required for updating the data structure when the given set of lines changes. The latter also depends on whether it is a structural change (lines being added or removed), or whether only the positions of the existing lines change.

Hereditament

So, the data will stay fixed just the position of the red dot is changing. Means, I build the data once, make some calculations and load a new set of data. It's likely that using a more complex data structure will be efficent, if it can reduce the overall performance through cheap query complexity. But of course I have to test it. – Amateur

Answer 2

6k views and no answer with code example. I've worked exactly on this problem so I thought I should bring this back from the dead to help you next person who stumbles upon this;

Marco13's answer was the way to go; using a Quadtree.

(My work is based off of https://github.com/Josephbakulikira/QuadTree-Visualization-with-python--pygame)

I implemented a Quadtree in python, so I could check streets closest to specific addresses on a map database. I think this represents pretty much what the OP wanted to do.

My quadtree takes in lines segments, and points. Which are in my case road segments, and house locations.

I can then query the quadtree at a specific point with a certain radius, to pick road segments close to this point, and get the closest segment.

Here is the code:

quadtree.py:

from shapes import Rectangle, Vector2, Line, Circle

class QuadTree:
    """
    Python representation of a QuadTree
    """
    def __init__(self, capacity : int, boundary : Rectangle) -> None:
        self.capacity : int = capacity
        self.boundary : Rectangle = boundary
        self.elements = set([])

        self.northWest : QuadTree = None
        self.northEast : QuadTree = None
        self.southWest : QuadTree = None
        self.southEast : QuadTree = None
        return

    @property
    def children(self) -> list | bool:
        """
        Checker if tree has children.
        If yes, returns them in list
        """
        if self.northWest != None:
            return [self.northWest, self.northEast, self.southWest, self.southEast]
        else:
            return False
    
    def subdivide(self) -> None:
        """
        Divide current tree into quadrants (children)
        """
        parent = self.boundary

        differencex = (parent.bottomRight.x - parent.topLeft.x) / 2
        differencey = (parent.bottomRight.y - parent.topLeft.y) / 2
        
        # Setup children boundaries
        boundary_nw = Rectangle(
                Vector2(parent.topLeft.x , parent.topLeft.y),
                Vector2(parent.bottomRight.x - differencex, parent.bottomRight.y - differencey)
            )
        boundary_ne = Rectangle(
                Vector2(parent.topLeft.x + differencex, parent.topLeft.y),
                Vector2(parent.bottomRight.x, parent.bottomRight.y - differencey)
            )
        boundary_sw = Rectangle(
                Vector2(parent.topLeft.x, parent.topLeft.y + differencey),
                Vector2(parent.topLeft.x + differencex, parent.bottomRight.y)
            )
        boundary_se = Rectangle(
                Vector2(parent.topLeft.x + differencex, parent.topLeft.y + differencey),
                Vector2(parent.bottomRight.x, parent.bottomRight.y)
            )

        self.northWest = QuadTree(self.capacity, boundary_nw)
        self.northEast = QuadTree(self.capacity, boundary_ne)
        self.southWest = QuadTree(self.capacity, boundary_sw)
        self.southEast = QuadTree(self.capacity, boundary_se)

        # Add parent's elements to children
        for element in self.elements:
            self.insertinchildren(element)
        
        # Clear elements from parent once they are added to children
        self.elements = set([])
        return

    def insert(self, element) -> bool:
        """
        Insert element into tree.
        If tree is at max capacity, subdivide it, and add elements to children
        """
        if self.boundary.containsElement(element) == False:
            return False

        if len(self.elements) < self.capacity and not self.children:
            self.elements.add(element)
            return True
    
        else:
            if len(self.elements) == self.capacity and not self.children:
                if type(element) == Line:
                    if element in self.elements:
                        return True
            
            if not self.children:
                self.subdivide()

            return self.insertinchildren(element)
    
    def insertinchildren(self, element) -> bool:
        """
        Insert element into children
        (Insert lines everywhere they intersect, while
         inserting points(Vectors) only in one quadrant they are in)
        """
        if isinstance(element, Line):
            self.northWest.insert(element)
            self.northEast.insert(element)
            self.southWest.insert(element)
            self.southEast.insert(element)
            return True
        else:
            if not self.northWest.insert(element):
                if not self.northEast.insert(element):
                    if not self.southWest.insert(element):
                        if not self.southEast.insert(element):
                            return False
            return True
        
    def query(self, _range : Rectangle | Circle) -> set:
        """
        Use a circle or rectangle to query the tree for
         elements in range
        """
        elements_in_range = set([])
        if _range.intersects(self.boundary):
            if self.children:
                elements_in_range.update(self.northWest.query(_range))
                elements_in_range.update(self.northEast.query(_range))
                elements_in_range.update(self.southWest.query(_range))
                elements_in_range.update(self.southEast.query(_range))
                    
            else:
                for element in self.elements:
                    if _range.containsElement(element):
                        elements_in_range.add(element)
        return elements_in_range

shapes.py

import numpy as np

class Vector2(np.ndarray):
    """
    Numpy array subclass to represent a 2D vector
    """
    def __new__(cls, x, y) -> np.ndarray:
        return np.array([x, y]).view(cls)

    @property
    def x(self) -> float:
        return self[0]
    
    @property
    def y(self) -> float:
        return self[1]
    
    def __hash__(self) -> int:
        return id(self)
    
    def __eq__(self, other) -> bool:
        if not isinstance(other, Vector2):
            return False
        return np.array_equal(self, other)
    
class Line:
    """
    Representation of a line segment
    """
    def __init__(self, point1 : Vector2, point2 : Vector2) -> None:
        self.a = point1
        self.b = point2
        return

    def __str__(self) -> str:
        return f"Line({self.a}, {self.b})"
    
    def distancetoPoint(self, p : Vector2) -> float:
        """
        Get the shortest distance between point p and the line segment
        """
        # Distance between the closest point and the point p
        return np.linalg.norm(self.closestPoint(p) - p)

    def closestPoint(self, p : Vector2) -> float:
        """
        Get the closest point on the line segment from point p
        """
        a = self.a
        b = self.b
        cp = None # Closest point
        ab = b - a
        ap = p - a
        proj = np.dot(ap, ab)
        abLenSq = ab[0]**2 + ab[1]**2
        normalizedProj = proj / abLenSq

        if normalizedProj <= 0:
            cp = a
        elif normalizedProj >= 1:
            cp = b
        else:
            cp = a + normalizedProj * ab
        return cp

     
    def onSegment(self, p, q, r) -> bool:
        """
        Given three collinear points p, q, r, the function checks if  
        point q lies on line segment 'pr' 
        """
        if ( (q.x <= max(p.x, r.x)) and (q.x >= min(p.x, r.x)) and 
            (q.y <= max(p.y, r.y)) and (q.y >= min(p.y, r.y))): 
            return True
        return False

    def orientation(self, p, q, r) -> int: 
        """
        To find the orientation of an ordered triplet (p,q,r) 
        function returns the following values: 
        0 : Collinear points 
        1 : Clockwise points 
        2 : Counterclockwise 
        
        See https://www.geeksforgeeks.org/orientation-3-ordered-points/amp/  
        for details of below formula.
        """  
        val = (float(q.y - p.y) * (r.x - q.x)) - (float(q.x - p.x) * (r.y - q.y)) 
        if (val > 0): 
            # Clockwise orientation 
            return 1
        elif (val < 0): 
            # Counterclockwise orientation 
            return 2
        else: 
            # Collinear orientation 
            return 0
    
    def intersects(self, p1 : Vector2, p2 : Vector2) -> bool:
        """
        Check if current line intersects with another line 
        made of point1 and point2
        """ 
        # Find the 4 orientations required for  
        # the general and special cases 
        o1 = self.orientation(self.a, self.b, p1) 
        o2 = self.orientation(self.a, self.b, p2) 
        o3 = self.orientation(p1, p2, self.a) 
        o4 = self.orientation(p1, p2, self.b) 
    
        # General case 
        if ((o1 != o2) and (o3 != o4)): 
            return True
    
        # _____________ Special Cases _____________ 
        # self.a , self.b and p1 are collinear and p1 lies on segment p1q1 
        if ((o1 == 0) and self.onSegment(self.a, p1, self.b)): 
            return True
    
        # self.a , self.b and p2 are collinear and p2 lies on segment p1q1 
        if ((o2 == 0) and self.onSegment(self.a, p2, self.b)): 
            return True
    
        # p1 , p2 and self.a are collinear and self.a lies on segment p2q2 
        if ((o3 == 0) and self.onSegment(p1, self.a, p2)): 
            return True
    
        # p1 , p2 and self.b are collinear and self.b lies on segment p2q2 
        if ((o4 == 0) and self.onSegment(p1, self.b, p2)): 
            return True
    
        # If none of the cases 
        return False

class Rectangle:
    """
    Rectangle used as boundaries for the QuadTree
    or as a query range for the QuadTree
    """
    def __init__(self, topLeft : Vector2, bottomRight : Vector2) -> None:
        self.topLeft = topLeft
        self.bottomRight = bottomRight
        self.topRight = Vector2(self.bottomRight.x, self.topLeft.y)
        self.bottomLeft = Vector2(self.topLeft.x, self.bottomRight.y)
        self.center = (self.topLeft + self.bottomRight) / 2
        self.top = Line(self.topLeft, Vector2(self.bottomRight.x, self.topLeft.y))
        self.bottom = Line(Vector2(self.topLeft.x, self.bottomRight.y), self.bottomRight)
        self.left = Line(self.topLeft, Vector2(self.topLeft.x, self.bottomRight.y))
        self.right = Line(Vector2(self.bottomRight.x, self.topLeft.y), self.bottomRight)
        return

    def __str__(self) -> str:
        return f"Rectangle({self.topLeft}, {self.bottomRight})"

    def containsElement(self, element : Vector2 | Line) -> bool:
        """
        Checks if the element is contained by this rectangle
        """
        if isinstance(element, Line):
            return self.containsLine(element)
        x, y = element
        bx , by = self.topLeft
        cx, cy = self.bottomRight

        if x >= bx and x <= cx and y >= by and y <= cy:
            return True
        else:
            return False
   
    def containsLine(self, line : Line) -> bool:
        """
        Checks if the line goes through this rectangle
        """
        # Check if any end of the line is inside the rectangle
        if self.containsElement(line.a) or self.containsElement(line.b):
            return True
        # Check if line intersects with any side of the rectangle
        else:
            if not line.intersects(self.top.a, self.top.b):
                if not line.intersects(self.bottom.a, self.bottom.b):
                    if not line.intersects(self.left.a, self.left.b):
                        if not line.intersects(self.right.a, self.right.b):
                            return False
            return True
    
    def intersects(self, other : 'Rectangle') -> bool:
        """
        Check if this rectangle intersects with another rectangle
        ie. if any of the sides of the rectangle crosses another rectangle
        """
        return not (self.bottomRight.x < other.topLeft.x
                    or self.topLeft.x > other.bottomRight.x
                    or self.bottomRight.y < other.topLeft.y
                    or self.topLeft.y > other.bottomRight.y)

class Circle:
    """
    Circle used as range to query the QuadTree
    """
    def __init__(self, center : Vector2, radius : float) -> None:
        self.center = center
        self.radius = radius
        return

    def __str__(self) -> str:
        return f"Circle({self.center}, r{self.radius})"

    def containsElement(self, element : Vector2 | Line) -> bool:
        """
        Checks if the element is contained by this circle
        """
        if isinstance(element, Line):
            return self.containsLine(element)
        dist = np.linalg.norm(self.center - element)
        if dist <= self.radius:
            return True
        else:
            return False
        
    def containsLine(self, line : Line) -> bool:
        """
        Checks if the line goes through this circle
        """
        if line.distancetoPoint(self.center) <= self.radius:
            return True
        else:
            return False

    def intersects(self, rectangle : Rectangle) -> bool:
        """
        Check if this circle intersects with a rectangle
        """
        # There are only two cases where a circle and a rectangle can intersect:
        # 1. The circle center is inside the rectangle
        if not rectangle.containsElement(self.center):
            # 2. The circle intersects with one of the rectangle's sides
            if not self.containsLine(rectangle.top):
                if not self.containsLine(rectangle.bottom):
                    if not self.containsLine(rectangle.left):
                        if not self.containsLine(rectangle.right):
                            return False
        return True

main.py

from quadtree import QuadTree
from shapes import Rectangle, Circle, Vector2, Line

# Setup lines with Overpass nodes
node0 = Vector2(107.1360616, 46.1032011)
node1 = Vector2(107.13563750000003, 46.102939)
node2 = Vector2(107.13538800000003, 46.1028447)
node3 = Vector2(107.13493060000002, 46.1027272)
node4 = Vector2(107.13318809999998, 46.1021657)
node5 = Vector2(107.13255700000002, 46.1019075)
node6 = Vector2(107.1316817, 46.1014684)
node7 = Vector2(107.13088449999998, 46.1011467)
node8 = Vector2(107.1304002, 46.1010027)
node9 = Vector2(107.1299055, 46.1009219)
node10 = Vector2(107.12915320000002, 46.1008729)
node11 = Vector2(107.12877689999999, 46.1008901)
node12 = Vector2(107.12828999999999, 46.10097)
node13 = Vector2(107.1274209, 46.1012472)
node14 = Vector2(107.1270212, 46.1014094)
node15 = Vector2(107.1265209, 46.101732)
node16 = Vector2(107.12579249999999, 46.1022694)
node17 = Vector2(107.1256219, 46.1024435)
node18 = Vector2(107.12546250000003, 46.1026809)
node19 = Vector2(107.12500690000002, 46.1034946)

nodes = [node0, node1, node2, node3, node4, node5, node6, node7, node8, node9,
         node10, node11, node12, node13, node14, node15, node16, node17, node18, node19]

lines = []
for i in range(len(nodes)-1):
    lines.append(Line(nodes[i], nodes[i+1]))


# Setup points
house0 = Vector2(107.13595197486893, 46.10285045021604)
house1 = Vector2(107.1300706177878, 46.101115083412374)
house2 = Vector2(107.13043003379954, 46.100917943095524)
house3 = Vector2(107.13046758472615, 46.101234111186926)
house4 = Vector2(107.13071434795808, 46.10100721426972)
house5 = Vector2(107.13108449280605, 46.10108904605243)
house6 = Vector2(107.12480471447458, 46.10391049893959)
house7 = Vector2(107.12635081112013, 46.10232085692584)

houses = [house0, house1, house2, house3, house4, house5, house6, house7]

# Setup quadtree
tree = QuadTree(2, Rectangle(Vector2(107.12383, 46.09690), Vector2(107.13709, 46.10700)))
for l in lines:
    tree.insert(l)

for h in houses:
    tree.insert(h)

# Setup query
queryAT = Vector2(107.12739, 46.10358)
radQuery = Circle(queryAT, 0.0022)


found_elements = tree.query(radQuery)
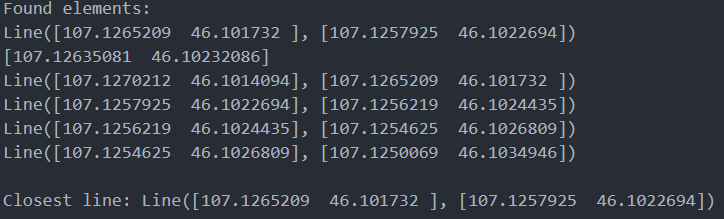
print("Found elements:")
for element in found_elements:
    print(element)

# Find closest line
shortest_dist = 999999
closest_line = None
for element in found_elements:
    if isinstance(element, Line):
        dist = element.distancetoPoint(queryAT)
        if dist < shortest_dist:
            shortest_dist = dist
            closest_line = element
print("\nClosest line: " + str(closest_line))

# ----------   Represent everything in a graph ------------
import matplotlib.pyplot as plt
import matplotlib.patches as patches

fig, ax = plt.subplots()
ax.set_xlim(tree.boundary.topLeft.x, tree.boundary.bottomRight.x)
ax.set_ylim(tree.boundary.topLeft.y, tree.boundary.bottomRight.y)

def plot_tree(ax, quadtree):
    """
    Traverse the quadtree recursively and
     plot the boundaries and elements of each node
    """
    if quadtree.children:
        for child in quadtree.children:
            plot_tree(ax, child)
    else:
        ax.add_patch(patches.Rectangle((quadtree.boundary.topLeft.x, quadtree.boundary.topLeft.y), quadtree.boundary.bottomRight.x-quadtree.boundary.topLeft.x, quadtree.boundary.bottomRight.y - quadtree.boundary.topLeft.y, fill=False))
        for element in quadtree.elements:
            clr = 'black'
            if element in found_elements:
                clr = 'magenta'
            if element is closest_line:
                clr = 'red'
            if isinstance(element, Line):
                ax.plot([element.a.x, element.b.x], [element.a.y, element.b.y], color=clr)
                #plot end segments as dots:
                ax.plot(element.a.x, element.a.y, 'o', color=clr)
                ax.plot(element.b.x, element.b.y, 'o', color=clr)
            elif isinstance(element, Vector2):
                ax.plot(element.x, element.y, 'go')
    return

plot_tree(ax, tree)

# Add query circle to plot
ax.add_patch(patches.Circle((queryAT.x, queryAT.y), radQuery.radius, fill=False, color='orange'))
# add circle center to plot
ax.plot(queryAT.x, queryAT.y, 'o', color='orange')

ax.set_box_aspect(1) # make the plot square
plt.show()

So in main.py I use coordinates points and setup a Quadtree of an area of approx. 1km square with only one street made of several line segments.

I then query a specific spot (107.12739, 46.10358) lon,lat , at a distance of 0.0022 = around 170meters

This gives me the results:

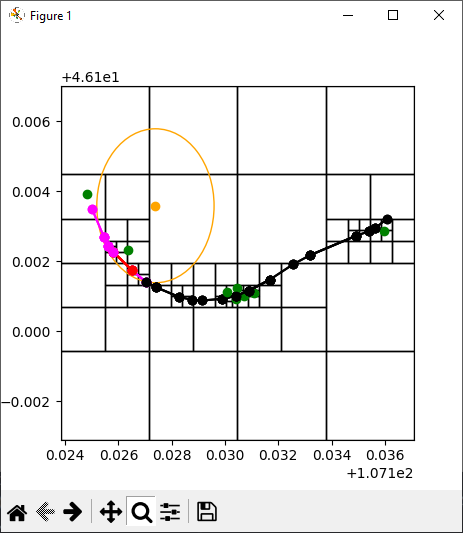
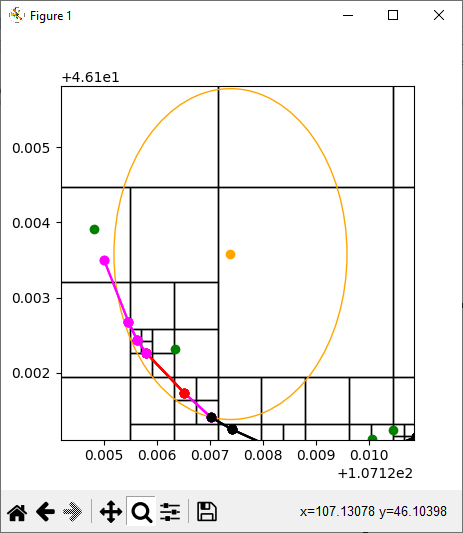
Visualization in matplotlib: Orange is the query circle Magenta are the segments found by the query The red line is the closest line

Is it really more efficient for 1000 segments? I don't know. Anyway, there you go.

Jaimeejaimes