I'm trying to write a program that calculates decimal digits of π to 1000 digits or more.
To practice low-level programming for fun, the final program will be written in assembly, on a 8-bit CPU that has no multiplication or division, and only performs 16-bit additions. To ease the implementation, it's desirable to be able to use only 16-bit unsigned integer operations, and use an iterative algorithm. Speed is not a major concern. And fast multiplication and division is beyond the scope of this question, so don't consider those issues as well.
Before implementing it in assembly, I'm still trying to figure out an usable algorithm in C on my desktop computer. So far, I found the following series is reasonably efficient and relatively easy to implement.
The formula is derived from the Leibniz Series using a convergence acceleration technique, To derive it, see Computing the Digits in π, by Carl D. Offner (https://cs.umb.edu/~offner/files/pi.pdf), page 19-26. The final formula is shown in page 26. The initial formula I've written had some typos, please refresh the page to see the fixed formula. The constant term 2 at the greatest term is explained in page 54. The paper described an advanced iterative algorithm as well, but I didn't use it here.
If one evaluates the series using many (e.g. 5000) terms, it's possible to get thousands digits of π easily, and I found this series is easy to evaluate iteratively as well using this algorithm:
Algorithm
- First, rearrange the formula to obtain its constant terms from an array.
Fill the array with 2 to start the first iteration, hence the new formula resembles the original one.
Let
carry = 0.Start from the greatest term. Obtain one term (2) from the array, multiply the term by
PRECISIONto perform a fixed-point division against2 * i + 1, and save the reminder as the new term to the array. Then add the next term. Now decrementi, go to the next term, repeat untili == 1. Finally add the final termx_0.Because 16-bit integer is used,
PRECISIONis10, hence 2 decimal digits are obtained, but only the first digit is valid. Save the second digit as carry. Show the first digit plus carry.x_0is the integer 2, it should not be added for the successive iterations, clear it.Goto step 4 to calculate the next decimal digit, until we have all the digits we want.
Implementation 1
Translating this algorithm to C:
#include <stdio.h>
#include <stdint.h>
#define N 2160
#define PRECISION 10
uint16_t terms[N + 1] = {0};
int main(void)
{
/* initialize the initial terms */
for (size_t i = 0; i < N + 1; i++) {
terms[i] = 2;
}
uint16_t carry = 0;
for (size_t j = 0; j < N / 4; j++) {
uint16_t numerator = 0;
uint16_t denominator;
uint16_t digit;
for (size_t i = N; i > 0; i--) {
numerator += terms[i] * PRECISION;
denominator = 2 * i + 1;
terms[i] = numerator % denominator;
numerator /= denominator;
numerator *= i;
}
numerator += terms[0] * PRECISION;
digit = numerator / PRECISION + carry;
carry = numerator % PRECISION;
printf("%01u", digit);
/* constant term 2, only needed for the first iteration. */
terms[0] = 0;
}
putchar('\n');
}
The code can calculate π to 31 decimal digits, until it makes an error.
31415926535897932384626433832794
10 <-- wrong
Sometimes digit + carry is greater than 9, so it needs an extra carry. If we are very unlucky, there may even be a double carry, triple carry, etc. We use a ring-buffer to store the last 4 digits. If an extra carry is detected, we output a backspace to erase the previous digit, perform a carry, and reprint them. This is just a ugly solution to the Proof-of-Concept, which is irrelevant to my question about overflow, but for completeness, here is it. Something better would be implemented in the future.
Implementation 2 with Repeated Carry
#include <stdio.h>
#include <stdint.h>
#define N 2160
#define PRECISION 10
#define BUF_SIZE 4
uint16_t terms[N + 1] = {0};
int main(void)
{
/* initialize the initial terms */
for (size_t i = 0; i < N + 1; i++) {
terms[i] = 2;
}
uint16_t carry = 0;
uint16_t digit[BUF_SIZE];
int8_t idx = 0;
for (size_t j = 0; j < N / 4; j++) {
uint16_t numerator = 0;
uint16_t denominator;
for (size_t i = N; i > 0; i--) {
numerator += terms[i] * PRECISION;
denominator = 2 * i + 1;
terms[i] = numerator % denominator;
numerator /= denominator;
numerator *= i;
}
numerator += terms[0] * PRECISION;
digit[idx] = numerator / PRECISION + carry;
/* over 9, needs at least one carry op. */
if (digit[idx] > 9) {
for (int i = 1; i <= 4; i++) {
if (i > 3) {
/* allow up to 3 consecutive carry ops */
fprintf(stderr, "ERROR: too many carry ops!\n");
return 1;
}
/* erase a digit */
putchar('\b');
/* carry */
digit[idx] -= 10;
idx--;
if (idx < 0) {
idx = BUF_SIZE - 1;
}
digit[idx]++;
if (digit[idx] < 10) {
/* done! reprint the digits */
for (int j = 0; j <= i; j++) {
printf("%01u", digit[idx]);
idx++;
if (idx > BUF_SIZE - 1) {
idx = 0;
}
}
break;
}
}
}
else {
printf("%01u", digit[idx]);
}
carry = numerator % PRECISION;
terms[0] = 0;
/* put an element to the ring buffer */
idx++;
if (idx > BUF_SIZE - 1) {
idx = 0;
}
}
putchar('\n');
}
Great, now the program can correctly calculate 534 digits of π, until it makes an error.
3141592653589793238462643383279502884
1971693993751058209749445923078164062
8620899862803482534211706798214808651
3282306647093844609550582231725359408
1284811174502841027019385211055596446
2294895493038196442881097566593344612
8475648233786783165271201909145648566
9234603486104543266482133936072602491
4127372458700660631558817488152092096
2829254091715364367892590360011330530
5488204665213841469519415116094330572
7036575959195309218611738193261179310
5118548074462379962749567351885752724
8912279381830119491298336733624406566
43086021394946395
22421 <-- wrong
16-bit Integer Overflow
It turns out, during the calculation of the largest terms at the beginning, the error term gets quite large, since the divisors at the beginning are in the range of ~4000. When evaluating the series, numerator actually starts to overflow in the multiplication immediately.
The integer overflow is insignificant when calculating the first 500 digits, but starts to get worse and worse, until it gives an incorrect result.
Changing uint16_t numerator = 0 to uint32_t numerator = 0 can solve this problem and calculate π to 1000+ digits.
However, as I mentioned before, my target platform is a 8-bit CPU, and only has 16-bit operations. Is there a trick to solve the 16-bit integer overflow issue that I'm seeing here, using only one or more uint16_t? If it's not possible to avoid multiple-precision arithmetic, what is the simplest method to implement it here? I know somehow I need to introduce an extra 16-bit "extension word", but I'm not sure how can I implement it.
And thanks in advance for your patience to understand the long context here.

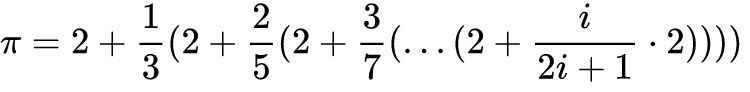

Picalculation formula? – Townsman2at the greatest term is explained in page 54. My initial formula I've written had some typos, please refresh the page to see the fixed formula. The paper described an advanced iterative algorithm as well, but I didn't use it here. – Dacosta