Why can't a LL grammar be left-recursive?

Question

In the dragon book, LL grammar is defined as follows:

A grammar is LL if and only if for any production A -> a|b, the following two conditions apply.

1. FIRST(a) and FIRST(b) are disjoint. This implies that they cannot both derive EMPTY

2. If b can derive EMPTY, then a cannot derive any string that begins with FOLLOW(A), that is FIRST(a) and FOLLOW(A) must be disjoint.

And I know that LL grammar can't be left recursive, but what is the formal reason? I guess left-recursive grammar will contradict rule 2, right? e.g., I've written following grammar:

S->SA|empty
A->a

Because FIRST(SA) = {a, empty} and FOLLOW(S) ={$, a}, then FIRST(SA) and FOLLOW(S) are not disjoint, so this grammar is not LL. But I don't know if it is the left-recursion make FIRST(SA) and FOLLOW(S) not disjoint, or there is some other reason? Put it in another way, is it true that every left-recursive grammar will have a production that will violate condition 2 of LL grammar?

Periodic

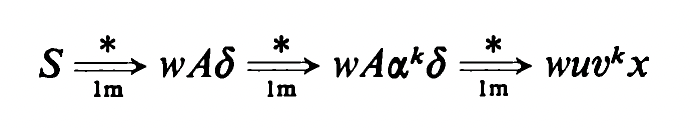
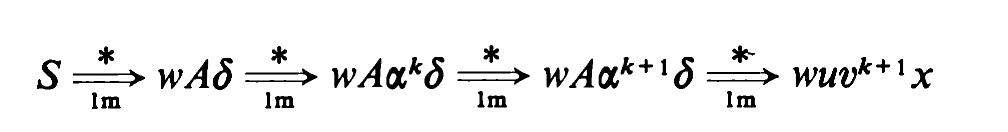
FIRST[1](SA) is {a}. – Homophile

The theoretical problem is that LA(S->SA) and LA(S->e) both contain a. See my answer for a more intuitive explanation. – Homophile

Answer 1

OK, I figure it out, if a grammar contains left-recursive production, like:

S->SA

Then somehow it must contain another production to "finish" the recursion,say:

S->B

And since FIRST(B) is a subset of FIRST(SA), so they are joint, this violates condition 1, there must be conflict when filling parse table entries corresponding to terminals both in FIRST(B) and FIRST(SA). To summarize, left-recursion grammar could cause FIRST set of two or more productions to have common terminals, thus violating condition 1.

Periodic

Answer 2

Consider your grammar:

S->SA|empty
A->a

This is a shorthand for the three rules:

S -> SA
S -> empty
A -> a

Now consider the string aaa. How was it produced? You can only read one character at a time if you have no lookahead, so you start off like this (you have S as start symbol):

S -> SA
S -> empty
A -> a

Fine, you have produced the first a. But now you cannot apply any more rules because there is no more non-terminals. You are stuck!

What you should have done was this:

S -> SA
S -> SA
S -> SA
S -> empty
A -> a
A -> a
A -> a

But you don't know this without reading the entire string. You would need an infinite amount of lookahead.

In a general sense, yes, every left-recursive grammar can have ambiguous strings without infinite lookahead. Look at the example again: There are two different rules for S. Which one should we use?

Toting

Thanks for your reply, but please understand what I am asking, yes, we can't decide which rule for S to use because FIRST(SA) and FOLLOW(S) are joint, my question is: is it left recursion that makes FIRST(SA) and FOLLOW(S) joint? Thanks. – Periodic

@Periodic Your question is specific to S->SX|e forms, and the answer would be yes. In the more general case, there will be intersection between the lookahead (LA) sets for the different rules for S if there is an S->SX. Intersections in the LA sets for the same non-terminal symbol means that a deterministic decision for the right rule cannot be made on certain input. – Homophile

Answer 3

An LL(k) grammar is one that allows the construction of a deterministic, descent parser with only k symbols of lookahead. The problem with left recursion is that it makes it impossible to determine which rule to apply until the complete input string is examined, which makes the required k potentially infinite.

Using your example, choose a k, and give the parser an input sequence of length n >= k:

aaaaaaa...

A parser cannot decide if it should apply S->SA or S->empty by looking at the k symbols ahead because the decision would depend on how many times S->SA has been chosen before, and that is information the parser does not have.

The parser would have to choose S->SA exactly n times and S->empty once, and it's impossible to decide which is right by looking at the first k symbols in the input stream.

To know, a parser would have to both examine the complete input sequence, and keep count of how many times S->SA has been chosen, but such a parser would fall outside of the definition of LL(k).

Note that unlimited lookahead is not a solution because a parser runs on limited resources, so there will always be a finite input sequence of a length large enough to make the parser crash before producing any output.

Homophile

Answer 4

In the book "The Theory of Parsing", Volume 2, by Aho and Ullman, page 681 you can find Lemma 8.3 that states: "No LL(k) grammar is left-recursive".

The proof says:

Suppose that G = (N, T, P, S) has a left-recursive nonterminal A. Then there is a derivation A -> Aw. If w -> e then it is easy to show that G is ambiguous and hence cannot be LL. Thus, assume that w -> v for some v in T+ (a non empty string of terminals). We can further assume that A -> u, being u some string of terminals and that there exists a derivation

Hence, there is another derivation:

Rhubarb