How to adjust branch lengths of dendrogram in matplotlib (like in astrodendro)? [Python]

Question

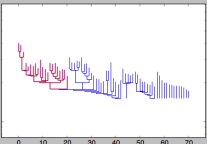
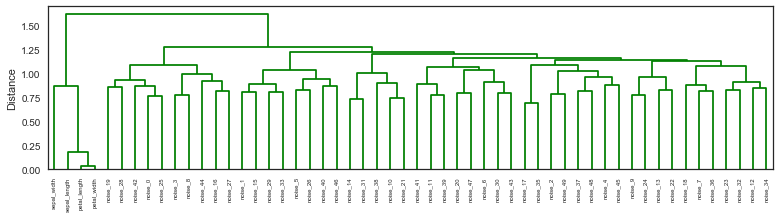
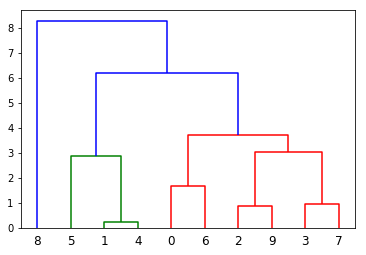
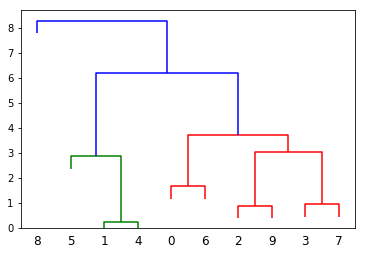
Here is my resulting plot below but I would like it to look like the truncated dendrograms in astrodendro such as this:

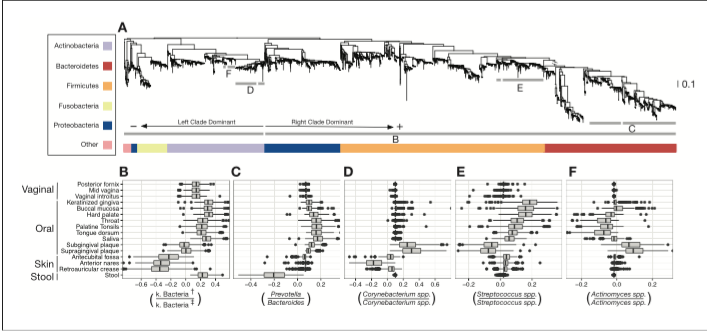
There is also a really cool looking dendrogram from this paper that I would like to recreate in matplotlib.

Below is the code for generating an iris data set with noise variables and plotting the dendrogram in matplotlib.

Does anyone know how to either: (1) truncate the branches like in the example figures; and/or (2) to use astrodendro with a custom linkage matrix and labels?

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import astrodendro
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial import distance

def iris_data(noise=None, palette="hls", desat=1):
    # Iris dataset
    X = pd.DataFrame(load_iris().data,
                     index = [*map(lambda x:f"iris_{x}", range(150))],
                     columns = [*map(lambda x: x.split(" (cm)")[0].replace(" ","_"), load_iris().feature_names)])

    y = pd.Series(load_iris().target,
                           index = X.index,
                           name = "Species")
    c = map_colors(y, mode=1, palette=palette, desat=desat)#y.map(lambda x:{0:"red",1:"green",2:"blue"}[x])

    if noise is not None:
        X_noise = pd.DataFrame(
            np.random.RandomState(0).normal(size=(X.shape[0], noise)),
            index=X_iris.index,
            columns=[*map(lambda x:f"noise_{x}", range(noise))]
        )
        X = pd.concat([X, X_noise], axis=1)
    return (X, y, c)

def dism2linkage(DF_dism, method="ward"):
    """
    Input: A (m x m) dissimalrity Pandas DataFrame object where the diagonal is 0
    Output: Hierarchical clustering encoded as a linkage matrix

    Further reading:
    http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.cluster.hierarchy.linkage.html
    https://pypi.python.org/pypi/fastcluster
    """
    #Linkage Matrix
    Ar_dist = distance.squareform(DF_dism.as_matrix())
    return linkage(Ar_dist,method=method)


# Get data
X_iris_with_noise, y_iris, c_iris = iris_data(50)
# Get distance matrix
df_dism = 1- X_iris_with_noise.corr().abs()
# Get linkage matrix
Z = dism2linkage(df_dism)

#Create dendrogram
with plt.style.context("seaborn-white"):
    fig, ax = plt.subplots(figsize=(13,3))
    D_dendro = dendrogram(
             Z, 
             labels=df_dism.index,
             color_threshold=3.5,
             count_sort = "ascending",
             #link_color_func=lambda k: colors[k]
             ax=ax
    )
    ax.set_ylabel("Distance")

Petulia

So I don't forget: github.com/dendrograms/astrodendro/blob/master/astrodendro/… I'll check out the source code for this soon. – Petulia

github.com/dendrograms/astrodendro/blob/master/astrodendro/… – Petulia

github.com/scipy/scipy/blob/v0.14.0/scipy/cluster/… note-to-self reengineer this. – Petulia

Answer 1

I'm not sure this really constitutes a practical answer, but it does allow you to generate dendrograms with truncated hanging lines. The trick is to generate the plot as normal, then manipulate the resulting matplotlib plot to recreate the lines.

I couldn't get your example to work locally, so I've just created a dummy dataset.

from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
import numpy as np

a = np.random.multivariate_normal([0, 10], [[3, 1], [1, 4]], size=[5,])
b = np.random.multivariate_normal([0, 10], [[3, 1], [1, 4]], size=[5,])
X = np.concatenate((a, b),)

Z = linkage(X, 'ward')

fig = plt.figure()
ax = fig.add_subplot(1,1,1)

dendrogram(Z, ax=ax)

The resulting plot is the usual long-arm dendrogram.

Now for the more interesting bit. A dendrogram is made up of a number of LineCollection objects (one for each colour). To update the lines we iterate through these, extracting the details about their constituent paths, modifying these to remove any lines reaching to a y of zero, and then recreating a LineCollection for these modified paths.

The updated path is then added to the axes, and the original is removed.

The one tricky part is determining what height to draw to instead of zero. Since we are iterating over each dendrograms path, we don't know which point came before — we basically have no idea where we are. However, we can exploit the fact that hanging lines hang vertically. Assuming there are no lines on the same x, we can look for the known other y values for a given x and use that as the basis for our new y when calculating. The downside is that in order to make sure we have this number, we have to pre-scan the data.

Note: If you can get dendrogram hanging lines on the same x, you would need to include the y and search for nearest y above this x to do this.

import numpy as np
from matplotlib.path import Path
from matplotlib.collections import LineCollection

fig = plt.figure()
ax = fig.add_subplot(1,1,1)

dendrogram(Z, ax=ax);

for c in ax.collections[:]: # use [:] to get a copy, since we're adding to the same list
    paths = []
    for path in c.get_paths():
        segments = []
        y_at_x = {}
        # Pre-pass over all elements, to find the lowest y value at each x value.
        # we can use this to caculate where to cut our lines.
        for n, seg in enumerate(path.iter_segments()):
            x, y = seg[0]
            # Don't store if the y is zero, or if it's higher than the current low.
            if y > 0 and y < y_at_x.get(x, np.inf):
                y_at_x[x] = y

        for n, seg in enumerate(path.iter_segments()):
            x, y = seg[0]

            if y == 0:
                # If we know the last y at this x, use it - 0.5, limit > 0
                y = max(0, y_at_x.get(x, 0) - 0.5)

            segments.append([x,y])

        paths.append(segments)

    lc = LineCollection(paths, colors=c.get_colors())  # Recreate a LineCollection with the same params
    ax.add_collection(lc)
    ax.collections.remove(c) # Remove the original LineCollection

The resulting dendrogram looks like this:

Tenstrike