Personally I would prefer a simple generator like this:
def gen(lst):
cumulative = 0
for item in lst:
if item:
cumulative += item
else:
cumulative = 0
yield cumulative
Nothing magic (when you know how yield works), easy to read and should be rather fast.
If you need more performance you could even wrap this as Cython extension type (I'm using IPython here). Thereby you lose the "easy to understand" portion and it's requiring "heavy dependencies":
%load_ext cython
%%cython
cdef class Cumulative(object):
cdef object it
cdef object cumulative
def __init__(self, it):
self.it = iter(it)
self.cumulative = 0
def __iter__(self):
return self
def __next__(self):
cdef object nxt = next(self.it)
if nxt:
self.cumulative += nxt
else:
self.cumulative = 0
return self.cumulative
Both need to be consumed, for example using list to give the desired output:
>>> list_a = [1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1]
>>> list(gen(list_a))
[1, 2, 3, 0, 1, 2, 0, 1, 0, 1, 2, 3]
>>> list(Cumulative(list_a))
[1, 2, 3, 0, 1, 2, 0, 1, 0, 1, 2, 3]
However since you asked about speed I wanted to share the results from my timings:
import pandas as pd
import numpy as np
import random
import pandas as pd
from itertools import takewhile
from itertools import groupby, accumulate, chain
def MSeifert(lst):
return list(MSeifert_inner(lst))
def MSeifert_inner(lst):
cumulative = 0
for item in lst:
if item:
cumulative += item
else:
cumulative = 0
yield cumulative
def MSeifert2(lst):
return list(Cumulative(lst))
def original1(list_a):
list_b = []
for i, x in enumerate(list_a):
if x == 0:
list_b.append(x)
else:
sum_value = 0
for j in list_a[i::-1]:
if j != 0:
sum_value += j
else:
break
list_b.append(sum_value)
def original2(list_a):
return [sum(takewhile(lambda x: x != 0, list_a[i::-1])) for i, d in enumerate(list_a)]
def Coldspeed1(data):
data = data.copy()
for i in range(1, len(data)):
if data[i]:
data[i] += data[i - 1]
return data
def Coldspeed2(data):
s = pd.Series(data)
return s.groupby(s.eq(0).cumsum()).cumsum().tolist()
def Chris_Rands(list_a):
return list(chain.from_iterable(accumulate(g) for _, g in groupby(list_a, bool)))
def EvKounis(list_a):
cum_sum = 0
list_b = []
for item in list_a:
if not item: # if our item is 0
cum_sum = 0 # the cumulative sum is reset (set back to 0)
else:
cum_sum += item # otherwise it sums further
list_b.append(cum_sum) # and no matter what it gets appended to the result
def schumich(list_a):
list_b = []
s = 0
for a in list_a:
s = a+s if a !=0 else 0
list_b.append(s)
return list_b
def jbch(seq):
return list(jbch_inner(seq))
def jbch_inner(seq):
s = 0
for n in seq:
s = 0 if n == 0 else s + n
yield s
# Timing setup
timings = {MSeifert: [],
MSeifert2: [],
original1: [],
original2: [],
Coldspeed1: [],
Coldspeed2: [],
Chris_Rands: [],
EvKounis: [],
schumich: [],
jbch: []}
sizes = [2**i for i in range(1, 20, 2)]
# Timing
for size in sizes:
print(size)
func_input = [int(random.random() < 0.75) for _ in range(size)]
for func in timings:
if size > 10000 and (func is original1 or func is original2):
continue
res = %timeit -o func(func_input) # if you use IPython, otherwise use the "timeit" module
timings[func].append(res)
%matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(1)
ax = plt.subplot(111)
baseline = MSeifert2 # choose one function as baseline
for func in timings:
ax.plot(sizes[:len(timings[func])],
[time.best / ref.best for time, ref in zip(timings[func], timings[baseline])],
label=func.__name__) # you could also use "func.__name__" here instead
ax.set_ylim(0.8, 1e4)
ax.set_yscale('log')
ax.set_xscale('log')
ax.set_xlabel('size')
ax.set_ylabel('time relative to {}'.format(baseline)) # you could also use "func.__name__" here instead
ax.grid(which='both')
ax.legend()
plt.tight_layout()
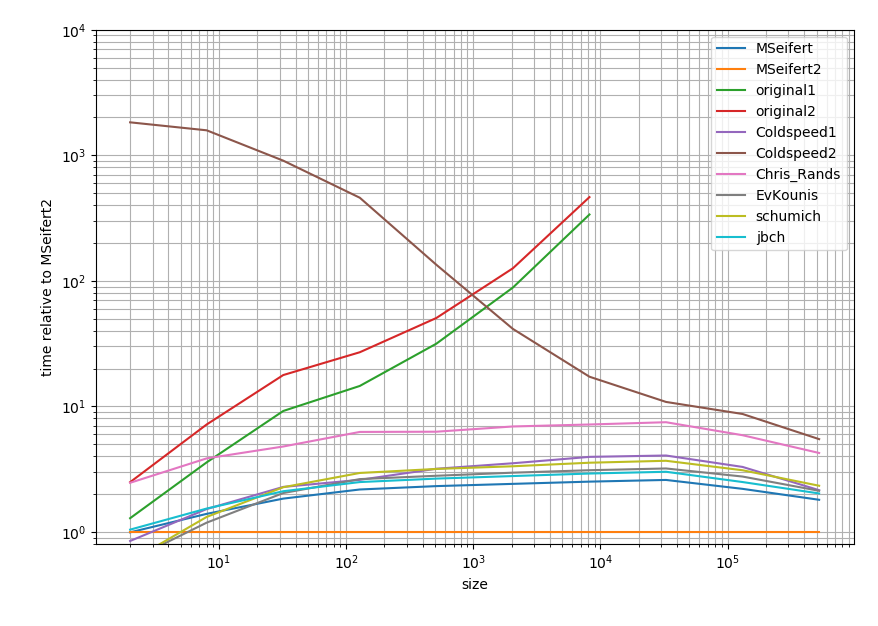
In case you're interested in the exact results I put them in this gist.
![enter image description here]()
It's a log-log plot and relative to the Cython answer. In short: The lower the faster and the range between two major tick represents one order of magnitude.
So all solutions tend to be within one order of magnitude (at least when the list is big) except for the solutions you had. Strangely the pandas solution is quite slow compared to the pure Python approaches. However the Cython solution beats all of the other approaches by a factor of 2.

1s and0s in the original list? – Literatis.groupby(s.ne(s.shift()).cumsum()).cumcount(). – Crossstitch0and start from there, preventing the read-through. However this is python, so you would need to slice it and then multi-process the operation, then combine the list again (python threads are time-sliced within one operating thread. This may take longer than just processing it linearly) – Turgite